Аппендикс 2

Фурье-образ изотропного вихря

Фазовая часть комплексной амплитуды изотропного вихря , записанная в полярных координатах с началом в центре вихря – , а ее модуль – , формируется как произведение:

(А 2.1)

где ограничивающая изотропный вихрь функция зрачка.

Найдем Фурье-образ изотропного вихря.

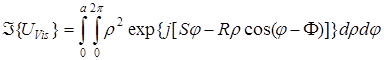, (А 2.2)

где - полярные координаты в частотной плоскости.

Двойной интеграл преобразуется к повторному

(А 2.3)

Внутренний интеграл, обозначим его как 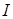, сводится к следующему выражению:

. (А 2.4)

где 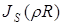– функция Бесселя 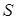-го порядка. Используя известное выражение [111; 112]:

, (А 2.5)

и учитывая, что реально существуют вихри только с единичным топологическим зарядом () уравнение (А 2.4) сводится к виду:

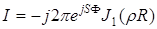. (А 2.6)

Соответственно

. (А 2.7)

Откуда при замене и учитывая, что [111; 112]:

(А 2.8)

вытекает следующее выражение для :

(А 2.9)

Легко показать, что .

Таким образом, Фурье-образом изотропного вихря является также вихревая функция. В области ядра вихря ( невелико), где выполняется соотношение [112]:

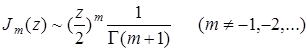(А 2.10)

имеет вид

(А 2.11)

Иными словами, и в частотной области изотропный вихрь фактически не изменяет своей структуры.

Дата добавления: 2015-07-12