Аппендикс 3

вектор Пойнтинга. Параксиальное приближение

Сделаем следующие допущения:

1. Рассматриваемые поля абсолютно когерентны.

2. Распространение волны происходит в свободном пространстве и выполняется параксиальное приближение.

Пусть 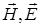– векторы напряженности магнитного и электрического полей. Компоненты этих векторов определяются стандартным образом (см., например, [28]):

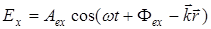
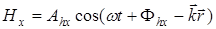и т.д., (A 3.1)

где 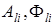(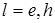, 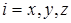) – модули амплитуд и пространственные фазы соответствующих компонент.

Величины 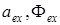…и т.д. – в общем случае функции всех трех координат.

Для параксиального приближения скалярное произведение 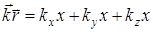за исключением специальных ситуаций (например, поле в области ядра вихря) стремится к 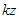. Тогда (A 3.1) преобразуется к виду

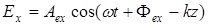и т.д. (A 3.2)

Пусть 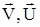– комплексные волновые функции магнитного и электрических полей соответственно. Компоненты этих векторов определяются следующим образом. Например:

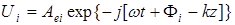, (A 3.3)

где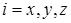

Известно, что имеет место уравнение (см., например, [3]):

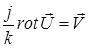, (A 3.4)

где 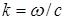– волновое число.

Таким образом, зная 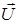, легко выразить комплексную волновую функцию магнитного поля 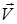через комплексную волновую функцию электрического поля.

Далее, как правило, используя стандартные соотношения для комплексных амплитуд, переходят непосредственно к усредненному по времени значению вектора Умова – Пойнтинга или усредненным моментам импульса электромагнитного поля [100].

В нашем случае, сохраним зависимость от времени и получим соотношения, описывающие мгновенные компоненты вектора Умова – Пойнтинга. С этой целью будем работать с напряженностями полей.

Используя (3. А.4) и тот факт, что 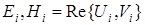, можно показать, что:

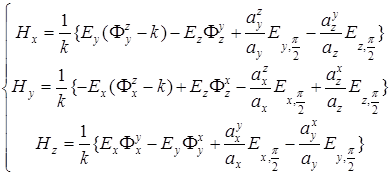(A 3.5)

где 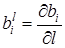; 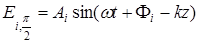– сдвинутая по фазе на 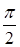соответствующая напряженность электрического поля 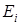. Учитывая, что в дальнейшем мы перейдем только к компонентам электрического поля, здесь и далее величины типа 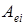будем обозначать просто как .

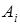Как известно, вектор Пойнтинга описывается соотношением [28]

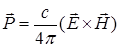(A 3.6)

или для его компонент

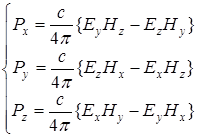. (A 3.7)

Используя (A 3.5 – A 3.7) и исключая все производные по и производные от -компоненты в силу их малости (за исключением членов, содержащих множитель 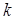( 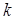велико)), можно получить следующую систему для компонент вектора :

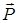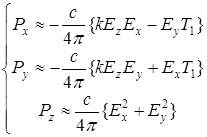, (A 3.8)

где 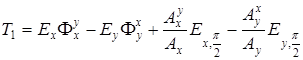и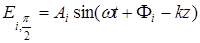

Выразим 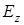через 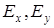. Для этого воспользуемся уравнением, справедливым для свободно распространяющихся волн, записанным для комплексной амплитуды электрического поля:

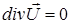или 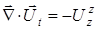, (A 3.9)

где 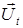– поперечная компонента вектора .

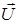Кроме того, будем учитывать, что для параксиального приближения все члены, содержащие производные по , малы, за исключением членов содержащих множитель 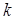. В этом случае справедливо равенство [105]:

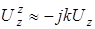. (A 3.10)

Из (A 3.9) и (A 3.10) следует:

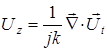. (A 3.11)

Из (A 3.11) имеем:

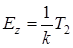, (A 3.12)

где .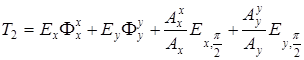

Тогда, с учетом (A 3.12), система (A 3.8) перепишется в виде:

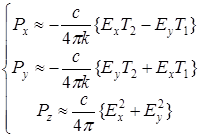, (A 3.13)

где

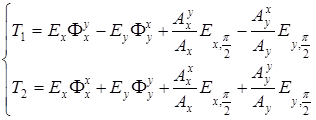. (A 3.14)

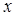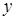Таким образом, при выполнении параксиального приближения соотношения для мгновенных компонент вектора Умова – Пойнтинга могут быть записаны в терминах характеристик только - и -компонент электрического поля.

Модуль поперечной составляющей вектора Умова – Пойнтинга соответственно запишется:

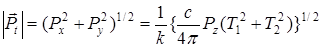. (A 3.15

Ориентация поперечной составляющей задается отношением .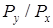

Соответственно направление составляющей вектора Умова – Пойнтинга в плоскости 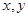определяется значением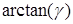

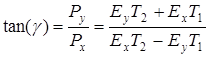. (A 3.16)

Список Литературы

1. Франсон M. Оптика спеклов. – М.: Мир, 1980.

2. Гудмен Дж. Статистическая оптика. – М.: Мир, 1988.

3. Nye J.F. Natural focusing and fine structure of light. Institute of physics publishing, Bristol and Philadelphia, 1999.

4. Nye J.F., Berry M. Dislocations in wave trains. Proc. R. Soc. Lond., A 336, P. 165-190, 1974

5. Berry M.V. Singularities in waves and rays. Physics of defects. Les Houches Session XXXV, 28 July - 29, August 1980, Amsterdam: North-Holland., P. 453-543, 1981

6. Reference List on Singular Optics, Swartzlander G., Jr., http://www.u.arizona.edu/~grovers/SO/.

7. Nye J.F. The Motion and structure of dislocations in wave fronts. Proc. R. Soc. Lond., A 378, P. 219-239, 1981.

8. Баранова Н.Б., Зельдович Б.Я. Дислокации поверхности волнового фронта и нули амплитуды. ЖЭТФ, 80,. 5, С. 1789-1797, 1981.

9. Баранова Н.Б., Зельдович Б.Я., Мамаев А.В., Пилипецкий Н.Ф., Шкунов В.В. Исследование плотности дислокаций волнового фронта световых полей. ЖЭТФ, 83, 5, С. 1702-1710, 1982.

10. Baranova N.B., Mamayev A.V., Pilipetsky N.F., Shkunov V.V., Zeldovich B.Ya. Wavefront dislocations: topological limitations for adaptive systems with phase conjugation. J.Opt.Soc.Am, A73, P. 525-528, 1983.

11. Nye J.F., F.R.S., Hajnal J.V., Hannay J.H. Phase saddles and dislocations in two-dimensional waves such as the tides. Proc. R. Soc. Lond., A 417, P. 7-20, 1988.

12. Freund I., Shvartsman N., Freilikher V. Optical dislocation networks in highly random media. Opt. Comm., 101, P. 247-264, 1993.

13. Freund I., Shvartsman N. Wave-field singularities: The sign principle. Phys. Rev. 50 (6),.P. 5164-5172, 1994.

14. Optical vortices. Horizons in world physics. V. 228. Edited by M. Vasnetsov, K. Stliunas. Nova Science Publ. 1999.

15. Berry M.V., Nye J.F., Wright F.J. The elliptic umbilic diffraction catastrophe. Proc. R. Soc. Lond., A 291, pp. 453-484, 1979.

16. Vaupel M., Weiss C.O. Circling optical vortices. Phys. Rev. A, 51, pp. 4078-4085, 1995.

17. Freund I. Saddles, singularities, and extrema in a random-phase fields. Phys.Rev. E52, P. 2348-2360, 1995.

18. Shvartsman N., Freund I. Speckle spots ride phase saddles sidesaddle. Opt. Comm., 117, 228-234, 1995.

19. Freund I. Critical-point level-crossing geometry in wave fields. J.Opt.Soc.Am., A14, P. 1911-1927, 1997.

20. Freund I. ‘1001’ correlations in random wave fields. Waves Random Media,. 8,. P. 119-158, 1998.

21. Freund I., Shvartsman N.. Vortices in Random Wave Fields: Nearest Neibor Anticorrelations. Physical Review Letters, 72, P. 1008-1011, 1994.

22. Freund I. Amplitude topological singularities in random electromagnetic wavefields. Phys. Lett. A. 198, pp.139-144, 1995.

23. Freund I. Vortex derivatives. Opt. Comm., 137, pp. 118-126, 1997.

24. Freund I. Optical phase maps. SPIE Proc., 2389, pp. 411-419, 1995.

25. Mokhun I. Amplitude zeroes and structure of statistical optical fields. Correlation between the field’s intensity and phase. Proc. SPIE, 3573,. P. 567-571, 1998.

26. Ангельський О.В., Бесага Р.М., Ковальчук О.В., Мохунь І.І. Структура статистичних скалярних полів // Наук. Вісн. Чернівецького унів.,Вип. 66, Фізика. Електроніка. – С.66-68, 1999.

27. Freund I., Freilikher V. Parameterization of anisotropic vortices. JOSA A, 14, 1902-1910, 1997.

28. Борн М., Вольф Э. Основы оптики / Пер. с англ. – М.: Наука, – 1973.

29. Indebetouw G. Optical vortices and their propagation. J. of Mod. Opt., 40, P. 73-87, 1999.

30. Heckenberg N.R., McDuff R., Smith C.P., Rubinsztein-Dunlop H., Wegener M.J. Laser beams with phase singularities. Opt. & Quant. Electr., 24, P. S951-S962, 1992.

31. Heckenberg N.R., Vaupel M., Malos J.T., Weiss C.O. Optical-vortex pair creation and annihilation and helical astigmatism of a nonplanar ring resonator. Phys. Rev. A, 54, P. 2369-2378, 1996.

32. Berry M.V. Much ado about nothing: optical dislocation lines (phase singularities, zeroes, vortices…). Proc. SPIE., 3487, P. 1-5,1998.

33. Berry M.V. Wave dislocation reactions in non-paraxial Gaussian beams. J.Mod.Opt., 45, P. 1845-1858 1998.

34. Abramochkin E., Volostnikov V. Spiral-beams: optical and quantum aspects. Opt. Comm., 125, P. 302-323, 1996.

35. Abramochkin E., Volostnikov V. Structurally stable singular wavefields. Proc. SPIE, 3487, pp. 20-28, 1998.

36. White A.G., Smith C.P., Heckenberg N.R., Rubinsztein-Dunlop H., McDuff R., Weiss C.O. Interferometric measurements of phase singularities in the output of a visible laser. J. Mod. Opt., 38, P. 2531-2541, 1991.

37. Basisty I.V., Soskin M.S., Vasnetsov M.V. Optical wavefront dislocations and their properties. Opt. Comm., 119, P. 604-612, 1995.

38. Soskin M.S., Vasnetsov M.V., Basisty I.V. Optical wavefront dislocations. Proc. SPIE, 2647, P. 57-62, 1995.

39. Heckenberg N.R., McDuff R., Smith C.P. and White A.G. Generation of optical singularities by computer-generated holograms. Opt. Lett., 17, P. 221-223, 1992.

40. Рытов С.М., Кравцов Ю.А., Татарский В.И. Введение в статистическую радиофизику. – Ч2. – М.: Наука, 1978.

41. Freund I. Optical vortex trajectories, Opt. Comm., 181 pp. 19-33, 2000.

42. Rozas D., Law C.T., Swartzlander G.A. Propagation dynamics of optical vortices. JOSA B, 14, pp. 3054-3065, 1997.

43. Rozas D., Sacks Z.S., Swartzlander G.A. Experimental observation of fluidlike motion of optical vortices Phys. Rev. Lett., 79 pp. 3399-3402, 1997.

44. Розанов Н.Н. О формировании излучения с дислокациями волнового фронта // Оптика и спектроскопия, 75, 1993, С. 861-867.

45. Nicholls K.W., Nye J.F. Three-beam model for studying dislocations in wave pulses, Journ. of Phys. A Mathem. & General, 20, pp. 4673-4696, 1987.

46. Masajada J., Dubik B. Optical vortex generation by three plane wave interference, Opt. Comm., 198, pp. 21-27, 2001.

47. Angelsky O.V., Besaha R.N., Mokhun I.I. Appearance of wave front dislocations under interference among beams with simple wave fronts. Optica Aplicata, XXVII, (4), P. 273-278, 1997.

48. Angelsky, R.Besaha, I.Mokhun. Appearance of wave front dislocations under interference among beams with simple wave fronts. SPIE Proc., 3317, P. 97-100, 1997.

49. Nye J.F. Unfolding of higher-order wave dislocations J.Opt.Soc.Am., A 15, P. 1132 – 1138, 1998.

50. Karman G.P., Duijl A. van, and Woerdman J.P. Unfolding of an unstable singularity into a ring. Opt.Lett., 23, p.403-405, 1998.

51. Karman G.P., Woerdman J.P. How phase and amplitude aberration destabilized the phase singularities. J.Opt.Soc.Am., A 15, p. 2862 – 2868, 1998.

52. Lukin V.P.,. Sennikov V.A, Tartakovski V.A. Optical vortices: creation, annihilation, and modeling. Proc. SPIE, 4724, pp. 85-93, 2002.

53. Ангельський О.В., Бесага Р.М., Коновчук О.В., Мохунь І.І. Отримання вихрових пучків. Наук. Вісн. Чернівецького унів., Вип. 79, Фізика. Електроніка, С. 40-42, 2000.

54. Mandel L., Wolf E. Optical coherence and quantum optics. Cambridge university press, 1995.

55. Arecchi F.T., Giacomelli G., Ramazza P.L., Residori S. Vortices and defect statistics in two-dimensional optical chaos Phys. Rev. Lett. 67, 3749-3752, 1991.

56. Zuravlev V.A., Kobozev I.K., Kravtsov Yu.A. Statistical characteristics of phase front dislocations of a wave field, JETP, 75, pp. 256-262, 1992.

57. Freund I. Optical vortices in Gaussian random wave fields: statistical probability densities. JOSA A, 11 pp. 1644-1652, 1994.

58. Arsenyan T.I., Embaukhov S., Fedotov N., Korolenko P., Petrova G. Statistical characteristics of light fields with helical dislocations of the wave front. Proc. SPIE, 3487, pp. 148-155, 1998.

59. Макс Ж. Методы и техника обработки сигналов при физических измерениях. Т. 1 – М.: Мир. 1983.

60. Angelsky O., Brandel R., Mokhun I. Characteristics of scalar random field and its vortex networks. Recovery of the optical phase. SPIE Proc., 4607, P. 25-29, 2002.

61. Обратные задачи в оптике / Под ред. Г. П. Болтса – М.: Машиностроение, 1984.

62. Аблеков В.К., Зубков Б.И., Фролов А.В. Оптическая и оптоэлектронная обработка информации. – М.: Машиностроение, 1976.

63. Аблеков В.К., Колядин С.А., Фролов А.В. Высокоразрешающие оптические системы. – М.: Машиностроение. 1985.

64. Nye J.F. Line singularities in wave fields. Phil. Trans. R. Soc. Lond., A 355, P. 2065-2069, 1997.

65. Nye J.F. Polarization effects in the diffraction of electromagnetic waves: the role of disclinations. Proc. R. Soc. Lond., A 387, P. 105-132, 1983.

66. Nye J.F. Lines of circular polarization in electromagnetic wave fields. Proc. R. Soc. Lond., A 389, P. 279-290, 1983.

67. A.I. Konukhov, L.A. Melnikov. Optical vortices in a vector field: the general definition based on the analogy with topological solitons in a 2D ferromagnet, and examples from the polarization transverse patterns in a laser. J. Opt. B: Quantum Semiclass. Opt. 3, S139–S144, 2001.

68. Angelsky O.V., Besaha R.N., Mokhun I.I., Sopin M.O. About thin structure of speckle field. SPIE Proc., 2647, P. 75-79, 1995.

69. Angelsky O.V., Besaha R.N., Mokhun I.I., Sopin M.O. About thin structure of speckle field. SPIE Proc., 2778, P. 357-358, 1996.

70. Angelsky O., Besaha R., Mokhun I.. Study of statistical fields in vicinity of zero-crossing. SPIE Proc., 3317, P. 88-96, 1997.

71. Ангельский О.В., Бесага Р.Н., Мохунь И.И. О тонкой структуре спекл поля в областях малых амплитуд // Оптика и спектроскопия, 82, 1997, С. 621-629.

72. Mokhun I., Sopin M. Thin structure of coherent optical fields in the vicinity of minimal intensity and its connection with wave front dislocations. SPIE Proc., 3317, P. 108-110, 1997.

73. Nye J.F., Hajnal J.V. The wave structure of monochromatic electromagnetic radiation. Proc. R. Soc. Lond., A 409, P. 21-36, 1987.

74. Apostol A., Dogariu A. First- and second-order statistics of optical near fields. Opt Lett., 29, pp. 235-237, 2004.

75. Ellis J., Dogariu A. Discrimination of globally unpolarized fields through Stokes vector element correlations. J. Opt. Soc. Am A, 22, pp. 491-496 2005.

76. Dogariu A,. Wolf E. Coherence theory of pairs of correlated wave fields. Journ. of Modern Opt., 50, 1791-1796, 2003.

77. Hajnal J.V. Singularities in the transverse fields of electromagnetic waves I. Theory. Proc. R. Soc. Lond., A 414, P. 433-446, 1987.

78. Hajnal J.V. Singularities in the transverse fields of electromagnetic waves II. Proc. R. Soc. Lond., A 414, P. 447-468, 1987.

79. Hajnal J.V. Observation of singularities in the electric and magnetic fields of freely propagating microwaves. Proc. R. Soc. Lond., A 430, P. 447-468, 1987.

80. Аззам Р., Башара Н. Эллипсометрия и поляризованный свет. – М.: Мир, 1981.

81. Angelsky O., Mokhun A., Mokhun I., Soskin M. The relationship between topological characteristics of component vortices and polarization singularities. Opt. Comm., 207, P. 57-65, 2002.

82. Angelsky O., Besaha R., Mokhun A., Mokhun I., Sopin M., Soskin M., Vasnetsov M. Singularities in vectoral fields. SPIE Proc., 3904, P. 40 – 55, 1999.

83. Ангельський О.В., Бесага Р.М., Мохунь І.І. Сопин М.О., Соскін М.С. Сингулярності у векторних полях // Наук. Вісн. Чернівецького унів., Вип. 57, Фізика, С.88 – 99, 1999.

84. Angelsky O.V., Mokhun I.I, Mokhun A.I, Soskin M.S. Interferometric methods in diagnostics of polarization singularities. Phys. Rev. E., 65, 036602(5), 2002.

85. Angelsky O.V., Mokhun I.I, Mokhun A.I, Soskin M.S. Inerferometric Methods in diagnostics of polarization singularities. SPIE Proc., 4829, Р.487-488, 2002.

86. Mokhun A.I., Soskin M.S., Freund I. Elliptic critical points: C-points, a-lines, and the sign rule. Opt. Lett., 27, pp. 995-997, 2002.

87. Freund I., Soskin M.S., Mokhun A.I. Elliptic critical points in paraxial optical fields. Opt. Commun., 207, P. 223-253, 2002.

88. Fruend I. Second harmonic generation of optical ellipse fields. Opt. Comm., 213, P. 129-149, 2002.

89. Freund I. Polarization singularity indices in Gaussian laser beams. Opt. Comm., 201, P. 251-270, 2002.

90. Ангельський О.В., Бесага Р.М., Мохунь А.І., Мохунь І.І., Соскін М.С. Елементарні поляризаційні сингулярності // Наук. Вісн. Чернівецького унів., 63: Фізика. Електроніка., С.45-51, 1999.

91. Ван-де-Хюлст Г. Рассеяние света малыми частицами. – М.: Энергия, 1987.

92. Мировицкий Д.И., Будагян И.Ф., Дубровин В.Ф. Микроволноводная оптика и голография. – М.: Наука, 1983.

93. Абезгауз Г.Г., Тронь А.П., Копенкин Ю.Н., Коровина И.А. Справочник по вероятностным расчетам. – М.: Воениздат, 1970.

94. Папулис А. Теория систем и преобразований в оптике. – М.: Мир, 1971.

95. Nieto-Vesperinas M. Scattering and Diffraction in Physical Optics. A Wiley-Interscience Publication, John Wiley and suns, Inc., 1981.

96. Brandel R., Mokhun A., Mokhun I., Viktorovskaya Ju. Fine structure of inhomogeneous vector field and his space averaged polarization characteristics. Optica Applicata, 36, pp 75-95, 2006.

97. Brandel R., Mokhun A., Mokhun I., Viktorovskaya Ju. Space averaged polarization characteristics of inhomogeneous vector field. Proc. SPIE, 5972, pp. 38-45, 2005.

98. Freund I., Mokhun A.I., Soskin M.S., Angelsky O.V., Mokhun I.I. Stokes singularity relations. Opt. Lett., 27, P.545-547, 2002.

99. Freund I. Polarization flowers. Optics Comm., 199, pp. 47-63, 2001.

100. Allen L., Padgett M.J. and Babiker M. The orbital angular momentum of light. E.Wolf, Progress in optics XXXIX 1999, Elsevier Science B.V.

101. Allen L., Padgett M.J. The Poynting vector in Laguerre-Gaussian beams and the interpretation of their angular momentum density. Opt. Comm., 184, pp. 67 71, 2000.

102. He H., Friese M.E.J., Heckenberg N.R., Rubinsztein-Dunlop H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Letters, 75, pp. 826-829, 1995.

103. Gahagan K.N., Swartzlander G.A. Optical vortex trapping of particles. Opt. Lett., 21, pp. 827-829, 1999.

104. Matthew J.Lang, Steven M. Block. “Resource Letter: LBOT-1: Laser-based optical tweezers”. Am. J. Phys., 71, pp. 201-215, 2003.

105. Berry M. Paraxial beams of spinning light, Proc. SPIE, 3487, pp. 6-11, 1998.

106. Arnold V.I. Catastrophe Theory. Second revised and expended edition Berlin, Springer, 1986.

107. Mokhun I., Arkhelyuk A., Brandel R. Viktorovskaya Ju. Angular momentum of electromagnetic field in areas of optical singularities. SPIE Proc., 5477, pp. 47-54, 2004.

Дата добавления: 2015-07-12