
|
Читайте также: |
& Литература: [1], [2], [8], [7].
Линейным гармоническим осциллятором называют систему, описываемую гамильтонианом  =
=  +
+  . (21.1)
. (21.1)
При решении стационарного уравнения Шредингера
 Y = E Y (21.2)
Y = E Y (21.2)
используют безразмерные переменные
λ=  и z = x
и z = x  . (21.3)
. (21.3)
Получается  + (l – z2) Y. (21.2)
+ (l – z2) Y. (21.2)
Решение ищется в виде Y = exp (–  )
)  . (21.4)
. (21.4)
Такая функция удовлетворяет уравнению (21.2), если коэффициенты ряда подчиняются рекуррентному соотношению
a k+2 = a k  (21.5)
(21.5)
Исследование функции (21.4) показывает, что она конечна только в том случае, если ряд, входящий в ее выражение, фактически представляет собой полином. Ряд станет полиномом, если числитель в формуле (21.5) обратится в нуль при k = n, то есть если величина λ, будет удовлетворять условию 2 n + 1 – λ = 0. (21.6)
Этому λ соответствует некоторое E (см. (21.3)). Так получается формула, определяющая энергетический спектр гармонического осциллятора:
E = ħ ω (n + 1 / 2), где n = 0, 1, 2, …. (21.7)
Волновая функция осциллятора (21.4) при подстановке (21.5) и (21.6) принимает вид Yn = Nn exp (–  ) Hn(z), (21.8)
) Hn(z), (21.8)
где Nn – нормирующий множитель, а Hn(z) – полином Чебышева – Эрмита n-ой степени.
Анализ волновых функций при различных n приводят к следующим заключениям:
§ четным квантовым числам n соответствуют четные волновые функции, нечетным n – нечетные;
§ волновые функции имеют n узлов и отличны от нуля за точками остановки аналогичного классического осциллятора;
§ при n ® ¥ распределение плотности вероятности нахождения частицы в точке x в среднем оказывается таким же, как и для классического осциллятора, что подтверждает принцип соответствия.
? Контрольные вопросы
1. Какие системы моделирует задача о линейном гармоническом осцилляторе?
2. Расскажите о последовательных этапах решения стационарного уравнения Шредингера для гармонического осциллятора.
3. Назовите основные положения, которые используются при нахождении энергетического спектра линейного гармонического осциллятора.
4. Расскажите об энергетическом спектре гармонического осциллятора. Сравните с формулой Планка.
5. Расскажите о волновой функции осциллятора.
6. Сравните поведение классического и квантово-механического осцилляторов.
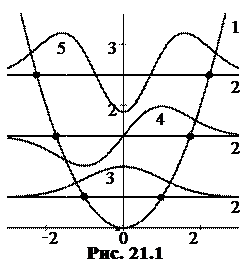
|
22.1 Получите стационарное уравнение для гармонического осциллятора в безразмерных переменных и найдите его решение при x ® ¥.
22.2 Получите рекуррентное соотношение (21.5).
22.3 Покажите, что ряд, входящий в формулу (21.4), стремится к
exp (z2). Как этот факт используется при нахождении энергетического спектра осциллятора?
22.4 Гармонический осциллятор помещается в постоянное электрическое поле. Как это сказывается на его энергетическом спектре и на волновых функциях?
22.5 На рисунке 21.1 изображены графики, иллюстрирующие свойства линейного гармонического осциллятора. Какой смысл имеют линии 1, 2, 3, 4, 5? Чем замечательны отмеченные на рисунке 21.1 точки? Как зависит энергия нулевых колебаний и разность энергетических уровней от параметра, определяющего потенциальную функцию? При каких квантовых числах n Y-функции четная? Сколько узлов имеет Y-функция? Сравните распределение плотности вероятности обнаружить частицу в точке x для квантового и для классического осцилляторов при малых n и при n ® ¥.
Дата добавления: 2015-07-11; просмотров: 269 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Прохождение частицы через потенциальный барьер. Туннельный эффект | | | Ротатор. Собственные функции и собственные значения операторов орбитального момента импульса |