Свободное движение микрочастиц

& Литература: [1], [2], [7], [8].

В этой главе рассматриваются системы, гамильтониан которых не зависит от времени. Для таких систем имеет смысл исследование стационарных состояний. Временная часть волновой функции всех стационарных состояний имеет одинаковый вид (смотри (14.9)). Поэтому задача сводится к решению стационарного уравнения Шредингера (14.10). Здесь используется координатное представление, так что (14.10) принимает вид

Y() = E Y(). (18.1)

Задача о нахождении собственных функций Y() и собственных значений E гамильтониана (18.1) упрощается благодаря теореме о разделении переменных.

Если гамильтониан системы равен сумме независимых частей:

= ₁(x₁) + ₂(x₂), (18.2)

то его собственное значение E равно сумме собственных значений этих частей: E = E₁ + E₂, (18.3)

а собственная функция Y равна произведению собственных функций слагаемых гамильтонианов: Y = Y₁(x₁) Y₂(x₂). (18.4)

Под свободным движением подразумевается движение частицы, потенциальная энергия которой во внешнем поле не зависит от радиус-вектора: U() = const. В этом случае благодаря теореме о разделении переменных уравнение (18.1) сводится к уравнению с одной переменной:

+ (E – U) Y = 0. (18.5)

Решением этого уравнения является функция

Y = A exp(i k x) + B exp(–i k x), (18.6)

где k = . (18.7)

Произвольные постоянные A и B должны обеспечивать непрерывность, однозначность и конечность функции Y. Этим стандартным условиям волновая функция удовлетворяет всегда. Можно показать также, что производная Y-функции непрерывна во всех точках, в которых потенциальная функция U(x) не испытывает бесконечных скачков.

Если E ³ U, то функция (18.6) представляет собой волну де Бройля.

Полученные для свободного движения результаты позволяют сделать важные выводы, относящиеся к типичным ситуациям, для которых потенциальная функция имеет вид, показанный на рисунке 18.1.

При координате x, стремящейся к бесконечности, функция U(x) стремится к нулю. Так что достаточно далеко от начала координат движение частицы можно считать свободным.

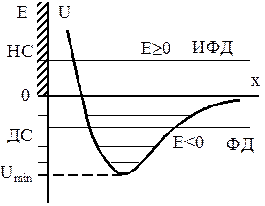Рис. 18.1

Если Е ³ 0, то волновая функция в области x ® ¥ принимает вид волны де Бройля, и поэтому при x ® ¥ величина |Y|² ® const ¹ 0. Движение, для которого |Y|² ¹ 0 при x ® ¥ называют инфинитным (ИФД). Импульс и энергия частицы, описываемой волной де Бройля, имеют непрерывный спектр (НС), что отражено на рисунке 18.1.

Если E < 0, то для обеспечения конечности Y-функции (18.6) при x ® ¥ необходимо положить B = 0. Тогда

Y ® A exp(–|k| x) Þ |Y|² ® 0,

и квадрат нормы функции N= = + ¹ ¥, так как ® 0 при x ® ¥.

Движение, для которого ® 0 при x ® ¥, называют финитным (ФД). Поскольку для рассматриваемого финитного движения N ¹ ¥, Y-функцию можно нормировать на единицу. Поэтому условие ортонормированности собственных векторов |E> гамильтониана должно быть выражено не через d-функцию, а через символ Кронекера: <E_i|E_j> = d_ij. Последнее означает, что энергия E имеет дискретный спектр (ДС) (рис.18.1).

Из формулы для среднего значения энергии <E> = <p²>/(2 m) + <U> видно, что <E> > U_min, где U_min – минимальное значение потенциальной функции. Вот почему энергетические уровни располагаются выше этого значения (рис.18.1).

? Контрольные вопросы

1. Почему в ряде случаев решают только стационарное уравнение Шредингера, а не полное?

2. Сформулируйте теорему о разделении переменных в уравнении Шредингера.

3. Что такое свободное движение и какой для него вид имеет волновая функция?

4. Расскажите об инфинитном движении и о характерном для него виде энергетического спектра.

5. Расскажите о финитном движении и о характерном для него виде энергетического спектра.

F

Задания

21.1 Докажите теорему о разделении переменных в уравнении Шредингера.

21.2 Докажите теорему о непрерывности производной волновой функции.

Дата добавления: 2015-07-11