Уравнение движения в форме Гейзенберга. Интегралы движения

& Литература: [1], [3].

Уравнения движения в форме Гейзенберга позволяют судить об изменении той или иной величины непосредственно, без предварительного нахождения амплитуды состояния. Они учитывают то обстоятельство, что представляющая интерес величина может вообще не иметь определенного значения. Поэтому с их помощью находится изменение со временем среднего значения величины.

Вводится оператор Û производной величины F по времени такой, что для любого состояния |Y>

< > Û <Y| |Y> = <F> Û <Y| |Y>. (15.1)

Именно этот оператор и удовлетворяет уравнению движения в форме Гейзенберга: = = 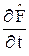+ { , }, (15.2)

где { , } = [ , ] = [ – ] – (15.3)

квантовые скобки Пуассона.

Уравнение (15.2) отражает то обстоятельство, что изменение среднего значения <F> величины F может происходить вследствие изменения со временем вида самого оператора, а также вследствие перераспределения величины F по ее возможным значениям.

Величина F, для которой = 0, называется интегралом движения.

Для того чтобы величина F была интегралом движения, достаточно, чтобы ее оператор явно не зависел от времени и чтобы он коммутировал с оператором Гамильтона.

? Контрольные вопросы

1. Что имеют общего и чем отличаются друг от друга уравнения движения в форме Шредингера и в форме Гейзенберга?

2. Какой смысл имеет оператор производной физической величины по времени?

3. Какой смысл имеет каждое слагаемое в правой части уравнения (15.2)?

4. Что имеют общего и чем отличаются друг от друга интегралы движения в квантовой механике и в классической физике?

5. Как узнать, является ли та или иная величина в определенных условиях интегралом движения или нет? Приведите примеры.

F

Задания

17.1. Докажите следующие операторные равенства:

( + ) = + ; ( ) = + .

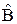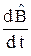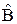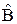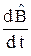17.2. Какие из механических величин (E, P_x, P_y P_z) сохраняются при движении частицы: а) в отсутствии поля; б) в поле с потенциальной функцией U = a z?

17.3. Покажите, что в центральном поле квадрат момента импульса L² и его проекция L_z являются интегралами движения. Оператор 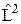в сферических координатах имеет вид (22.3), а 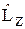= – i ħ .

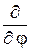Дата добавления: 2015-07-11