Состояния микрочастиц

& Литература: [8], [7], [9] [11].

Физические теории строятся по аналогии с классической механикой, не даром она называется классической. Естественно, теория должна отражать специфику описываемых объектов.

Классическая теория оперирует понятием состояния рассматриваемой системы. Состояние классической частицы задано, если указаны радиус-вектор 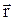и импульс 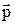частицы. Для задания состояния системы частиц нужно задать совокупность обобщенных координат и обобщенных импульсов. Указанная информация позволяет найти все остальные величины, например, момент импульса, кинетическую и потенциальную энергии, а также найти значения всех величин в любой последующий момент времени.

Аналогично для задания состояния микрообъекта необходима полная информация о результатах измерения любой величины в данный момент времени. Задавать состояние произвольными значениями некоторых величин, как это делается в классической физике, для микрочастиц оказывается неприемлемым по ряду причин.

Величины, характеризующие микрочастицы, могут принимать дискретные значения – квантуются. Вообще говоря, эти величины могут иметь и дискретный спектр значений, и непрерывный, и смешанный. Например, энергия электрона в поле атомного ядра принимает дискретный ряд значений, если она меньше энергии связи с ядром, и может принимать любое значение, большее энергии связи.

Еще одной особенностью микрочастиц является наличие величин, не имеющих определенного значения в одном состоянии. Примером таких величин являются координата x и проекция импульса p_x, связанные соотношением неопределенности Гейзенберга (4.2). Величины, которые не могут иметь определенных значений в одном состоянии, называют несовместными. Величины называют совместно измеримыми (совместными), если в состоянии с определенным значением одной из них остальные также имеют определенные значения. Совокупность независимых совместных величин, через которые может быть найдена любая другая совместная с ними величина, называется полным набором.

Задав значения величин полного набора с учетом их спектра, мы укажем на конкретное состояние, но этого не достаточно для его описания, поскольку нет никакой информации о величинах, не входящих в полный набор.

Следует учесть еще одну специфику микрочастиц – их вероятностное поведение. Детальный анализ этой особенности позволяет найти адекватный способ описания их состояния.

Обратимся к мысленному эксперименту Р. Фейнмана по дифракции электронов на двух щелях. Электрон вылетает из источника s, проходит через две щели (1 и 2) и регистрируется детектором D в точке с координатой x (рис 5.1). Размерами детектора пренебрегаем. Показания детектора W пропорциональны вероятности попадания в него электрона. Если открыта только одна из щелей, то зависимость показаний детектора от его координаты имеет вид W₁ или W₂, а если открыты обе щели – то W (рис. 5.2).

Если бы аналогичный опыт проводился с пулями (корпускулами), то каждая пуля, пролетев через одну из щелей, попала бы в некоторую точку экрана. Координата этой точки – случайная величина. Но вероятности попадания в те или иные точки обнаруживают определенную закономерность. В этом отношении вероятностное поведение электронов не отличается от поведения корпускул.

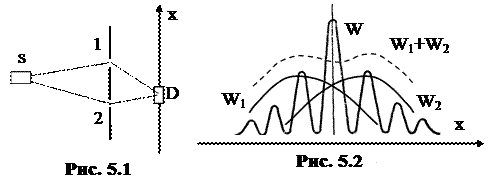При одной открытой щели функции W₁(x) и W₂(x) имеют одинаковый вид как для электронов, так и для корпускул, но когда обе щели открыты, получаются качественно различные картины. Для корпускул наблюдается сумма функций W₁(x) + W₂(x), чего и следовало ожидать, опираясь на теорию вероятности. Для электронов же получается функция W(x), аналогичная распределению интенсивности волн при интерференции на двух щелях. Именно эту специфическую особенность имеют в виду, когда говорят о вероятностном поведении микрочастиц.

Такое поведение микрочастиц с точки зрения привычных (классических) представлений выглядит совершенно непонятным. Интерференция волны возникает из-за того, что она проходит через оба отверстия, ее колебания складываются в каждой точке экрана с учетом разности расстояний от каждой щели. Интенсивность суммарных колебаний и образует интерференционную картину. Электрон не проходит через обе щели сразу и целиком регистрируется детектором, он не делим. Интерференционная картина присуща вероятности попадания электронов в различные точки экрана. Эту суть вероятностного поведения микрочастиц следует учесть при описании их состояний.

При описании интерференции волн сначала складывают колебания, а затем находят их интенсивности. Гармонические колебания описывают комплексными функциями Y = A exp(– i (w t – 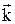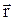)), которые называют амплитудами колебаний. Интенсивность колебания пропорциональна квадрату модуля амплитуды: I ~ úYç² = Y^*Y. Поскольку для микрочастиц вероятности W(x) аналогичны интенсивностям волн I(x), для отображения вероятностного поведения частиц следует использовать комплексные величины áxïYñ, аналогичные амплитудам волн Y(x). Подобно тому, как интенсивность I ~ úYç², вероятность W(x) ~úáxïYñç². Число áxïYñ называют амплитудой вероятности того, что частица находится в точке x. Символ Y здесь обозначает рассматриваемую ситуацию. В мысленном эксперименте с двумя щелями вместо этого символа удобнее использовать символ s. Тогда áxïsñ – амплитуда вероятности того, что электрон попал в точку x экрана, вылетев из источника s. Интерференцию вероятностей в рассмотренном опыте можно описать выражением:

W(x) ~ úáxïsñç² = úáxïsñ₁ + áxïsñ₂ç², (5.1)

áxïsñ_i – амплитуда вероятности того, что электрон, вылетевший из источника s, попал в точку x через i-ю щель.

Полная информация о поведении электрона в рассмотренной ситуации предполагает знание амплитуд вероятностей для всех точек x экрана. Поэтому именно эта совокупность áxïsñ и описывает состояние электрона. Ее называют амплитудой состояния. Если размерами детектора можно пренебречь, то амплитуда состояния представляет собой непрерывную функцию Y(x) = áxïsñ – волновую функцию (Y-функцию). Первым, кто догадался описывать состояние микрочастиц посредством Y-функций, был М. Борн.

Перейдем от рассмотренного мысленного эксперимента к общему случаю. Пусть аналогично координате x интерес представляют величины B_i, входящие в полный набор переменных {B₁, B₂,…B_i}, который будем обозначать одной буквой B. Тогда состояние микрообъекта s описывается совокупностью амплитуд вероятности áBïsñ. Эту совокупность называют амплитудой состояния s в B-представлении. Если величины набора B имеют непрерывный спектр значений, то амплитуда состояния представляет собой волновую функцию от переменных B: áBïsñ = Y_s(B).

Вместо символа s, обозначающего рассматриваемое состояние, можно указать переменные A, образующие в этом состоянии полный набор. Тогда áBïAñ при всевозможных значениях B есть амплитуда состояния A в B-представлении. Символ A – символ состояния, символ B – символ представления. Вероятность определенных значений набора B в данном состоянии A пропорциональна квадрату модуля числа áBïAñ. Чтобы экспериментально измерить эту вероятность, следует вначале создать состояние A (зафиксировать переменные A), а затем провести измерения для определенных значений B. Набор этих значений определяет состояние B. Так что величина ÷áBïAñç² пропорциональна вероятности перехода в состояние B из состояния A. Поэтому амплитуду áBïAñ при фиксированных значениях переменных называют амплитудой перехода в состояние B из состояния A.

? Контрольные вопросы

1. Что понимают под состоянием какой-либо системы?

2. Как задается состояние частицы и состояние системы частиц в классической физике?

3. Почему классический способ описания состояний не годится для микрообъектов?

4. Расскажите о совместных и не совместных величинах.

5. Что такое полный набор? Что общего он имеет с совокупностью обобщенных координат и импульсов в классической физике и чем от нее отличается?

6. Чем поведение электронов в опыте с двумя щелями напоминает поведение корпускул и чем отличается от него?

7. Чем поведение электронов в опыте с двумя щелями напоминает поведение волн и чем отличается от него?

8. В чем проявляется вероятностное поведение электронов в опыте с двумя щелями?

9. Что такое амплитуда волны?

10. Что такое амплитуда вероятности? Как она позволяет описать вероятностное поведение электрона в опыте с двумя щелями?

11. Что такое амплитуда состояния? Что такое волновая функция?

12. Почему амплитуду áBïAñ называют амплитудой перехода?

Дата добавления: 2015-07-11