Матричное и координатное представления

& Литература: [8], [3], [7].

Как отмечалось, векторный формализм удобен в теории, а для получения результатов, подлежащих измерениям, следует использовать различные представления. В классической физике векторные величины представляют их проекциями. В квантовой механике от векторов состояния переходят к амплитудам в различных представлениях. Базисом представления может быть совокупность векторов ÷bñ какого-либо квантово-механического оператора 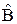(B-представление).

Пусть базис образует счетное множество векторов: ÷bñ = ÷kñ, где k = 1, 2, … Тогда произвольный вектор состояния можно представить в виде:

÷Yñ = = , (10.1)

где Y_k = – амплитуда состояния Y. Она представляет собой множество чисел, которое отображают матрицей-столбцом. Здесь и далее суммирование подразумевается по дважды повторяющимся индексам.

В сопряженном пространстве состояние Y описывается bra-вектором

÷Yñ⁺ = áYç = 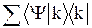= , (10.2)

где Y_k⁺ = = Y_k*. Это множество чисел отображают матрицей-строкой.

Применив к вектору состояния ÷Yñ некоторый оператор , получим другой вектор ÷jñ, который тоже может быть разложен по базису ÷kñ: ÷Yñ = ÷jñ, = . После умножения последнего равенства слева на ÷iñ получим: = = = j_i, или = j_i, где = = – матрица оператора , j_i – матрица-строка вектора ÷jñ. Таким образом, оператор представляется матрицей , а векторное уравнение ÷Yñ = ÷jñ – матричным уравнением = j_i.

Уравнение для нахождения собственных значений и собственных векторов оператора ÷Yñ=÷Yñ F в матричном представлении = Y_i F становится линейной однородной системой алгебраических уравнений. Такая система имеет не нулевые решения, если ее детерминант равен нулю. Приравняв его к нулю, получают уравнение, которое дает искомые значения F. Для каждого из найденных значений параметра F решение рассматриваемой системы уравнений (совокупность неизвестных Y_i) и представляет собой матрицу-столбец собственного вектора оператора .

В сопряженном пространстве оператору соответствует оператор ⁺. Он представляется матрицей = . Уравнение ÷Yñ = ÷jñ в матричной форме приобретает вид = j_i⁺. Матрицы оператора в сопряженных пространствах связаны соотношением = , то есть переход в сопряженное пространство осуществляется посредством двух процедур: комплексным сопряжением и транспонированием. Для самосопряженных операторов ⁺ = , поэтому матрицы этих операторов удовлетворяют соотношению = . Их также называют самосопряженными или эрмитовыми.

Алгебра матриц согласована с алгеброй операторов. Так что, например, матрицей произведения операторов является произведение матриц этих операторов. Матрицы коммутирующих операторов тоже коммутируют.

В собственном представлении матрица оператора имеет диагональный вид, причем диагональные элементы совпадают с множеством экспериментально наблюдаемых значений величины, сопоставляемой данному оператору. Приведение матрицы оператора к диагональному виду решает вопрос о спектре величины.

Матричное представление векторов состояний и операторов предполагает, что базисные векторы ÷bñ образуют счетное множество. В часто используемом координатном представлении базисом служат векторы ÷bñ = , образующие несчетное множество.

Координатным представлением вектора состояния является волновая функция = Y(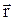), а не матрица-столбец. Суммирование по базисным состояниям заменяется интегрированием по всем 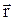. Амплитуду можно представить в виде = Y(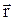). Здесь оператор действует на функцию Y(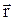), а в выражении – на соответствующий ей вектор ÷Yñ. Одинаковое обозначение не одинаковых операторов не ведет к недоразумениям, поскольку справа от оператора расположен объект, на который направлено его действие. 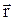Результат применения обоих операторов один и тот же: = = Y() = = j().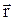

С учетом этих соображений рассуждения, аналогичные случаю счетного множества базисных состояний, приводят к заключению, что уравнение ÷Yñ = ÷jñ в координатном представлении принимает вид Y(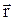) = j(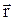), то есть векторы заменяются волновыми функциями. Собственные значения и собственные функции оператора находятся из уравнения Y(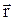) = FY(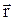). Амплитуда áYïjñ в координатном представлении вычисляется так:

áYïjñ = = = . (10.3)

В некоторых случаях приходится вычислять матричные элементы = , зная волновые функции i-го и k-го состояний:

= = = . (10.4)

В частности, так поступают при нахождении по формуле (9.1) среднего значения величины F в состоянии, описываемом функцией Y():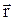

áFñ = = . (10.5)

Запишем в координатном представлении условие самосопряженности оператора (8.4), используя формулу (10.4) для матричных элементов:

ájï úYñ = áYï újñ^*= = . (10.5)

Поменяв местами обкладки под интегралом, оператор следует заменить комплексно сопряженным выражением.

? Контрольные вопросы

1. Как выглядят матрицы состояний микрочастицы в ket-пространстве и в bra- пространстве?

2. Запишите квантово-механическое уравнение ÷Yñ = ÷jñ в матричном виде.

3. Запишите матрицы оператора в исходном и в сопряженном пространствах. Чем отличаются эти матрицы?

4. Какие матрицы являются самосопряженными?

5. Как выглядит матрица оператора в собственном представлении?

6. Запишите в координатном представлении уравнение для нахождения собственных значений и собственных функций оператора .

7. Как находится среднее значение величины F в состоянии Y()?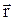

8. Запишите в координатном представлении условие самосопряженности оператора.

F

Задания

10.1. Получите уравнение = j_i⁺.

10.2. Докажите, что матрица оператора в собственном представлении имеет диагональный вид.

10.3. Приведите уравнение ÷Yñ = ÷jñ к виду Y(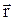) = j().

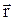10.4. Покажите, что на множестве исчезающих на бесконечности функций операторы x и i d/dx самосопряженные, а оператор d/dx – не самосопряженный.

Дата добавления: 2015-07-11