Наблюдаемые

& Литература: [8], [3], [1], [7].

Наблюдаемыми в квантовой механике называют переменные величины, которые подлежат измерению. Предпринимались попытки построить теорию, в которой использовались не наблюдаемые переменные, «скрытые параметры».

Наблюдаемые в квантовой механике находятся посредством операторов. Постулируется, что каждой наблюдаемой F сопоставляется линейный самосопряженный оператор . Собственные значения этого оператора (действительные, так как оператор самосопряженный) равны тем значениям, которые рассматриваемая величина F может принимать на опыте. Собственные векторы описывают состояния, в которых наблюдаются соответствующие собственные значения.

Если объект находится в состоянии, описываемом собственным вектором úiñ оператора : ÷iñ = úiñ F_i, то при каждом измерении наблюдаемой величины F будет зарегистрировано значение F_i. Таково же будет и ее среднее значение. Система может оказаться в состоянии Y, которое не описывается собственным вектором оператора . Тогда в отдельных измерениях будут регистрироваться те или иные собственные значения F_i оператора , но с различной вероятностью.

Для нахождения этих вероятностей вектор úYñ можно разложить по собственным векторам úiñ оператора , поскольку они образуют полный базис: úYñ = . Коэффициенты этого разложения и дают вероятности i-го собственного значения: W_i = ÷áiïYñç² = áiïYñ* áiïYñ = áYïiñ áiïYñ. Среднее значение величины F находится по формуле

áFñ = = = = 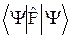. (9.1)

Совместность величин связана с коммутативностью сопоставляемых им операторов. Эта связь устанавливается теоремой о коммутирующих операторах. Необходимым и достаточным условием совместности наблюдаемых величин является коммутативность сопоставляемых им операторов.

Докажем необходимость этого условия. Пусть F и G – совместные величины. Это означат, что в состояниях ÷nñ, в которых F имеет определенные значения F_n, определенные значения G_n имеет и величина G. Тогда

÷nñ = ÷nñ F_n и (9.2)

÷nñ = ÷nñ G_n. (9.3)

Состояние ÷nñ в этом случае можно обозначить и так ÷F_n, G_nñ, подчеркнув тем самым, что вектор ÷nñ является общим для обоих операторов собственным вектором. Применив к обеим частям (9.2) оператор , а к (9.3) – оператор , получим после вычитания: ( – )÷nñ = [ ] ÷nñ = 0. Коммутативность операторов еще не доказана, поскольку нулевым называют оператор, который дает ноль при применении к произвольному вектору. Но общая для обоих операторов система собственных векторов ÷nñ образует полный базис, по которому можно разложить произвольный вектор ÷Yñ. Тогда получим: [ ] ÷Yñ = = 0, так как каждое слагаемое равно нулю.

Докажем, что коммутативность операторов достаточна для совместностисопоставляемых им величин. Ограничимся случаем отсутствия вырождения. Для собственных векторов оператора запишем равенство (9.2). Применим к обеим частям равенства (9.2) оператор и учтем коммутативность операторов: ÷nñ = ( ÷nñ) = ( ÷nñ) F_n. Получается, что вектор ( ÷nñ) есть собственный для оператора , соответствующий собственному значению F_n. Но в (9.2) таковым является вектор ÷nñ. Одно состояние могут описывать разные векторы, если они отличаются постоянным множителем. Так что ÷nñ = ÷nñ G_n, то есть вектор÷nñ является собственным не только для оператора , но и для оператора . Величины, операторы которых имеют общие собственные векторы, совместны. Теорема доказана.

Теорему о коммутирующих операторах можно доказать и с учетом возможного вырождения.

? Контрольные вопросы

1. Что такое наблюдаемые величины?

2. Почему наблюдаемым величинам можно сопоставлять только самосопряженные операторы?

3. Какие значения величины F регистрируются в состоянии, описываемом собственным вектором оператора ?

4. Какие значения величины F регистрируются в произвольном состоянии?

5. Как найти среднее значение величины F в состоянии Y?

6. Чем замечательны операторы совместных величин?

F

Задания

Д. 9.1. Теорема о коммутирующих операторах.

9.1. Докажите, что exp(–x²/2) есть собственная функция оператора –d²/dx² + x², соответствующая собственному значению 1, а x exp(–x²/2) есть собственная функция того же оператора, соответствующая собственному значению 3.

9.2. Найдите собственные функции и собственные значения оператора –d²/dx², действующего на функции, определенные в области 0 £ x £ a и равные нулю на границах этой области. A sin , , 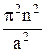n = 1, 2, 3,…

Дата добавления: 2015-07-11