Соотношения неопределенностей для энергии и времени

& Литература: [1], [3].

Из § 15 следует, что если гамильтониан не зависит от времени, то энергия E является интегралом движения. В стационарном состоянии должно сохраняться определенное значение интеграла движения, а для суперпозиции стационарных состояний – его среднее значение. На практике же энергия сохраняется только в состоянии с минимальным ее значением – в основном состоянии. Состояния с большими значениями, так называемые, возбужденные состояния самопроизвольно превращаются в основное состояние. Причина кажущегося расхождения предсказаний теории с практикой заключается в том, что гамильтониан не зависит от времени лишь в нерелятивистском приближении, при котором не существенно квантование электромагнитного поля.

Возбужденным состояниям можно приближенно приписать определенные значения энергии, приблизительно равные собственным значениям оператора Гамильтона. Однако это имеет смысл делать только для промежутков времени, меньших так называемых средних времен жизни t таких состояний.

Возбужденные состояния называют квазистационарными. Квазистационарные состояния характеризуются не только значениями энергии, как это имеет место для стационарных состояний, но и средним временем жизни t.

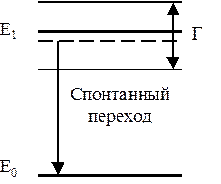Рис. 17.1

На рисунке 17.1 изображена энергетическая диаграмма, соответствующая квазистационарному состоянию. E₀ – наименьшее возможное собственное значение оператора Гамильтона. E₁ – значение, соответствующее рассматриваемому квазистационарному состоянию. G = 2 DE_m – ширина энергетического уровня. DE_m – минимально возможная неопределенность значения энергии, то есть минимально возможное среднеквадратичное отклонение от среднего значения, отмеченного на рисунке 17.1 пунктирной линией.

Величины G и t связаны равенством

G t = ħ. (17.1)

Оно является следствием соотношения неопределенностей для энергии и времени.

Соотношение неопределенностей для энергии и времени можно получить, используя уравнения Гейзенберга (15.2) и соотношения неопределенностей для произвольных несовместных величин F и G:

[ , ] = i Þ DF DG ³ <K> / 2. (17.2)

Пусть 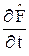= 0. Тогда (15.2) примет вид

= { , } = [ , ]. (17.3)

Положим в (17.2) = и используем равенства (17.3):

[ , ] = –i ħ Þ DE DF ³ 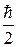< >. (17.4)

Введем промежуток времени Dt такой, чтобы

DF = Dt < >. (17.5)

Тогда неравенство (17.4) примет вид: DE Dt ³ ħ / 2. (17.6)

Это и есть искомое соотношение между неопределенностями энергии и времени. Здесь Dt, в соответствии с (17.5), есть время, в течение которого среднее значение произвольной переменной F изменяется на величину ее неопределенности DF.

В случае квазистационарного состояния интерес представляют минимальная неопределенность энергии DE = DE_min = Γ/2 и минимальное время существенного изменения состояния Dt = Dt_min = t. За время t наиболее быстро изменяющийся параметр F исказит состояние «до неузнаваемости». Таким образом, из соотношения (17.6) для квазистационарного состояния получается равенство (17.1).

Соотношение (17.6) обуславливает существование так называемых виртуальных процессов. Виртуальными именуют процессы, связанные с самопроизвольным увеличением энергии системы на величину, не превышающую неопределенность энергии. Время протекания этих процессов ограничено соотношением неопределенностей для энергии и времени. Виртуальные процессы становятся реальными (увеличение энергии можно измерить), если системе сообщить соответствующее значение энергии.

Виртуальными являются процессы обмена переносчиками взаимодействия. Частицы, которыми обмениваются взаимодействующие объекты, называют виртуальными. Виртуальные частицы становятся реальными, если системе сообщить энергию, превышающую энергию покоя этих частиц.

Соотношение неопределенностей для энергии и времени формально похоже на соотношение неопределенностей Гейзенберга (для проекций импульса и одноименных координат). Однако по смыслу эти соотношения существенно различаются. Дело в том, что соотношение (17.6) относится к изменению состояния, а не к самому состоянию. Величина t не является динамической переменной в отличие, например, от x или p_X.

? Контрольные вопросы

1. Запишите для классической частицы уравнения Гамильтона, используя классические скобки Пуассона.

2. Расскажите о теореме Эренфеста.

3. Расскажите о том, как получается соотношение (16.8).

4. При каких условиях можно применять классическую механику?

5. Что имеют общего и чем отличаются друг от друга уравнения движения в форме Шредингера и в форме Гейзенберга?

6. Какие предсказания о зависимости энергии от времени микрообъекта можно сделать на основе нерелятивистской квантовой механики и как они выполняются на практике?

7. Какое состояние называют квазистационарным? Какими величинами оно характеризуется?

8. Расскажите о связи среднего времени жизни и ширины уровня квазистационарного расстояния.

9. Как получается соотношение неопределенностей для энергии и времени? Какой смысл имеют входящие в него величины?

10. Расскажите о виртуальных процессах.

11. Сравните соотношение неопределенностей Гейзенберга и соотношение (17.6).

F

Задания

18.1. Приведите уравнения (16.1) к виду (16.2).

18.1. Выведите соотношение (16.8).

18.1. Среднее время жизни возбужденного состояния атома 10^–8 с. Найдите ширину энергетического уровня этого состояния. 6,6×10^–7 эВ.

Дата добавления: 2015-07-11