
|
Читайте также: |
& Литература: [1], [2], [7], [8].
 Проанализируем движение частицы в прямоугольной потенциальной яме, изображенной на рисунке 19.1.
Проанализируем движение частицы в прямоугольной потенциальной яме, изображенной на рисунке 19.1.
В каждой из областей I, II, III (рис.19.1) реализуется свободное движение. Так что можно использовать формулы (18.6) и (18.7).
В области I, где U = ¥, для обеспечения конечности Y-функции следует положить A = 0.
Тогда Y1 = B exp (¥ x) = 0. (19.1)
В области II
Y2 = A2 exp (i k2 x) + B2 exp (–i k2 x), (19.2)
где k2 =  . (19.3)
. (19.3)
В области III Y3 = A3 exp(–g x), (19.4)
где g =  . (19.5)
. (19.5)
Из полученных решений для отдельных областей нужно «сшить» единую Y-функцию, удовлетворяющую стандартным условиям и имеющую непрерывную производную везде, кроме точки x = 0.
Условие сшивания в точке x = 0 дает A2 = – B2.
Условия сшивания в точке x = a с учетом последнего равенства принимают вид: A2 2 i sin (k2 a) = A3 exp (–g a), (19.6)
A2 2 i cos (k2 a) = –  A3 exp (–g a). (19.7)
A3 exp (–g a). (19.7)
При отличных от нуля A2 и A3 соотношения (19.6) и (19.7) эквивалентны равенству tg (k2 a) = – k2 / g. (19.8)
Оно имеет место лишь при определенных значениях E. Именно эти значения и составляют энергетический спектр.
Уравнение (19.8) можно решить, например, графическим методом или численно на компьютере. Анализ решения приводит к следующим заключениям:
§ минимально возможное значение энергии (энергия основного состояния) E0 > – U0 в полном соответствии с соотношением неопределенностей Гейзенберга;
§ число возможных значений энергии конечно и растет с ростом параметра U0 a2;
§ при условии  решений не существует, то есть в случае достаточно узкой и мелкой ямы финитное движение невозможно.
решений не существует, то есть в случае достаточно узкой и мелкой ямы финитное движение невозможно.
Для бесконечно глубокой потенциальной ямы (U0 ® – ¥) соотношение (19.8) дает: E + U0» En =  (n + 1)2, (19.9)
(n + 1)2, (19.9)
где n –– квантовое число (n = 0, 1, 2,…).
Волновая функция в этом случае при 0 £ a £x имеет вид:
Y =  . (19.10)
. (19.10)
Вне указанной области она равна нулю.
Движение микрочастицы в потенциальной яме качественно отличается от движения классической частицы:
§ энергетический спектр микрочастицы дискретен;
§ уровень минимально возможной энергии выше дна потенциальной ямы;
§ микрочастицу можно обнаружить вне ямы вблизи ее края, если яма здесь имеет конечную глубину;
§ внутри ямы есть точки (узлы волновой функции), недоступные для микрочастицы.
При n ® ¥ различия в поведении микрочастиц и классических частиц исчезают. В этом проявляется принцип соответствия.
? Контрольные вопросы
1. Какие конкретные системы моделирует задача о прямоугольной потенциальной яме?
2. Какие значения принимает потенциальная функция в различных областях ямы, и какой вид для них имеет волновая функция?
3. Какие свойства волновой функции используются при нахождении энергетического спектра микрочастицы в прямоугольной потенциальной яме?
4. Расскажите об энергетическом спектре микрочастицы в прямоугольной потенциальной яме. Почему энергетический спектр электронов в металле называют квазинепрерывным, и почему его дискретность оказывается существенной?
5. Сравните поведение микрообъекта и классической частицы в потенциальной яме.
|
19.1. Для потенциальной ямы, изображенной на рисунке 19.2, нарисуйте графики волновых функций микрочастиц, обладающих энергиями E1 и E2.
19.2. 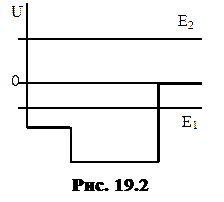 Решите уравнение Шредингера для микрочастицы, находящейся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками и найдите энергетический спектр.
Решите уравнение Шредингера для микрочастицы, находящейся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками и найдите энергетический спектр.
| 0, если 0 £ x £ a, 0 £ y £ b, 0 £ z £ c. ¥, если x < 0, x > a, y < 0, y > b, z <0, z > c. |
19.3. 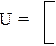 Найдите волновую функцию и энергетический спектр частицы, находящейся в потенциальном поле, определяемом следующим образом:
Найдите волновую функцию и энергетический спектр частицы, находящейся в потенциальном поле, определяемом следующим образом:
19.4.
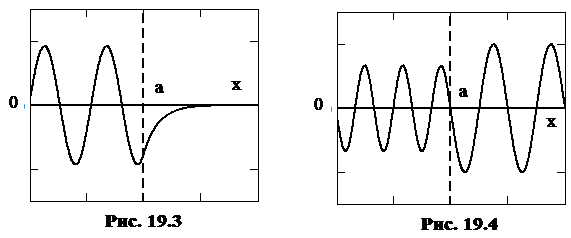 |
Дата добавления: 2015-07-11; просмотров: 125 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свободное движение микрочастиц | | | Прохождение частицы через потенциальный барьер. Туннельный эффект |