Прохождение частицы через потенциальный барьер. Туннельный эффект

& Литература: [1], [2], [7], [8].

Прохождением через потенциальный барьер называют движение частицы в области пространства, где потенциальная функция имеет максимум. В качестве примеров подобных движений можно назвать: перекатывание шарика через горку, вырывание электрона из металла электрическим полем (холодная эмиссия), вылет a-частицы из тяжелого ядра (a-распад) и другие.

Укажем основные идеи и этапы решения задачи о прямоугольном потенциальном барьере, изображенном на рисунке 20.1.

Барьер имеет ширину a и высоту U₀. Энергия частицы – E.

Для каждой из указанных на рисунке областей I, II, и III решение уравнения Шредингера имеет вид волновой функции свободного движения:

Y_j = A_j exp (i k_j x) + B_j exp–i k_j x), (20.1)

где j = 1, 2, 3; k₁ = k₃ = , (20.2)

k₂ = . (20.3)

Цель расчетов – найти коэффициент отражения барьера

R = |B₁|² / |A₁|², (20.4)

а также коэффициент прозрачности D = 1 – R. (20.5)

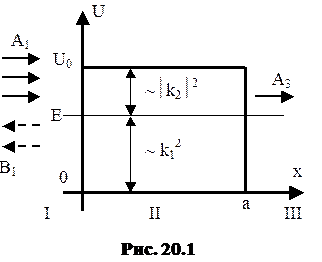Эти коэффициенты представляют собой вероятности того, что частица, соответственно, отразится от барьера или что она преодолеет его.

Произвольные постоянные A_j и B_j должны обеспечивать для волновой функции выполнение стандартных условий, а также непрерывность производной. Соответствующие условия на границах x = 0 и x = a называют условиями сшивания.

Положим для определенности, что частицы попадают на барьер только слева (рис.20.1). Тогда B₃ = 0. Условия сшивания в точке x = 0 принимают вид:

A₁ + B₁ = A₂ + B₂, (20.6)

k₁ A₁ – k₁B₁ =k₂ A₂ – k₂B₂, (20.7)

а в точке x = a:

A₂ exp (i k₂ a) + B₂ exp (–i k₂ a) = A₃ exp (i k₁ a), (20.8)

k₂ A₂ exp (i k₂ a) – k₂ B₂ exp (–i k₂ a) =k₁ A₃ exp (i k₁ a). (20.9)

Исключая из системы (20.8) и (20.9) вначале A₂, а затем B₂, получим

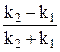= exp (2 i k₂ a). (20.10)

Проделав аналогичные процедуры с (20.6) и (20.7), найдем

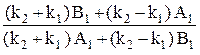= . (20.11)

Приравнивая (20.10) и (20.11), вычислим отношение

R = = . (20.12)

Заметим, что формула (20.12) справедлива как для случая E < U₀ (высокий барьер), так и для случая E > U₀ (низкий барьер).

Из (20.12) следует, что

D = 1 – R = . (20.13)

На практике пользуются приближенной формулой для коэффициента прозрачности, которая получается из (20.13), если положить k₁ = k, k₂ = i k,
a k >> 1: D ≈ exp (– 2 a k) = exp . (20.14)

В отличие от классической частицы микрообъект может преодолеть даже высокий (E < U₀) потенциальный барьер с вероятностью, определяемой формулой (20.13) (или (20.14)). Энергия E при этом остается постоянной, то есть работа над частицей не совершается. Преодоление микрочастицей высокого потенциального барьера без совершения работы называют туннельным эффектом.

Преодоление потенциального барьера произвольной формы можно рассматривать как последовательное прохождение множества узких почти прямоугольных барьеров шириной dx и высотой U(x) – E (рис. 20.2). Перемножив вероятности прохождения этих барьеров, найденные по формуле (20.14), получим выражение для искомого коэффициента прозрачности:

D ≈ exp . (20.15)

Пределы интегрирования x₁ и x₂ (рис.20.2) являются корнями уравнения

U(x) – E = 0.

? Контрольные вопросы

1. Расскажите о потенциальных барьерах для классических частиц и для микрообъектов. Какие величины характеризуют преодоление барьеров?

2. Расскажите о туннельном эффекте.

3. Какой вид имеет волновая функция в различных областях прямоугольного потенциального барьера?

4. Какие условия сшивания используются при решении задачи о прямоугольном потенциальном барьере?

5. Сравните преодоление потенциального барьера классической частицей и микрообъектом.

6. Как подсчитать коэффициент прозрачности для барьера произвольной формы?

7. Приведите примеры проявления туннельного эффекта? Имеет ли он место для макроскопических тел?

F

Задания

21.3 Получите выражения (20.12) и (20.13) для коэффициента отражения и для коэффициента прозрачности прямоугольного потенциального барьера.

21.4 Получите из (12.13) приближенную формулу (12.14).

21.5 Электрон проходит через потенциальный барьер, создаваемый полем E. Максимальное значение потенциальной энергии превышает энергию электрона на величину U₀. Определите коэффициент прозрачности барьера D. D = exp .

Дата добавления: 2015-07-11