Ротатор. Собственные функции и собственные значения операторов орбитального момента импульса

& Литература: [1], [3], [8], [7].

Центральным полем называют поле, потенциальная функция которого зависит только от расстояния до некоторого центра. При движении в таком поле сохраняется момент импульса частицы. Это справедливо как для корпускулы, так и для микрочастицы. Простейшим примером движения в центральном поле является движение гантели вокруг цента масс, которое сводится к движению одной m-точки вокруг этого центра. Рассмотрим квантовомеханический аналог такого движения.

Ротатором называют систему, описываемую гамильтонианом

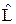= ² / (2 I), (22.1)

где 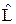² – оператор квадрата момента импульса, а I – момент инерции. Примером ротатора является двухатомная молекула, если расстояние между ее атомами можно считать неизменным.

Стационарное уравнение Шредингера для ротатора Y = E Y сводится к уравнению 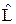² Y = L² Y, (22.2)

которое определяет собственные значения L² и собственные функции Y оператора квадрата момента импульса 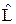². Значение задачи о моменте импульса далеко выходит за рамки проблемы собственно ротатора.

Задача решается в сферической системе координат. Оператор квадрата момента импульса в этой системе имеет вид:

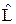² = – ħ ² 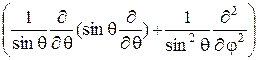. (22.3)

Он зависит только от сферических координат q и j. Подстановка (22.3) превращает (22.2) в известное в математике уравнение для сферических функций. Этим уравнением занимался еще А. М. Лежандр задолго до создания квантовой механики.

Уравнение для сферических функций имеет непрерывное и конечное решение только при условии: L² = ħ ² l (l + 1). (22.4)

В этом случае сферические функции выражаются через присоединенные полиномы Лежандра P _l ^½m½(cos q), аргументом которых является cos q:

Y _{l m} (q, j) = N _{l m} P _l ^½m½(cos q) exp (i m j). (22.5)

Коэффициенты N _{l m} – нормирующие множители, а числа m для обеспечения однозначности волновой функции вида (22.5) могут принимать лишь следующие значения: m = l, l– 1, ¼ – l.

Так получаются собственные функции (22.5) и собственные значения (22.4) оператора 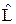² . l – орбитальное квантовое число. Смысл квантового числа m выясняется при подстановке (22.5) в уравнение для собственных значений оператора проекции момента импульса 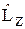= – i ħ :

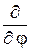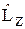Y _{l m} = L_Z Y _{l m}. (22.6)

Это равенство становится тождеством при L_Z = ħ m. (22.7)

Таким образом, квантовое число m является квантовым числом проекции момента импульса (магнитным квантовым числом).

Из (22.5) следует, что величина |Y _{l m}|² = r(q) не зависит от j, то есть пространственное распределение плотности вероятности симметрично относительно оси z, от которой отсчитывается координатный угол q. По этой причине пространственное распределение плотности вероятности изображается с помощью полярных диаграмм r(q).

Квантование квадрата момента импульса (22.4) определяет энергетический спектр ротатора: E = 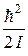l (l + 1). (22.8)

Формула (22.8) согласуется с наблюдаемыми на опыте ротационными спектрами молекул.

? Контрольные вопросы

1. Для каких систем применима модель ротатора?

2. Какое отношение к ротатору имеет задача о нахождении собственных функций и собственных значений операторов момента импульса?

3. Расскажите о том, как находятся собственные значения операторов момента импульса?

4. Расскажите о полярных диаграммах, отражающих собственные функции операторов момента импульса.

5. Расскажите об энергетическом спектре ротатора.

F

Задания

25.1. Получите соотношение (22.7).

25.2. Нарисуйте полярные диаграммы для p-состояний. Опишите такие распределения частиц, находящихся на поверхности шара, которые соответствуют этим диаграммам.

25.3. Докажите, что ротационные спектры молекул удовлетворяют соотношению: w = (ħ / I) l. Учтите, что орбитальное квантовое число l при излучении должно изменяться только на единицу.

Дата добавления: 2015-07-11