
Читайте также:
|
& Литература: [1], [8].
Задача о системе двух частиц относится, например, к атому водорода, мезоатому, позитронию. Как и в классической механике, она сводится к задаче об одной частице.
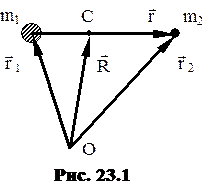 На рисунке 23.1 изображены две частицы. Их массы m1 и m2, а радиус-векторы
На рисунке 23.1 изображены две частицы. Их массы m1 и m2, а радиус-векторы  1 и
1 и  2. Величина
2. Величина  =
=  2 –
2 –  1 (23.1)
1 (23.1)
определяет положение второй частицы относительно первой. С – центр масс системы. Его радиус-вектор 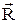 =
= 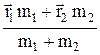 . (23.2)
. (23.2)
Гамильтониан рассматриваемой системы
 =
= 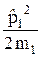 +
+ 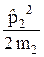 + U(r)
+ U(r)
посредством замены переменных (23.1) и (23.2) можно представить в виде суммы независимых частей:
 =
=  (
(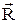 ) +
) +  (
( ). (23.3)
). (23.3)
Отсюда следует, что волновая функция Y( 1,
1,  2) системы равна произведению собственных функций этих частей:
2) системы равна произведению собственных функций этих частей:
Y( 1,
1,  2) = Y(
2) = Y(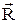 ) Y(
) Y( ). (23.4)
). (23.4)
Собственная функция Y(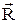 ) гамильтониана
) гамильтониана  (
(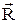 ) описывает движение частицы массой (m1 + m2), которая находится в центре масс С.
) описывает движение частицы массой (m1 + m2), которая находится в центре масс С.
Второе слагаемое в формуле (23.3) имеет вид
 (
( ) =
) = 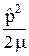 + U(
+ U(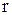 ), (23.5)
), (23.5)
где m = m1 m2 / (m1 + m2). (23.6)
Собственная функция Y( ) этого гамильтониана характеризует движение m-точки, то есть частицы массой m (10.6) и радиус-вектором
) этого гамильтониана характеризует движение m-точки, то есть частицы массой m (10.6) и радиус-вектором  (10.1), относительно центра масс С; m-точка находится в поле, потенциальная функция U(
(10.1), относительно центра масс С; m-точка находится в поле, потенциальная функция U( ) которого описывает взаимодействие рассматриваемых частиц.
) которого описывает взаимодействие рассматриваемых частиц.
Таким образом, задача сводится к решению стационарного уравнения Шредингера для m-точки, находящейся в центральном поле:
 (
( ) Y(
) Y( ) = E Y(
) = E Y( ). (23.7)
). (23.7)
Центральная симметрия обуславливает использование сферических координат r, q, j. В этих координатах гамильтониан (23.5) можно представить следующим образом:
 (
( ) = –
) = – 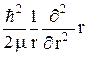 +
+ 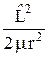 + U(r), (23.8)
+ U(r), (23.8)
где 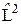 выражается формулой (22.3), то есть является оператором квадрата момента импульса.
выражается формулой (22.3), то есть является оператором квадрата момента импульса.
Благодаря (23.8) решение уравнения (23.7) можно искать в виде
Y( ) = R(r) Y l m (q, j), (23.9)
) = R(r) Y l m (q, j), (23.9)
где угловая часть волновой функции Y l m (q, j) является собственной функцией оператора 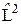 . Она определяется соотношением (22.5) и соответствует собственным значениям (22.4).
. Она определяется соотношением (22.5) и соответствует собственным значениям (22.4).
Учтя (22.4) при подстановке (23.9) и (23.8) в (23.7), получим уравнение для радиальной части R(r)волновой функции:
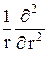 r R(r) +
r R(r) + 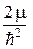 (E – U (r) –
(E – U (r) – 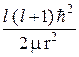 ) R(r) = 0. (23.10)
) R(r) = 0. (23.10)
Уравнение (23.10) определяет также и энергетический спектр. Видно, что энергия E не может зависеть от магнитного квантового числа m, но может зависеть от числа l.
? Контрольные вопросы
1. Как осуществляется разделение переменных при решении задачи о системе двух частиц? К каким более простым задачам она сводится?
2. Что такое m-точка? Какой она имеет смысл для атома водорода?
3. Что такое угловая и что такое радиальная части волновой функции? Какой смысл имеют содержащиеся в них квантовые числа?
4. Какую информацию об энергетическом спектре содержит в себе уравнение Шредингера для радиальной части волновой функции?
|
23.1. Получите соотношение (23.3).
23.2. Получите выражение (23.8), используя формулу для оператора Ñ2 в сферической системе координат:
Ñ2= 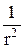
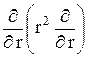 +
+ 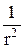
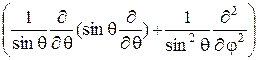 (23.11)
(23.11)
23.3. Получите уравнение (23.10).
Дата добавления: 2015-07-11; просмотров: 103 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ротатор. Собственные функции и собственные значения операторов орбитального момента импульса | | | Решение квантово-механической задачи об атоме водорода |