Решение квантово-механической задачи об атоме водорода

& Литература: [1], [3], [8], [7].

Соотношения (23.9) и (23.10) справедливы для любых центрально симметричных полей. В атоме водорода поле – центрально симметричное, и оно описывается потенциальной функцией

U(r) = – k e² / r, где k = 1 / (4 p e₀). (24.1)

Целесообразно перейти к безразмерным переменным

r = r / r₀ и e = – E / E_R, (24.2)

где r₀ = ħ ² / (m e² k) – боровский радиус, а (24.3)

E_R = k² m e⁴ / (2 ħ ²) – энергия Ридберга. (24.4)

Уравнение Шредингера для радиальной части R(r) волновой функции в безразмерных переменных принимает вид

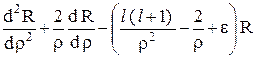= 0. (24.5)

Решение уравнения (24.5) ищется в виде

R = f exp (– r 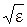), (24.6)

так как второй сомножитель в (24.6) удовлетворяет уравнению (24.5) при r®¥. Подставляя (24.6) в (24.5), получим уравнение, которому должна удовлетворять функция f(r):

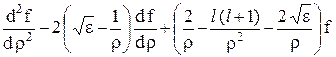= 0. (24.7)

Функцию f = f(r) представляют в виде степенного ряда

f = r ^l 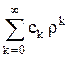= 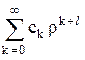. (24.8)

Нулевой член ряда (24.8) дает асимптотическое решение (24.7) при r ® 0. Коэффициенты c_k должны обеспечить обращение равенства (24.7) в тождество. Тождество будет иметь место при выполнении следующего рекуррентного соотношения:

c_k+1 = c_k 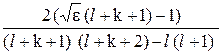. (24.9)

Сравнение степенного разложения функции r ^l exp (2 r 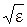) с рядом (24.8) приводит к заключению, что при r ® ¥ функция f ® r ^l exp (2 r 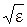) и, следовательно, R(r) ® ¥, чего не может быть для волновой функции. Конечность волновой функции будет обеспечена, если числитель в формуле (24.9) при k = n_r обратится в нуль. Тогда ряд (24.8) станет полиномом степени l + n_r, и функция (24.6) при r ® ¥ будет стремится к нулю. Этого можно достичь, подобрав параметр e так, чтобы 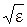(l + n_r +1) – 1 = 0, или

E = – E_R / n², (24.10)

где n = l + n_r + 1 – (24.11)

главное квантовое число, а величину n_r, определяющую степень полинома f (24.8), называют радиальным квантовым числом.

Искомая радиальная часть волновой функции (24.6) принимает вид:

R = r ^l L_{n l} (2 r / n) exp (– r 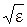), (24.12)

где L_{n l} (x) – известные в математике полиномы Лагера аргумента x = 2 r / n. Приведем для примера несколько таких полиномов:

L₁₀ (x) = L₂₁ (x) = 1; L₂₀ (x) = 2 – x; L₃₁ (x) = 6 – x; L₃₀ (x) = 21 –18 x + 2 x².

? Контрольные вопросы

1. Перечислите основные положения, используемые при решении задачи об атоме водорода.

2. Какова угловая часть волновой функции атома водорода?

3. В каком виде и почему разыскивается решение уравнения Шредингера для радиальной части волновой функции атома водорода?

4. Почему ряд, посредством которого выражается решение уравнение Шредингера, превращают в полином?

5. Расскажите о радиальном и главном квантовых числах. Какие значения может принимать число l при фиксированной величине n?

F

Задания

25.4. Приведите уравнение (23.10) к виду (24.5).

25.5. Получите уравнение (24.7).

25.6. Проверьте подстановкой, что формулы (24.6) и (24.8) при
r ® 0 удовлетворяют уравнению (24.5).

25.7. Получите рекуррентное соотношение (24.9).

25.8. Докажите, что при r ® ¥ ряд 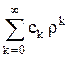® exp (2 r 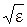), если коэффициенты c_k удовлетворяют соотношению (24.9).

Дата добавления: 2015-07-11