А — движение в первой фазе наезда; б — движение во второй фазе наечда

Рис. 7.6 Экспериментальный график <время — перемещение» при наезде автомобиля на неподвижное препятствие

ИЛИ

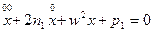(7.4)

где ; ;

Линейное дифференциальное уравнение второго по­рядка имеет решение:

где 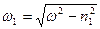а и —постоянные интегрирования, определяемые из начальных условий.

Скорость автомобиля в первой фазе находим, про­дифференцировав формулу (7.5) по времени:

(7.6)

Пользуясь выражениями (7.5) и (7.6), можно найти перемещение и скорость автомобиля в любой момент времени t, если известны начальные условия движения и характеристики системы.

Можно также решить и обратную задачу: опреде­лить неизвестные характеристики по известным парамет­рам движения автомобиля при наезде его на неподвиж­ное препятствие.

Во время полигонных испытаний на удар автомобиль наезжает с заданной начальной скоростью на жесткое неподвижное препятствие (по Правилам ЕЭК ООН — железобетонный куб массой не менее 20 т).

Процесс удара фиксируют с помощью скоростной киносъемки, а также чувствительных датчиков, установ­ленных в различных местах автомобиля. Расшифровав кинограмму, строят график (рис. 7.6, а).

Начальный момент времени (t = 0) совпадает с нача­лом контакта автомобиля с препятствием. Тангенс угла наклона касательной к кривой на ее начальном участке характеризует скорость 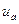автомобиля перед ударом. Точка А перегиба кривой означает конец первой фазы — остановку автомобиля. Координаты этой точки соответ­ствуют времени движения автомобиля от начала кон­такта с препятствием до остановки и максимальную деформацию передней части .

Для определения пяти неизвестных, входящих в урав­нения (7.5) и (7.6), т. е. , , , , , напишем дополнительные соотношения. В начальный момент кон­такта автомобиля с препятствием, т. е. при t = 0,

x (0) = 0; х (0) = 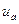. (7.7)

В момент остановки автомобиля, т. е. при t = ,

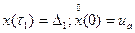(7.8)

Пятое недостающее условие найдем, выбрав на экспе­риментальном графике какую-нибудь точку и определив ее координаты. Например, в момент времени /2 пере­мещение равно x( /2)= (точка О). Подстановка ука­занных значений х и х в формулы (7.5) и (7.6) дает систе­му из пяти трансцендентных уравнений, которые могут быть решены с помощью ЭЦВМ. Более простое решение можно получить, несколько упростив расчетную схему, например, предположив, что сила сухого трения отсут­ствует ( =0). Тогда, используя формулу (7.7), нахо­дим постоянные интегрирования: = 0 и = . После этого, применив формулы (7.8), получаем:

(7.9)

(7.10)

Определив из формулы (7.9) значение , подставим его в формулу (7.10). Обозначив для краткости , придем к уравнению:

(7.11)

Это уравнение содержит лишь одно неизвестное — . Остальные параметры находят по экспериментальному графику «время—перемещение» (см. рис. 7.6). Решая равенство (7.11), находим , а затем и остальные харак­теристики системы.

Во время второй фазы наезда (см. рис. 7.5, б) детали передней части, сжатые в первой фазе, распрямляются и автомобиль удаляется от препятствия. Сила 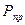стано­вится движущей, а силы 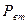и меняют знак на обратный. Для обозначения характеристик системы (К, ) сохраним те же буквенные обозначения, но, учитывая изменение физических свойств детали в результате удара, заменим индекс 1 на 2. Начало координат выбираем в положе­нии, где находится центр тяжести в момент начала дви­жения автомобиля в обратном направлении. Положитель­ное направление оси х — в сторону движения автомобиля.

На графике «время—перемещение» (см. рис. 7.6) вто­рая фаза представлена участком кривой АВ.

Точка В соответствует моменту отрыва автомобиля от препятствия, а касательная к кривой в этой точке харак­теризует мгновенную скорость автомобиля в конце второй фазы наезда. Разность абсцисс этих точек (А и В) дает время второй фазы, а разность ординат — упругую деформацию 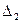. Ордината точки В (разность — 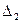) характеризует остаточную деформацию Лз передней части автомобиля. Составив уравнение движения системы и решив его, можно получить формулы для определения перемещения и скорости автомобиля во второй фазе при известных значениях , , .

Так, например, при = 0:

(7.12)

Можно также, использовав данные эксперимента, найти коэффициенты и , а также силу для фазы отката.

В табл. 7.1 и 7.2 приведены средние значения характе­ристик в обеих фазах удара для некоторых автомобилей (получены О. Г. Кузнецовым путем обработки результа­тов испытаний, проведенных ЦНИИАП НАМИ). Для отечественных легковых автомобилей в первой фазе удара сила близка к нулю, и процесс удара в этой фазе

Таблица 7.1. Характеристики наезда на неподвижное препятствие отечественных автомобилей

Автомобили	Первая фаза	Вторая фаза
		.С			, С
ВАЗ-2101; -2103; -2106; -2105; -2107 ВАЗ-2108; 2109; -2110	575 000	8900 12400	0,080	929 000 1 050 000	31600 26800	0,083
ВАЗ-2121 ИЖ-1500; Москвич-412	800 000 464 000	4200 14400	0,063	1 143000 622 000	22700 9500	0,090
ГАЗ-24; -3102	524 000	22 200	0,073	1 042 070	11 800	0,0785
ЗАЗ-966;-968;-1102			0,077	1 066 945	21,300	0,045

Таблица 7.2. Ударные характеристики автомобилей при наезде на неподвижное препятствие

Автомобили	Начальная скорость, м/с	Коэффициент упругости	Коэффициент восстановле­ния	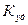Замедление при откате J, м/с2	Число испы­тан­ных авто­моби­лей
ВАЗ-21212 ВАЗ-2121 ВАЗ-21055 ВАЗ-21013 ВАЗ-2101 ВАЗ-2107 ВАЗ-2108 ВАЗ-21093 ВАЗ-21086 ВАЗ-2110 ВАЗ-2103 ГАЗ-3102 ГАЗ-24 ИЖ-1500 Москвич-412 ЗАЗ-968 ЗАЗ-1102 Фиат-126 Воксхолл КаВЗ-685	14,9 14,0—14,3 13,9 13,9 14,0—14,2 14,0 14,1 13,3 13,9 14,0 14,1—14,3 13,9 13,5 13,9—14,4 13,9 13,9—14,3 13,8—14,4 13,4 11,8 11,8	1,21—1,24 1,16—1,32 1,20 1,29 1,25—1,32 1,15 1,34—1,29 1,22 1,23 1,13—1,15 1,19—1,21 1,26—1,32 1,30 1,17-1,37 1,45—1,60 1,17—1,22 1,1 —1,31 1,32 1,22 1,05	0,117—0,132 0,086—0,132 0,090 0,101 0,086—0,102 0,099 0,099—0,106 0,120 0,113 0,104—0,130 0,090—0,092 0,129 0,134 0,090—0,115 0,110—0,136 0,102—0,146 0,110—0,143 0,164 0,118 0,170	5,10—6,50 2,90—6,32 2,44 3,50 5,10—8,50 4,76 3,80—6,25 5,12 4,76 4,26 4,97-7,04 5,16 5,30 4,50—6,40 5,23—5,84 2,50—5,70 1,60—7,30 2,00 4,90 10,50

хорошо описывается уравнением (7.11). Во второй фазе сила отрицательна. Это может быть результатом нелинейности коэффициента , характеризующего упру­гость деталей, деформированных во время первого этапа удара.

На рис. 7.6, б кривая I построена по результатам экс­перимента, а кривые 2 и З получены расчетом. Для кривой 2 принято <. О, а для кривой 3— = 0.

С помощью таблиц можно по формуле (7.12) найти скорость автомобиля в момент отделения его от препят­ствия, а затем, используя понятие коэффициента удара, определить начальную скорость автомобиля.

Найти начальную скорость автомобиля можно также, если на месте ДТП замерено расстояние между авто­мобилем и препятствием после отката. На эксперимен­тальном графике (см. рис. 7.5) точка С соответствует остановке автомобиля после его отката от препятствия. Разность абсцисс точек С и В определяет продолжитель­ность третьей фазы , а разность их ординат — пере­мещение автомобиля в процессе отката. Сумма дает общую продолжительность наезда Тн. Учитывая кратковременность процесса отката (продолжа­ющегося менее I с), можно приближенно считать все силы, действующие при этом на автомобиль, постоянными, и движение его — равнозамедленным.

Тогда перемещение автомобиля в третьей фазе

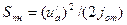
где — замедление автомобиля при откатывании от препят­ствия, м/с².

Замедление зависит от степени разрушения автомобиля при ударе. Если поломки сравнительно невелики и с по­верхностью дороги контактируют только шины автомо­биля, то можно считать, что замедление автомобиля на­ходится в пределах . При этом, как показывают полигонные испы­тания (см. табл. 7.2), значение ближе к верхнему пределу, определяемому силой сцепления шин с дорогой. На сухом асфальтобетоне в среднем = 4,5—5,5 м/с².

Если же скорость автомобиля перед ударом была большой и поломки деталей велики, то возможны меха­ническое зацепление деформированных частей с покры­тием дороги и образование на нем глубоких царапин

и выбоин. В этом случае, как показывают наблюдения, замедление может быть значительным и в некоторых случаях превышает g. Этот вопрос требует дальнейшего изучения.

Таким образом скорость автомобиля перед наездом можно определить двумя путями: по известной остаточ­ной деформации и по известному пути отката . Остаточную деформацию находят, замерив длину автомо­биля после его наезда на препятствие.

Примерная последовательность расчета по деформа­ции такова.

1. Остаточная деформация передней части автомобиля .

2. Полная деформация передней части

3. Упругая деформация передней части

4. Скорость автомобиля в момент его отделения от препятствия - формула (7.12).

5. Начальная скорость автомобиля, если водитель перед наездом не тормозил,

(7.13)

Если водитель применил торможение и на покрытии оставлены следы длиной 5ю, то

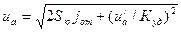(7.14)

При известной длине пути отката расчеты более просты.

1. Скорость автомобиля в момент его отделения от препятствия

2. Начальная скорость автомобиля при наезде без тор­можения—формула (7.13);

при наезде с торможением—формула (7.14). Экспериментальные данные, приведенные в табл. 7.1 и 7.2, действительны для фронтального наезда автомобиля на препятствие с плоской вертикальной поверхностью. При таких наездах все детали, расположенные в одной вертикальной плоскости, контактируют с препятствием одновременно и деформируются на один и тот же раз­мер. При наезде автомобиля на сосредоточенное препят­ствие (столб, дерево) с ним контактируют только неко­торые детали, и повреждения приобретают другой харак­тер. Жесткость и прочность автомобиля по ширине

различны: по сторонам его расположены лонжероны рамы или другие несущие детали кузова, хорошо выдер­живающие перегрузки, в средней же части находятся обычно легко деформируемые детали. Поэтому, напри­мер, удар с одной и той же скоростью о железобетон­ную мачту передним углом автомобиля или его серединой имеет различные последствия.

Чтобы количественно оценить результаты повреждений при наездах различного вида, иногда определяют объем деформированной части автомобиля. Вычислив энергию, необходимую для такого разрушения, ее сравнивают с энергией, определенной при наезде автомобиля на плос­кую поверхность в условиях полигонных испытаний. К сожалению в этом направлении сделаны только первые шаги и опубликованы лишь разрозненные сведения о по­вреждениях автомобилей.

Отсутствуют также данные о снижении ударных свойств автомобиля в процессе его эксплуатации. Данные табл. 7.1 и 7.2 относятся к новым автомобилям и неиз­вестно, как они могут быть применены к автомобилям, срок эксплуатации которых заканчивается. Встречаю­щиеся в литературе предложения по проведению массовых экспериментов для накопления информации о действи­тельных ударных характеристиках автомобилей, находя­щихся в эксплуатации, нельзя считать достаточно обосно­ванными.

После фронтального удара перемещение автомобиля обычно невелико. В случае внецентренного удара оно, напротив, может быть значительным. При внецентренном ударе автомобиль поворачивается в горизонтальной плос­кости на некоторый угол ац. Центр его тяжести переме­щается по дуге радиусом рц (рис. 7.7), а шины скользят по покрытию в поперечном направлении. Считая, что вся кинетическая энергия после удара перешла в работу трения шин по дороге, находим минимальное значение скорости автомобиля перед ударом

ти1/2 == 0<р,,5ц == С(р„ацрц,

Рис. 7 7. Внецентренный удар ав­томобиля на неподвижное пре­пятствие

Рис. 7.8. Зависимости деформа­ции кузова и силы удара от скорости автомобиля

где 5ц — перемещение центра тяжести, замеренное по дуге;

ац — угол поворота автомобиля при ударе; рц — расстояние от препятствия до центра тяжести автомобиля.

Следовательно, иа==л/2^(р1/ацрц-

Иногда используют экспериментально установленные зависимости между скоростью автомобиля и деформацией. В качестве примера на рис. 7.8 показаны зависимости между скоростью автомобиля «Польский Фиат 125 В», деформацией Л (сплошные линии) и силой удара Руд (штриховые линии). Крестиками на рисунке отмечены данные, полученные при наезде на жесткое препятствие, а точками — на аналогичный стоящий автомобиль. Как видно на рисунке, зависимости Руд=/(иа) и Л=г|5(иа) хорошо аппроксимируются прямыми линиями. При наезде на неподвижное препятствие ударная нагрузка больше, а деформация меньше, чем при наезде на автомобиль.

При наличии подобных графиков скорость автомобиля может быть установлена с нужной точностью. К сожа­лению, число достоверных данных весьма ограничено.

При осмотре места ДТП должно быть установлено расстояние видимости препятствия. Если это не сделано, то нужно провести следственный эксперимент и определить это расстояние при сходных условиях (погодных, времен­ных и т. д.). После этого, зная начальную скорость авто­мобиля, вычисляют длину остановочного пути. Сравнивая ее с расстоянием видимости, определяют техническую возможность предотвращения наезда путем экстренного торможения или маневра.

Дата добавления: 2015-10-16