Критические скорости автомобиля

Технической причиной ДТП может быть плохая устой­чивость автомобиля. Управляя неустойчивым автомо­билем, водитель вынужден сосредоточивать внимание на нем, постоянно корректируя его движение и отвлекаясь от наблюдения за окружающей обстановкой. Длитель­ная работа на неустойчивом транспортном средстве приводит к нервному перенапряжению водителя и быст­рому его утомлению, повышает вероятность ошибок при управлении автомобилем.

Нарушения устойчивости автомобиля проявляются в произвольном изменении направления движения (рысканье), скольжении шин по дороге и опрокидывании. Выезд автомобиля в соседний ряд, на встречную сторону проезжей части или за пределы дороги — наиболее частые последствия недостаточной устойчивости. Анали­зируя ДТП с подобными обстоятельствами, эксперты обычно определяют критическую скорость автомобиля, т. е. максимально возможную скорость, при которой еще сохраняется устойчивое движение транспортного средства.

Потеря устойчивости наиболее вероятна на участках дороги со скользким неровным покрытием (укатанный снег, обледенелый асфальтобетон или булыжник) и кру­тыми подъемами. Если тяговая сила станет примерно равной силе сцепления, то даже небольшая поперечная сила может вызвать боковое скольжение ведущих колес по дороге. Такие возмущающие силы могут возникнуть от ударов о неровности дороги, порывов бокового ветра и других причин. Пробуксовка колес переднего моста не переходит в прогрессирующий занос и не представ­ляет опасности. Гораздо опаснее буксование колес задне­го моста.

При прямолинейном движении автомобиля показа­телем устойчивости является критическая скорость по условиям буксования ведущих колес . Так, при движении по горизонтальной дороге автомобиля с задним ведущим мостом

(6.1)

для автомобиля с передним ведущим мостом

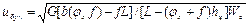(6.2)

Буксование ведущих колес не всегда приводит к за­носу, тем более к ДТП. Водитель, заметив пробуксовку, обычно имеет возможность уменьшить тяговую силу. В большинстве случаев начавшееся буксование стано­вится опасным лишь в сочетании с неправильными или несвоевременными действиями водителя транспорт­ного средства.

Прямолинейное движение автомобиля практически наблюдается довольно редко. Даже на прямолинейных участках дороги водитель все время поворачивает руле­вое колесо, выравнивая автомобиль, отклоняющийся под действием случайных возмущений. В опасных и кри­тических дорожных ситуациях, предшествующих куль­минационной фазе ДТП, криволинейное движение авто­мобиля часто связано с потерей поперечной устойчи­вости под действием центробежной силы.

В теории автомобиля известны формулы для опре­деления скорости Уск, максимально допустимой («кри­тической») по условиям поперечного скольжения и опро­кидывания. Если автомобиль движется накатом, то можно считать, что продольные силы в контактах шин с дорогой отсутствуют и все сцепление используется только в поперечном направлении. Тогда критическая скорость автомобиля по условиям поперечного скольже­ния шин по дороге

(6.3)

где R — расстояние от центра поворота до середины заднего моста автомобиля; — коэффициент поперечного сцеп­ления шин с дорогой; - угол поперечного уклона дороги.

На дороге с двухскатным профилем верхние знаки в формуле (6.3) соответствуют правому повороту, а ниж­ние — левому. На дороге без поперечного уклона ( = 0):

(6.4)

Коэффициент зависит от тех же факторов, что и . Численные значения для большинства шин и дорож­ных покрытий неизвестны. Имеющиеся эксперименталь­ные данные противоречивы. Для многих типов шин и дорожных покрытий в литературе указываются значения коэффициента поперечного сцепления как больше, так и меньше коэффициента . Поэтому при отсутствии точных данных о коэффициенте для конкретного ДТП наиболее целесообразно в экспертных расчетах принимать для случая движения автомобиля накатом 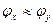. При движении автомобиля под действием тяговых или тор­мозных сил в контактах шин с дорогой действуют зна­чительные продольные реакции, и для поперечной устой­чивости может быть использована только часть сцеп­ления. Соответственно снижается и критическая скорость по условиям поперечного скольжения

,

где х — коэффициент тормозной (или тяговой) силы, равный отношению тормозной (или тяговой) силы к весу, прихо­дящемуся на колесо.

При полной блокировке колеса и опасность возникновения заноса становится реальной. Иногда эксперты, определяя скорость для тормозного режима, не вычисляют коэффициента x, а уменьшают значение коэффициента поперечного скольжения, принимая 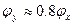. Однако такой прием вряд ли можно считать оправданным. Скорость, максимально допустимая по условиям опрокидывания автомобиля,

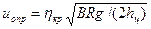(6.5)

где — коэффициент, учитывающий поперечный крен под­рессоренных масс (кузова) автомобиля на упругих эле­ментах подвески под действием центробежной силы. Для легковых автомобилей = 0,8...0,9, для грузовых авто­мобилей и автобусов = 0,85...0,95.

При скорости колеса одной стороны автомобиля отрываются от дороги, однако это не всегда приводит к опрокидыванию автомобиля. Например, на аттракционах типа автородео натренированные водители могут вести автомобиль на двух колесах довольно долго (мировой рекорд в этом виде спорта превышает 20 км). Однако в эксплуатационных условиях водитель часто не успе­вает снизить скорость или повернуть рулевое колесо и опрокидывание автомобиля становится неизбежным.

Расстояние R не следует отождествлять с радиусом закругления дороги р. Автомобиль может весьма круто повернуть на прямом участке дороги, а на закруглении дороги, напротив, двигаться прямолинейно. Считать, что кривизна траектории заднего моста совпадала с кри­визной дороги можно только в том случае, если водитель не совершал резких маневров и вел автомобиль парал­лельно оси дороги. Радиус определяют по планам местности, имеющимся в материалах дела. При опре­делении его на месте ДТП нужно рулеткой наметить хорду АВ (рис. 6.1) и на середине ее (в точке С) за­мерить высоту сегмента y₁. Тогда радиус закругления

где — длина полухорды АС.

Таким же образом можно определить радиус , если на дороге остались отчетливые следы качения, кривизна которых примерно постоянна. Если кривизна следов заметно изменяется, что свидетельствует о повороте рулевого колеса водителем, то радиус характеризует кривизну траектории только в одной ее точке.

Движение автомобиля по кривой постоянного радиуса также как строго прямолинейное движение, является частным, предельным случаем и практически встречается редко. Гораздо чаще автомобиль движется по дуге пере­менного радиуса, уменьшающегося или увеличиваю­щегося. Такие переходные кривые обязательно сопут­ствуют любому изменению направления движения. Автомобиль не может мгновенно перейти от прямолинейного движения к движению по дуге постоянной кри­визны. Между этими двумя фазами всегда имеется движение по переходной кривой.

Рассмотрим этот процесс более подробно.

Рис. 6.1. Определение радиуса кривизны траектории

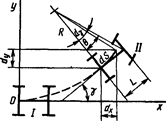
Рис. 6.2. Схема поворота авто­мобиля

На рис. 6.2 цифрой I отмечено положение автомобиля в начальный момент его криволинейного движения, когда передние колеса еще находятся в нейтральном поло­жении (угол их поворота равен нулю). Проведем прямо­угольную систему координат так, чтобы ее начало совпа­дало с серединой заднего моста автомобиля, а ось ОХ — с его продольной осью в положении I. В момент вре­мени t = 0 водитель начинает поворачивать передние колеса и движение автомобиля становится криволиней­ным. После поворота колес на некоторый угол 9 (поло­жение II) автомобиль повернется относительно оси ОХ на угол у (курсовой угол). У автомобиля с жесткими шинами вектор скорости центра колеса совпадает с его плоскостью, поэтому можно написать

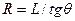(6.6)

Для опасных ситуаций, предшествующих ДТП, харак­терен дефицит времени, при котором водитель не успе­вает повернуть рулевое колесо на большой угол. В табл. 6.1 приведены примерные значения максималь­ного угла , полученные при испытаниях автомобиля ГАЗ-24 «Волга».

Согласно данным таблицы угол при экстренном маневрировании не превышает 5°, что позволяет считать и написать

(6.7)

После поворота автомобиля еще на бесконечно малый угол середина заднего моста опишет элементарную

дугу , равную 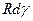. При движении автомобиля с по­стоянной скоростью 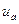длина дуги . С учетом равенства (6.7)

Закон изменения угла по времени зависит от води­теля и в обычных эксплуатационных условиях может быть весьма разнообразным. Однако эксперименталь­ными исследованиями установлено, что в опасных дорож­ных ситуациях водитель, стремясь предотвратить ДТП, поворачивает рулевое колесо весьма резко, но на не­большой угол. При этом угловая скорость поворота передних колес практически постоянна () И угол изменяется примерно пропорционально времени:

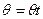При этом допущении курсовой угол у прямо про­порционален квадрату времени:

(6.8)

При небольших значениях угла и коротких проме­жутках времени, характерных для опасных ДТС, кур­совой угол обычно составляет 10—12°. Для таких малых углов можно принять cos γ = 1 и sinγ=γ. Тогда при­ращения и координат х и у за бесконечно малый промежуток времени . Следовательно, координаты середины заднего моста (точка В) в момент времени:

(6.9)

(6.10)

Формулы (6.8) — (6.10) позволяют найти коорди­наты Хв и Yв середины заднего моста и курсовой угол в любой момент времени и определить по ним положение каждой точки автомобиля в процессе входа его в поворот при < 15° = 0,216 рад.

Таблица 6.1. Максимальные углы поворота передних колес при экстренном маневрировании, град

Состояние асфальтобетонного покрытия	Скорость движения, км/ч
11,1	16,7	22,2
Сухое Мокрое	4,8 4,6	4,5 3,8	4,2 3,4

Подставив в выражение (6.10) значение из фор­мулы (6.9), получаем уравнение траектории середины заднего моста (точка В):

(6.11)

Таким образом, при равномерном движении авто­мобиля и повороте передних колес с постоянной угловой скоростью траектория представляет собой кубическую параболу. Поэтому при проектировании и строительстве автомобильных дорог кривые переменного радиуса часто выполняют в виде кубической параболы.

После окончания поворота колес (через время ) курсовой угол автомобиля

Координаты точки В в этот момент: ;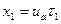

Дата добавления: 2015-10-16