Теорема сложения вероятностей. Условная вероятность. Теорема умножения вероятностей. Независимые события

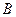Опр. Суммой двух событий и называется событие , состоящее в наступлении хотя бы одного из событий.

Если и 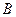- совместные события, то их сумма обозначает наступление или события , или события 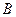, или обоих событий вместе.

Если и 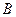- несовместные события, то их сумма означает наступление или события , или события .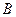

Опр. Произведением двух событий и 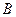называется событие, состоящее в совместном наступлении обоих событий.

Если и 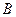- совместные события, то их произведение обозначает наступление и события , и события .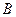

Теорема. (Теорема сложения вероятностей несовместных событий).

Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

. (6)

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

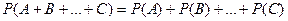. (7)

Следствие. Сумма вероятностей событий, образующих полную группу, равна единице:

(8)

Следствие. Сумма вероятностей противоположных событий равна единице:

. (9)

При совместном рассмотрении двух случайных событий и 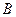часто возникает вопрос: насколько связаны эти события друг с другом, в какой мере наступление одного из них влияет на возможность наступления другого?

Простейшим примером связи между двумя событиями может служить причинная связь – когда наступление одного из событий ведет к обязательному осуществлению другого или же, наоборот, когда наступление одного исключает шансы другого. Скажем, если событие заключается в том, что выбранное наугад изделие данного предприятия не содержит брака, а событие 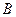– в том, что изделие является первосортным, то ясно, что наступление 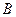влечет за собой в обязательном порядке наступление ; напротив, событие исключает событие .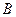

Однако наряду с такими крайними случаями существует и много промежуточных, когда непосредственная причинная зависимость одного события от другого отсутствует, но некоторая зависимость все, же имеется.

Для характеристики зависимости одних событий от других вводится понятие условной вероятности.

Опр. Пусть и 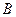– два случайных события по отношению к некоторому опыту, причем, Число называется вероятностью события при условии, что наступило событие 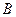, или, просто условной вероятностью события .

Вероятность при условии 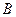обозначается или . Таким образом, по определению имеем следующее равенство:

или

.

Теорема. (Теорема умножения вероятностей зависимых событий).

Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:

, или (10)

Сравнивая эти равенства, мы видим, что

Опр. Говорят, что событие не зависит от 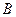, если выполняется равенство

(11)

Другими словами, события называются независимыми, если появление одного из них не меняет вероятности наступления другого.

Имеет место теорема о произведении независимых событий.

Теорема. (Теорема умножения вероятностей независимых событий).

Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

(12)

Теорема. (Теорема сложения вероятностей совместных событий).

Вероятность появления хотя бы одного из двух совместных событий, равна сумме вероятностей этих событий без вероятности их совместного появления:

. (13)

Пример 6. В первом ящике 2 белых и 10 черных шаров, во втором 8 белых и 4 черных. Из каждого ящика вынули по шару. Найдите вероятность того, что они оба белые.

Решение.

Пусть событие - вынут белый шар из первого ящика, событие 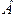- вынут белый шар из второго ящика. События и 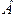- независимые и совместные, тогда согласно формуле 12, получаем:

Ответ: .

Пример 7. Вероятность попадания первого стрелка равна 0,8, а второго 0,9. Производится залп. Найдите вероятность того, что в мишени одна пробоина.

Решение.

Введем события:

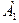- первый попал, ;

- первый промахнулся, ;

- второй попал, ;

- второй промахнулся, .

Выпишем полную группу событий:

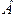- в мишени пробоин нет (оба промахнулись, т.е. );

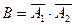- в мишени одна пробоина (один попал, при этом другой промахнулся, т.е. );

- в мишени две пробоины (попали оба, т.е. ).

Решить можно двумя способами.

1 способ.

2 способ. (Через противоположное событие)

Ответ: 0,26.

Теорему умножения вероятностей легко обобщить на любое конечное число событий.

Теорема. Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих каждому из них событий, т.е.

. (14)

Пример 8. На десяти карточках напечатаны цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Найдите вероятность того, что три наудачу взятые и поставленные в ряд карточки составят число 125.

Решение.

Искомое событие произойдет, если первой будет взята карточка с цифрой 1 (событие ), вторая – с цифрой 2 (событие 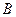), третья – с цифрой 5 (событие ). Вероятность его по теореме умножения вероятностей для трех зависимых событий:

.

Ответ: 0,0014. [3, с.48-51]

Дата добавления: 2015-10-16