Формула Пуассона

Но в жизни встречаются задачи, когда 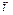и - велики, а 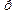- мало. Например, Ясно, что в этом случае воспользоваться формулой Бернулли технически очень сложно. Возникает необходимость в желании иметь более простые приближенные формулы для вычисления вероятности при больших 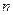. Такие формулы, называемые асимптотическими, существуют и определяются теоремой Пуассона, локальной и интегральной теоремами Муавра-Лапласа. Наиболее простоя из них является теорема Пуассона.

При больших 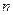и малых 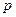имеет место теорема.

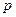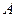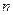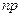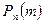Теорема. Если вероятность наступления события в каждом испытании стремится к нулю при неограниченном увеличении числа испытаний , причем произведение стремиться к постоянному числу то вероятность того, что событие 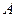появится т раз в 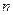независимых испытаниях, удовлетворяет предельному равенству

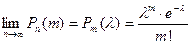
Итак, если вероятность 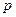– постоянна и мала, число испытаний 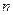– велико и число 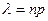- незначительно (). То из предельного равенства вытекает приближенная формула Пуассона:

(23)

Функция Пуассона табулирована (см. таблице 3 приложений [4, с.556]), но можно воспользоваться и значениями:

….

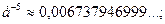
Пример 12. На факультете насчитывается 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета?

Решение.

Из условия задачи следует, что , , .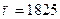

Найдем , т. е. условие - выполняется, можно воспользоваться формулой 23 и таблицей 3 «Значения функции Пуассона»:

.

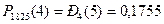Ответ: 0,1755. [4, с.72-73]

Дата добавления: 2015-10-16