Геометрическое определение вероятности

Одним из недостатков классического определения вероятности (1), ограничивающим его применение, является то, что оно предполагает конечное число возможных исходов испытания.

Оказывается, иногда этот недостаток можно преодолеть, используя геометрическое определение вероятности, т.е. находя вероятность попадания точки в некоторую область (отрезок, часть плоскости и т.п.).

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Если предположить, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок определяется равенством

. (3)

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Если предположить, что вероятность попадания брошенной точки на фигуру пропорциональна площади этой фигуры и не зависит ни от её расположения относительно G, ни от формы g, то вероятность попадания точки в фигуру g определяется равенством

(4)

Аналогично определяется вероятность попадания точки в пространственную фигуру v, которая составляет часть фигуры V:

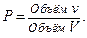(5)

Причём, отрезок l, фигура g, пространственная фигура v называются благоприятствующими (благоприятными) событию.

Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (отрезок), двумерной (фигура на плоскости), трёхмерной (некоторое тело в пространстве). Обозначая меру (длину, площадь, объём) области через , приходим к следующему определению.

Опр. Геометрической вероятностью события называется отношение меры области, благоприятствующей появлению событию , к мере всей области, т.е.

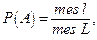(3*)

(4*)

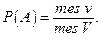(5*)

Пример 5. Два лица и 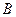условились встретиться в определённом месте, договорившись лишь о том, что каждый является туда в любой момент времени между 11 и 12 ч и ждёт в течение 30 мин. Если партнёр к этому времени не пришёл или уже успел покинуть установленное место, встреча не состоится. Найти вероятность того, что встреча состоится.

Решение

Обозначим моменты прихода в определённое место лиц и 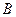соответственно через x и y. В прямоугольной системе координат 0ху возьмём за начало отсчёта 11 ч, а за единицу измерения 1 ч. По условию , . Этим неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату OKLM со стороной, равной 1 (рис. 1).

у

1 К L

G g

0,5

С

М

0 0,5 1 х

Рис. 1. Геометрическое представление решения примера 5.

Событие – встреча двух лиц – произойдёт, если разность между и у не превзойдёт 0,5 ч. (по абсолютной величине), т.е.

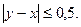
Решение последнего неравенства есть полоса

которая внутри квадрата на рис. 1 представляет заштрихованную область g.

По формуле (4)

так как площадь области g равна площади квадрата G без суммы двух угловых (незашрихованных) треугольников.

Ответ: 0,75. [4, с.22-24]

Дата добавления: 2015-10-16