Формула полной вероятности. Формула Байеса

Следствием двух основных теорем теории вероятностей – теоремы сложения и теоремы умножения – являются формула полной вероятности и формула Байеса

Предположим, что событие 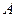может наступить только вместе с одним из нескольких попарно несовместных событий .Условимся называть эти события (по отношению к 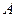) гипотезами. Имеет место следующая теорема.

Теорема. Вероятность события 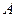, которое может наступить лишь при условии появления одного из несовместных событий (гипотез) , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события :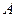

(17)

В тесной связи с формулой полной вероятности находится так называемая формула Байеса. Она относится к той ситуации, что и формула полной вероятности (событие 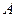может наступить только вместе с одним из 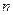попарно несовместных событий ). Формула Байеса решает следующую задачу.

Пусть произведен опыт, в результате него наступило событие 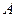. Сам по себе, этот факт еще не позволяет сказать, какое из событий , имело место в проделанном опыте. Можно, однако, поставить такую задачу: найти вероятности

…

каждой из гипотез в предположении, что наступило событие 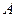. Эту задачу и решает как раз формула Байеса:

. (18) [4, с.51-52]

Пример 9. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого вдвое больше производительности второго. Первый в среднем производит 60% деталей отличного качества, второй – 84%. Найдите: а) наудачу взятая с конвейера деталь оказалась отличного качества; б) вероятность того, что наудачу взятая с конвейера деталь отличного качества изготовлена на первом автомате.

Решение.

Обозначим событие - взятая случайным образом деталь – отличного качества.

Возможны следующие гипотезы: - деталь изготовлена на первом автомате, 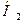- деталь изготовлена на втором автомате. Так как производительность первого вдвое больше производительности второго, то и .

Условная вероятность того, что взятая деталь отличного качества, изготовлена на первом автомате будет равна (т.к. первый в среднем производит 60% деталей отличного качества).

Условная вероятность того, что взятая деталь отличного качества, изготовлена на втором автомате будет равна (т.к. второй в среднем производит 84% деталей отличного качества).

а) Вероятность того, что наудачу взятая с конвейера деталь оказалась отличного качества находим по формуле полной вероятности

.

б) Вероятность того, что наудачу взятая с конвейера деталь отличного качества изготовлена на первом автомате, находим по формуле Байеса

Ответ: а) 0,68; б)

Дата добавления: 2015-10-16