Введение. Задача любой науки состоит в выявлении и исследовании закономерностей

Задача любой науки состоит в выявлении и исследовании закономерностей, которым подчиняются реальные процессы.

Ранее закономерности мы описывали с помощью функции. Функциональная связь между переменными являлась «жёсткой»: значение одной из них вполне определялось значением другой. Однако часто приходится изучать явления, для которых практически трудно или принципиально невозможно отыскать все причины, порождающие их, и тем более, количественно их выразить. Такие явления невозможно описать функционально.

Например, при бросании монеты нельзя предсказать, какой стороной она упадёт; для этого необходимо было бы учесть слишком много различных факторов: работу мышц руки, участвующей в бросании, малейшие отклонения в распределении массы монеты, движение воздуха и т.д. Результат бросания монеты случаен. Но, оказывается, при достаточно большом числе бросаний монеты существует определённая закономерность (герб и цифра выпадают приблизительно поровну).

Теория вероятностей – математическая наука, изучающая закономерности случайных явлений.

Под случайными явлениями понимаются явления с неопределённым исходом, происходящие при неоднократном воспроизведении определённого комплекса условий.

Очевидно, что в природе, технике и экономике нет явлений, в которых не присутствовали бы элементы случайности. Существуют два подхода к изучению этих явлений. Один из них – классический, или «детерминистский», состоит в том, что выделяются основные факторы, определяющие данное явление, а влиянием множества остальных, второстепенных факторов, приводящих к случайным отклонениям его результата, пренебрегают. Таким образом, выявляется основная закономерность, свойственная данному явлению, позволяющая однозначно предсказать результат по данным условиям. Этот подход часто используется в естественных («точных») науках.

При исследовании многих явлений и, прежде всего, социально-экономических, такой подход неприемлем. В этих явлениях необходимо учитывать не только основные факторы, но и множество второстепенных, приводящих к случайным возмущениям и искажениям результата, т.е. вносящих в него элемент неопределённости. Поэтому другой подход к изучению явлений состоит в том, что элемент неопределённости, свойственный случайным явлениям и обусловленный второстепенными факторами, требует специальных методов их изучения. Разработкой таких методов, изучением специфических закономерностей, наблюдаемых в случайных явлениях, и занимается теория вероятностей.

Первые работы, в которых зарождались основные понятия теории вероятностей, появились в XVI-XVII вв. Они принадлежали Д. Кардано, Б. Паскалю, П. Ферма, Х. Гюйгенсу и др. и представляли попытки создания теории азартных игр с целью дать рекомендации игрокам. Следующий этап развития теории вероятностей связан с именем Я. Бернулли (XVII – начало XVIII в.), который доказал теорему, теоретически обосновавшую накопленные ранее факты и названную в дальнейшем «законом больших чисел».

Дальнейшее развитие теории вероятностей приходится на XVII-XIX вв. благодаря работам А. Муавра, П. Лапласа, К. Гаусса, С. Пуассона и др. Весьма плодотворный период развития «математики случайного» связан с именами русских математиков П.Л. Чебышева, А.М. Ляпунова и А.А. Маркова (XIX-начало ХХ в.).

Большой вклад в последующее развитие теории вероятностей и математической статистики внесли российские математики: С.Н. Бернштейн, В.И. Романовский, А.Н. Колмогоров, А.Я. Хинчин, Ю.В. Линник, Б.В. Гнеденко, Н.В. Смирнов, Ю.В. Прохоров и др., а также учёные англо-американской школы Стьюдент (псевдоним В. Госсета), Р. Фишер, Э. Пирсон, Е. Нейман, А. Вальд и др. Особо следует отметить неоценимый вклад академика А.Н. Колмогорова в становлении теории вероятностей как математической науки. [4, с.12-14]

Глава 1. Основные понятия и теоремы теории вероятностей

Основные понятия

В любой науке есть основные понятия, на которые она опирается. Каждое последующее понятие определяется через предыдущие. Но где-то этот процесс определений должен заканчиваться. В «истоке» должны быть первоначальные понятия, которые нельзя определить через другие, они лишь разъясняются, а все остальные сводятся к ним. К таким понятиям в теории вероятностей относятся событие и равновозможность.

Опр. Под испытанием (опытом, экспериментом) понимается выполнение определённого комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат. Испытание (опыт) может быть осуществлено человеком, но может проводиться и независимо от человека, выступающего в этом случае в роли наблюдателя.

Испытаниями, например, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесёнными на каждую грань числом очков – от одного до шести).

Опр. Случайным событием (возможным событием или просто событием) называется любой факт, который в результате испытания может произойти или не произойти.

Событиями являются: «выпадение герба или цифры», «попадание в цель» или «промах», появление того или иного числа очков на брошенной игральной кости.

Событие – это не какое-нибудь происшествие, а лишь возможный исход, результат испытания (опыта, эксперименты). События обозначаются прописными (заглавными) буквами латинского алфавита: А, В, С и т.д.

Если при каждом испытании, при котором происходит событие А, происходит и событие В, то говорят, что А влечёт за собой событие В (входит в В) или В включает событие А и обозначают А 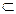В. Например, если событие А – изделие 1-го сорта, В – изделие 2-го сорта, С – изделие стандартное, то А 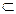С и В 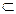С (та как изделия 1-го и 2-го сорта - стандартные).

Опр. Если одновременно А 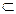В и В 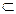А, то в этом случае события А и В называются равносильными.

Опр. Два события называются совместимыми (совместными), если появление одного из них не исключает появление другого в одном и том же испытании.

Опр. Два события называются несовместимыми (несовместными), если появление одного из них исключает появление другого в одном и том же испытании.

Например, выигрыш по одному билету денежно-вещевой лотереи двух ценных предметов – события несовместные, а выигрыш тех же предметов по двум билетам – события совместные. Получение студентом на экзамене по одной дисциплине оценок «отлично», «хорошо» и «удовлетворительно» - события несовместимые, а получение тех же оценок на экзаменах по трём дисциплинам – события совместные.

Несовместимость более чем двух событий означает их попарную несовместимость.

Опр. Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.

Событие, противоположное событию , обозначается . Например, «появление герба» и «появление решки» при подбрасывании монеты, «отсутствие бракованных изделий» и «наличие хотя бы одного бракованного изделия» в партии – события противоположные.

Опр. Событие называется достоверным, если в результате испытания оно обязательно должно произойти.

Опр. Событие называется невозможным, если в результате испытания оно вообще не может произойти.

Например, если в партии все изделия стандартные, то извлечение из неё стандартного изделия – событие достоверное, а извлечение при тех же условиях бракованного изделия – событие невозможное.

Опр. События называются равновозможными, если в результате испытания по условиям симметрии ни одно из этих событий не является объективно более возможным.

Например, «извлечение туза, валета, короля или дамы» из колоды карт, либо «появление герба» или «появление решки» при подбрасывании монеты – события равновозможные. Так, если монета «правильная», выполнена симметрично, то нет никаких оснований считать «появление герба» при подбрасывании монеты событием объективно более возможным, чем «появление решки».

Опр. Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти хотя бы одно из них.

Например, события, состоящие в том, что в семье из двух детей: А – «два мальчика», В – «один мальчик, одна девочка», С – «две девочки» - являются единственно возможными.

Опр. Несколько событий образуют полную группу (полную систему), если они являются единственно возможными и несовместными исходами испытания. То есть, в результате испытания обязательно должно произойти одно и только одно из этих событий.

Например, «выпадение герба» и «выпадение решки» при одном подбрасывании монеты; «попадание в цель» и «промах» при одном выстреле; «выпадение одного, двух, трёх, четырёх, пяти и шести очков» при одном подбрасывании игральной кости. [3, с.40-42]

Дата добавления: 2015-10-16