Классическое определение вероятности

Для практической деятельности важно уметь сравнивать события по степени возможности их поступления. Очевидно, события: «выпадение дождя» и «выпадение снега» в первый день лета в данной местности, «выигрыш по одному билету» и «выигрыш по одному из n приобретённых билетов» денежно-вещевой лотереи – обладают разной степенью возможности их наступления. Поэтому для сравнения событий нужна определённая мера.

Опр. Численная мера степени объективной возможности наступления события называется вероятностью события.

Это определение, качественно отражающее понятие вероятности события, не является математическим. Чтобы оно таким стало, необходимо определить его количественно.

Опр. События, образующие полную группу, т.е. события единственно возможные, несовместные и равновозможные, будем называть элементарными событиями (исходами, случаями, шансами).

Опр. Событие называется благоприятствующим (благоприятным) событию В, если появление события А влечёт за собой появление события В.

Опр. (Классическое определение вероятности).

Вероятность события равна отношению числа случаев (исходов), благоприятствующих ему, к общему числу случаев (исходов), т.е.

(1)

где

Р(А) – вероятность события А;

m – число случаев (исходов), благоприятствующих событию А;

n – общее число случаев (исходов).

Классическое определение (точнее, классическая формула) вероятности (1) долгое время, с XVII вплоть до XIX вв., рассматривалась действительно как определение вероятности, так как в то время методы теории вероятностей применялись в основном к азартным играм, которые сводились к схеме случаев, или в задачах, которые искусственно сводились к этой схеме. В настоящее время формальное определение вероятности не даётся (это понятие считается первичным и не определяется), а при его пояснении используют понятие относительной частоты события (см. ниже 1.3).

Поэтому, классическое определение (классическую формулу) вероятности следует рассматривать не как определение, а как метод вычисления вероятностей для испытаний, сводящихся к схеме случаев.

Свойства вероятности события:

1 Вероятность любого события есть положительное число, заключённое между нулём и единицей, т.е.

0 ≤ Р(А) ≤ 1.

2 Вероятность достоверного события равна единице.

3 Вероятность невозможного события равна нулю.

События, вероятности которых очень малы (близки к нулю) или очень велики (близки к единице), называются соответственно практически невозможными или практически достоверными событиями.

Пример 1. Вычислите вероятность выпадения герба при одном бросании монеты.

Решение

Очевидно, событие – «выпадение герба» и событие 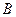– «выпадение решки» – образуют полную группу событий несовместных и равновозможных, т.е. 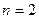. Событию благоприятствует лишь одно событие – само , здесь 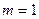. Поэтому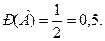

Ответ: 0,5.

Пример 2. При бросании игральной костивозможны шесть исходов – выпадение 1, 2, 3, 4, 5, 6 очков. Какова вероятность появления чётного числа очков?

Решение

Все 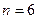исходов образуют полную группу событий и равновозможны, т.е. единственно возможны, несовместны и равновозможны. Событию – «появление чётного числа очков» благоприятствуют 3 исхода (случая) – 2, 4, 6 очков. Тогда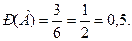

Ответ: 0,5. [4, с.18-20]

Дата добавления: 2015-10-16