Вероятность хотя бы одного события

Вероятность появления хотя бы одного из попарно независимых событий

А ₁, А ₂,…, А_п равна

р (А) = 1 – q ₁ q ₂… q_n, (2.9)

где q_i – вероятность события , противоположного событию А_i.

Доказательство.

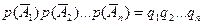Если событие А заключается в появлении хотя бы одного события из А ₁, А ₂,…, А_п, то события А и противоположны, поэтому по теореме 2.2 сумма их вероятностей равна 1. Кроме того, поскольку А ₁, А ₂,…, А_п независимы, то независимы и , следовательно, р () = . Отсюда следует справедливость формулы (2.9).

Пример. Сколько нужно произвести бросков монеты, чтобы с вероятностью не менее 0,9 выпал хотя бы один герб?

Решение. Вероятность выпадения герба при одном броске равна вероятности противопо-ложного события (выпадения цифры) и равна 0,5. Тогда вероятность выпадения хотя бы одного герба при п выстрелах равна 1- (0,5) ^п. Тогда из решения неравенства 1- (0,5) ^п > 0,9

следует, что п > log₂10 ≥ 4.

Дата добавления: 2015-10-21