Центральная предельная теорема

Закон больших чисел не исследует вид предельного закона распределения суммы случайных величин. Этот вопрос рассмотрен в группе теорем, называемых центральной предельной теоремой. Они утверждают, что закон распределения суммы случайных величин, каждая из которых может иметь различные распределения, приближается к нормальному при достаточ-но большом числе слагаемых. Этим объясняется важность нормального закона для практичес-ких приложений.

Характеристические функции.

Для доказательства центральной предельной теоремы используется метод характеристичес-ких функций.

Определение 14.1. Характеристической функцией случайной величины Х называется функция

g (t) = M (e^itX) (14.1)

Таким образом, g (t) представляет собой математическое ожидание некоторой комплексной случайной величины U = e^itX, связанной с величиной Х. В частности, если Х – дискретная случайная величина, заданная рядом распределения, то

. (14.2)

Для непрерывной случайной величины с плотностью распределения f (x)

(14.3)

Пример 1. Пусть Х – число выпадений 6 очков при одном броске игральной кости. Тогда по формуле (14.2) g (t) =

Пример 2. Найдем характеристическую функцию для нормированной непрерывной случайной величины, распределенной по нормальному закону 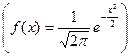. По формуле (14.3) (использовалась формула 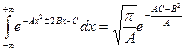и то, что i ² = -1).

Дата добавления: 2015-10-21