Предельные формула. Локальная формула Лапласса. Интегральная формула Лапласса. Формула Пуассона

Локальная теорема Муавра-Лапласа. Если вероятность появления события А в каждом из n 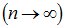независимых испытаний равна одной и той же постоянной р =const (0< р <1), то вероятность 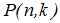того, что во всех этих испытаниях событие А появится ровно k раз, приближенно вычисляется формулой:

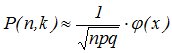, (4.8)

где: , 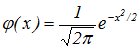-- кривая Гаусса.

Таблицы значений функции даны в приложениях к учебникам по теории вероятностей

Интегральная теорема Муавра-Лапласа. Пусть вероятность появления события А в каждом из n (n →∞)независимых испытаний равна одной и той же постоянной р (0< р <1), то вероятность 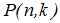того, что во всех этих испытаниях событие А появится не менее k ₁ и не более k ₂ раз, приближенно вычисляется формулой:

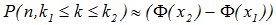, (4.9)

где

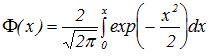- функция Лапласа,

,

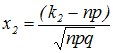
Значения аргументов функции Лапласа для х Î[0,5] даны в приложениях к учебникам по теории вероятностей (Приложение 2 настоящего методического пособия), для x>5 F(x)=1/2.Функция нечетная - F(x)= F(-x).

Формула Бернулли требует громоздких расчетов при большом количестве испытаний. Можно получить более удобную для расчетов приближенную формулу, если при большом числе испытаний вероятность появления А в одном опыте мала, а произведение пр = λ сохраняет постоянное значение для разных серий опытов (то есть среднее число появле-ний события А в разных сериях испытаний остается неизменным). Применим формулу Бернулли:

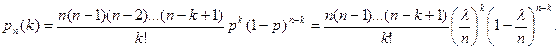
Найдем предел полученного выражения при

Таким образом, формула Пуассона

(3.4)

позволяет найти вероятность к появлений события А для массовых (п велико) и редких (р мало) событий.

Дата добавления: 2015-10-21