Читайте также:
|
Сфера радиуса 
с центром в начале координат
Эллипсоид с полуосями 
и центром в начале координат
При 
эллипсоид превращается в сферу радиуса .
Однополостный гиперболоид с полуосями и осью 
(рисунок 98)
Сечения гиперболоида горизонтальными плоскостями 
являются эллипсами: 
.
Сечения гиперболоида вертикальными плоскостями 
или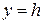 
являются гиперболами: 
или 
.
Двуполостный гиперболоид с полуосями и осью 
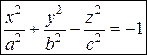
Сечения гиперболоида горизонтальными плоскостями , 
являются эллипсами: 
.
Сечения гиперболоида вертикальными плоскостями или 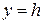являются гиперболами: 
или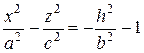 
.
Параболоид эллиптический с параметрами 
и вершиной в начале координат
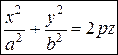Сечения параболоида горизонтальными плоскостями (
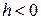при 
, 
при 
) являются эллипсы: 
.
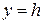Сечения параболоида вертикальными плоскостями или являются параболами: 
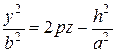или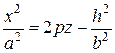 
.
Параболоид гиперболический с параметрами и вершиной в начале координат (рисунок 101)
Сечения параболоида горизонтальными плоскостями представляют собой гиперболы: 
.
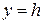Сечения вертикальными плоскостями или являются параболами: 
или 
.
Конус эллиптический с вершиной в начале координат и осью
Эллиптический цилиндр: 
Если 
, то цилиндр круговой 
.
Гиперболический цилиндр: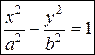 
Список литературы
1. Аксёнов, А. П. Математический анализ. (Интегралы, зависящие от параметра. Двойные интегралы. Криволинейные интегралы): Учебное пособие. – СПб.: НЕСТОР, 2000. – 145 с.
2. Аксёнов, А. П. Математический анализ. (Ряды Фурье. Интеграл Фурье. Суммирование расходящихся рядов.) Учебное пособие. – СПб.: НЕСТОР, 1999. – 86 с.
3. Алексеев, В. Б. Теорема Абеля в задачах и решениях. – М.: МЦНМО, 2001. – 192 с.
4. Арнольд, В. И. Геометрия комплексных чисел, кватернионов и спинов. – М.: МЦНМО, 2002. – 40 с.
5. Артамонов, В. А. Лекции по алгебре. 1 семестр. – М.: МГУ, 2000 – 63 с.
6. Будылин, А. М. Ряды и интегралы Фурье / А. М. Будылин. – М. 2002. – 127 с.
7. Булгаков, Н. А. Основные законы и формулы по математике и физике: школьная математика, высшая математика, физика. – Тамбов: ТГТУ, 2002. – 59 с.
8. Гантмахер, Ф. Р. Теория матриц [Текст]. – Изд. 2-е, дополн. / Ф.Р. Гантмахер. – М. 1966. – 576 с.
9. Ильин, В. А. Математический анализ. Начальный курс / В.А. Ильин, В.А. Садовничий, Бл.X. Сендов / под ред. А.Н. Тихонова. – 2-е изд., перераб. - М.: МГУ, 1985. – 662 с.
10. Ильин, В. А. Математический анализ. Продолжение курса / В.А. Ильин, В.А. Садовничий, Бл.X. Сендов / под ред. А.Н. Тихонова. – М.: МГУ, 1987. – 358 с.
11. Картан, А. Дифференциальное исчисление. Дифференциальные формы [Текст]: Пер. с фр. / Под ред. Б.А. Фукса. – М. 1971. – 393 с.
12. Коддингтон, Э. А. Теория обыкновенных дифференциальных уравнений [Текст] / Э.А. Коддингтон, Н. Левинсон: пер. с англ. – М. 1958. – 475 с.
13. Кострикин, А. И. Линейная алгебра и геометрия [Текст] / А.И. Кострикин, Ю.И. Манин. – Москва, 1980. – 309 с.
14. Кудрявцев, Л. Д. Курс математического анализа: в 3 т.: учебник для студентов университетов и втузов. – М.: Высш. школа, 1981 – Т.1. – 687 с.
15. Кудрявцев, Л. Д. Курс математического анализа: в 3 т: учебник для студентов университетов и втузов. – М.: Высшая школа, 1981 – Т.2. – 584 с.
16. Кудрявцев, Л. Д. Курс математического анализа: учебник для студентов университетов и вузов: в 3 т. – Т.3. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1989. – 352 с.
17. Курош, А. Г. Курс высшей алгебры [Текст]. – Изд. 9-е. – М., 1968. – 431 с.
18. Курош, А. Г. Общая алгебра / А. Г. Курош. – М., 1973. – 162 с.
19. Начало математического анализа: учеб.-метод. пособие / Авт.-сост.: А.Я. Алеева, Ю.Ю. Громов, О.Г. Иванова, А.В. Лагутин. – Тамбов: Изд-во ТГТУ, 2001. – 56 с.
20. Носов, В. А. Комбинаторика и теория графов: учебное пособие / В. А. Носов – М., 1999. – 116 с.
21. Острик, В. В., Цфасман, М. А. Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые. (Серия: "Библиотека "Математическое просвещение") / Под ред. В.М. Тихомирова. – М.: МЦНМО, 2001. – 48 с.
22. Полиа, Г. Задачи и теоремы из анализа. Часть 1. Ряды. Интегральное исчисление. Теория функций. 3-е изд.: Пер. с нем. Полиа Г., Сеге, Г. Д. А. Райкова. – М.: Наука, 1978. – 392 с.
23. Полиа, Г. Задачи и теоремы из анализа. Часть 2. Теория функций (специальная). Распределение нулей. Полиномы. Определители. Теория чисел. 3-е изд. /: Пер. с нем. Д.А. Райкова. – М.: Наука, 1978. – 432 с.
24. Понтрягин, Л. С. Обыкновенные дифференциальные уравнения [Текст]. – Изд. 4-е. – М., 1974. – 331 с.
25. Преображенский, С. П., Тихомиров, С. Р. Интегрирование дифференциальных уравнений с помощью степенных рядов. – М., 1987. – 15 с.
26. Проскуряков, И. В. Сборник задач по линейной алгебре. – М., 1966. – 381 с.
27. Титчмарш, Е. Теория функций: пер. с англ. – 2-е изд. перераб. – М.: Наука. Главная редакция физико-математической литературы, 1980. – 464 с.
28. Тихомиров, В. М. Дифференциальное исчисление (теория и приложения). – М.: МЦНМО, 2002. – 40 с.
29. Филиппов, А. Ф. Сборник задач по дифференциальным уравнениям. – Ижевск: НИЦ "Регулярная и хаотичная динамика", 2000. – 176 с. (Серия: "Библиотека "Математическое просвещение")
30. Шилов, Г.Е. Математический анализ [Текст]: Специальный курс / Г. Е. Шилов. – Изд. 2-е. – М., 1961. – 437 с.
Дата добавления: 2015-10-16; просмотров: 65 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Две прямые в пространстве параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, т.е. | | | Немецкий детектив для начального чтения |