Алгоритм Дейкстры

Идея алгоритма построения дерева кратчайших путей и определения их весов, предложен-ного в 1959г. Е. Дейкстрой, такова. На каждом этапе одна новая вершина включается в множес-тво S отмеченных вершин, для которых кратчайшие пути из начальной вершины а уже найде-ны. Тогда на следующем этапе к множеству S добавляется вершина b с самым коротким путем из а, все вершины которого, кроме b,содержатся в S.

Предполагается, что неориентированный граф G = á X, Е ñ содержит n вершин. Без ограни-чения общности можно считать, что все вершины задаются номерами от 0 до n –1 и что началь-ная вершина имеет номер 0. Длина ребра (i, j) между вершинами i и j обозначена через l (i, j); если нет ребра, соединяющего эти вершины, то l (i, j) = ¥. Длина пути L (P) равна сумме длин входящих в него рёбер. Для того, чтобы на рисунках не спутывались длины рёбер и номера вершин, вершины на них обозначены как X0, X1, и т.д. вместо 0, 1, и т.д.

Алгоритм Дейкстры (АД). Рассматриваемый алгоритм основан на расстановке пос- тоянных и временных меток у вершин графа G. Метка является вещественным числом или сим-волом ∞.

Как постоянная, так и временная метка у любой вершины х представляет собой длину не-которого пути из начальной вершины в данную вершину х. Если метка является символом ∞, то это значит, что никакой путь из начальной вершины в данную вершину х ещё не определён. На каждой итерации одна из временных меток становится постоянной и далее уже не меняется (она равна длине искомого кратчайшего пути в данную вершину). Постоянные метки обозначе-ны буквой P, временные - буквой T. Через с обозначена последняя (на данный момент) поме-ченная вершина, через R (x) - вершина, предшествующую вершине x на кратчайшем пути из начальной вершины 0 в вершину x.

Шаг 0 (Инициализация). Положить

P (0) = 0, c = 0, T (x) = ¥ (для всех вершин x ≠ 0); R (x) при инициализации не задаётся, поскольку предшествующие вершины ещё не определены).

Шаг i. Выполнить следующие операции:

А. Для каждой вершины x с временной меткой сделать следующее:

1) положить

Z = P (c) + l (c, x); (1)

2) если Z < T (x), положить T (x) = Z, R (x) = c. В противном случае T (x) и R (x) не меняются.

Б. Найти вершину x с минимальной временной меткой (если несколько вершин имеют од-ну и ту же минимальную временную метку, можно выбрать любую из них); положить c = x; по-ложить в качестве постоянной метки P (с) её временную метку T (с).

В. Если ещё остались вершины с временными метками, положить i = i +1 и перейти к шагу i. В противном случае переходим к шагу F.

Шаг F. На этом шаге определяются кратчайшие пути из начальной вершины 0 во все вершины x ≠0. Кратчайший путь из начальной вершины 0 в любую другую вершину x строится следующим образом: вершиной, предшествующей x на искомом пути, является вершина y = R (x); вершиной, предшествующей y на искомом пути, является вершина z = R (y), и т.д., вплоть до начальной вершины 0. Искомый путь из 0 в x состоит из тех же вершин в обратном порядке ■

При «ручной» реализации АД будет удобно промежуточные результаты записывать в таб-лицу, строки которой соответствуют итерациям, а столбцы (кроме двух левых) – вершинам. В самом левом столбце будем писать номер итерации, а 2-ой слева столбец выделим для записи очередной помечаемой вершины с и её постоянной метки P (с). Каждую клетку в остальных столбцах таблицы разделим на 3 части, в которые будем записывать текущее значение Z, новое значение временной метки Т и новую предыдущую вершину R, или писать старые значения, в зависимости от результата сравнения в пункте 2) шага i -A. После того, как вершина получила постоянную метку, в её клетки ничего не записываем. Числа l (c, x) – длины рёбер – берутся непосредственно из рисунка.

Пример 1. Рассмотрим применение АД для графа, показанного на рис.1. Длины рёбер на-писаны на рисунке прямо около них. Составим вышеупомянутую таблицу.

Рис.1. Граф с длинами рёбер

Таблица 1

Итера- ция

Последняя помеченная

Вершина 0

Вершина 1

Вершина 2

Вершина 3

Вершина 4

Вершина 5

№

с

P

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

Дадим пояснения к заполнению таблицы 1. На 0-ой итерации (инициализации) в соответс-твии с АД начальной вершине 0 присваиваем постоянную метку 0 (оба числа заносятся в 0-ую строку в столбце «Последняя помеченная»). Остальные вершины получают временную метку ∞, которая и заносится в 0-ую строку под буквами T. В остальные позиции 0-ой строки в соот-ветствии с АД ничего не заносится.

На 1-ой итерации обрабатываются только столбцы, соответствующие вершинам, имею-щим временные метки. Таковыми в этот момент являются все вершины, кроме вершины 0. Вы-числяем числа Z для всех этих вершин. Так как на 0-ой итерации с = 0, P (c) = 0, то имеем (см. граф) P (0)+ l (0,1)=1, P (0)+ l (0,2)=5, P (0)+ l (0, х)=∞ для х =3,4,5. Поэтому в 1-ую строку под знаком Z записываются числа 1, 5 и знаки ∞, ∞, ∞. Далее, сравнивая эти значения со значениями T из предыдущей строки, записываем под знаком T в данную строку минимумы, а под знаком R в тех столбцах, где произошли изменения в T – последнюю помеченную вершину изстолбца с (в данном случае 0). Выбирая минимальное значение из записанных значений T, получаем 1 в столбце для вершины 1. Поэтому записываем 1 (номер вершины) под с и 1 (длина кратчайшего пути) под P.

На 2-ой итерации обрабатываются только столбцы, соответствующие вершинам 2, 3, 4 и 5. Так как на 1-ой итерации с =1, P (c)=1, то имеем (см. граф) P (1)+ l (1,2)=9, P (1)+ l (1,3)=11, P (1)+ l (1,4)=7, P (1)+ l (1,5)=∞. Поэтому во 2-ую строку под знаком Z записываются числа 9,11,7 и знак ∞. В клетке справа и сверху от этих чисел записаны (под знаком T) предыдущие временные метки: 5,∞,∞,∞. В клетку во 2-ой строке под знаком T записываем новые временные метки - наименьшие значения из этих двух чисел; получаем 5,11,7 и ∞. Под знаком R в 3-ей и 4-ой группах столбцов во 2-ой строке пишется текущий номер c =1. Выбирая минимальное значение из записанных значений T, получаем 5 в столбце для вершины 2. Поэтому записываем 2 (номер вершины) под с и 5 (длина кратчайшего пути) под P.

На 3-ьей итерации обрабатываются только столбцы, соответствующие вершинам 3,4 и 5. Так как на 2-ой итерации с =2, P (c)=5, то имеем (см. граф) P (2)+ l (2,3)=∞, P (2)+ l (2,4)=12, P (2)+ l (2,5) = ∞. Поэтому в 3-ью строку под знаком Z записываются ∞, 12, ∞. В клетке справа и сверху от этих чисел записаны (под знаком T) предыдущие временные метки: 11, 7,∞. В клетку в 3-ьей строке под знаком T записываем новые временные метки - наименьшие значения из этих пар чисел: 11, 7 и ∞. Под знаком R во всех трёх столбцах ничего не меняется, так как временные метки в них не изменились. Выбирая минимальное значение из записанных значений T, получа-ем 7 в столбце для вершины 4. Поэтому записываем 4 (номер вершины) под с и 7 (длина крат-чайшего пути) под P.

На 4-ой итерации рассматриваются только две вершины: 3 и 5. Новые временные метки для них совпадают. В этом случае можно выбрать любую. Выбираем вершину 3 и в соответст-вии с этим заполняем 4-ую строку и далее – последнюю, 5-ую строку.

Найдём теперь, в соответствии с шагом F АД, сами кратчайшие пути. Просматриваем вершины в том порядке, в каком они идут во 2-ом столбце (в этом порядке они получают посто-янные метки).

Для вершины 1 последнее заполненное значение под знаком R равно 0. Это означает, что предпоследней вершиной на кратчайшем пути из 0 в 1 является начальная вершина 0. Поэтому имеем путь 0→1 длины 1.

Для вершины 2 последнее заполненное значение под знаком R равно 0. Это означает, что предпоследней вершиной на кратчайшем пути из 0 в 2 является начальная вершина 0. Поэтому имеем путь 0→2 длины 5.

Для вершины 4 последнее заполненное значение под знаком R равно 1. Это означает, что предпоследней вершиной на кратчайшем пути из 0 в 4 является вершина 1. Поскольку для вер-шины 1 кратчайший путь таков: 0→1, то имеем путь 0→1→4 длины 7.

Для вершины 3 последнее заполненное значение под знаком R равно 1. Это означает, что предпоследней вершиной на кратчайшем пути из 0 в 3 является вершина 1. Поскольку для вер-шины 1 кратчайший путь таков: 0→1, то имеем путь 0→1→3 длины 11.

Для вершины 5 последнее заполненное значение под знаком R равно 4. Это означает, что предпоследней вершиной на кратчайшем пути из 0 в 5 является вершина 4. Поскольку для вер-шины 4 кратчайший путь таков: 0→1→4, то имеем путь 0→1→4→5 длины 11 ■

Пример 2. Рассмотрим применение АД для графа, показанного на рис.1. Длины рёбер на-писаны на рисунке прямо около них. Составим вышеупомянутую таблицу 2. Она содержит все ответы, найденные аналогично примеру 1.

Кратчайшие пути из вершины 0 таковы:

в вершину 1: 0→1;

в вершину 5: 0→5;

в вершину 2: 0→1→2;

в вершину 3: 0→1→3;

в вершину 4: 0→1→4;

в вершину 7: 0→1→2→7;

в вершину 6: 0→5→6.

Длины путей находятся в столбцах «Последний помеченный». Слева стоят номера вершин в порядке получения постоянных меток; справа – длины кратчайших путей в эти вершины.

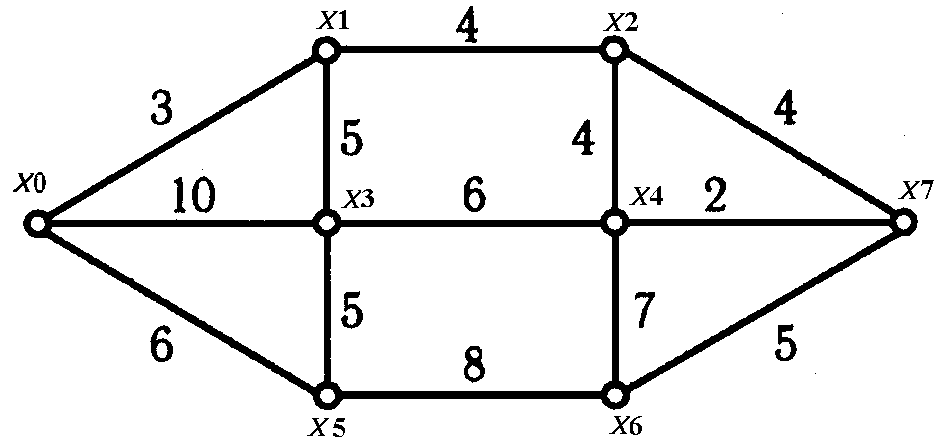
Рис.2

Таблица 2

Итера-ции

Посл помеч

Вершина 0

Вершина 1

Вершина 2

Вершина 3

Вершина 4

Вершина 5

Вершина 6

Вершина 7

№

c

P

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

■

Задание 1. Используя АД, найти кратчайшие пути между вершиной 0 и остальными вершинами в заданных графах. Длины рёбер написаны рядом с рёбрами.

■

Замечание. Рассмотренный алгоритм находит кратчайшие пути в неориентированном графе. Однако этот же самый алгоритм находит кратчайшие ориентированные пути в ориенти-рованном графе (см. все определения в разделе 6-3). Просто в описании алгоритма надо все упоминаемые там рёбра заменить на дуги. В частности, l (c, x) будет означать длину дуги (c, x), ведущей из вершины c в вершину x.

---

Дата добавления: 2015-10-16