I. Описание алгоритма реализации операции.

Задача курсового проекта заключается в разработке схемы арифметического устройства для вычисления S=A_max² – 1, работающего по алгоритму Бута.

Исходными данными являются:

количество разрядов массива – 3

количество разрядов числа – 8

количество разрядов знака – 1

Комбинационную схему реализовать в базисе 3ИЛИ-НЕ.

На основании исходных данных и предъявленных требований составим алгоритм работы устройства:

1. Установка счетчика на необходимое число тактов.
2. Выбор из массива с помощью компаратора максимального элемента.
3. Подача выбранного значения на регистры RGA и RGB.
4. Возведение в квадрат числа A_max (умножение числа A_max на само себя) с помощью алгоритма Бута.
5. Вычитание из результата 1.
6. Получение окончательного результата S.

Из построения схем умножения видно, что основную задержку процесса выработки результата обуславливает большое количество операций сложения. Уменьшение количества слагаемых позволяет сократить время суммирования. Это можно осуществить, используя модифицированный алгоритм Бута, позволяющий умножать сразу два разряда числа.

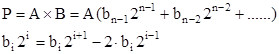
Это соотношение позволяет разреживать последовательность степеней суммы частичных произведений. Мы исключаем нечётные степени:

Рис 1.1–Схема разбиения двоичного числа по алгоритму Бута.

Исключение чётных и нечётных степеней позволяет сократить количество произведений вдвое, что увеличивает скорость операций.

Частичные произведения имеют следующий вид:

, где i-порядковый номер группы.

Так как число частичных произведений уменьшилось примерно вдвое, при применении этого алгоритма говорят об умножении сразу на два разряда.

Для возможных сочетаний b_i+1,b_i,b_i-1 можно составить таблицу частичных произведений. Данная таблица будет приведена далее при разработке дешифратора.

II. Блок-схема устройства и описание работы цикла.

Рассмотрим работу устройства по его блок-схеме.

Рис 2.1–Блок схема реализации устройства

По общей структуре схема представляет собой совокупность трех блоков: сравнения (выбор A_max), умножения по алгоритму Бута (возведения A_max в квадрат) и блока вычитания (реализация операции A_max² - 1).

В начале массив чисел в двоичном коде подается в блок сравнения, где с помощью компаратора CMP и регистра RG max выбирается максимальное число. Далее это число подается на два регистра сдвига RGA и RGB (регистры множителя и множимого).

Множимое (содержимое RGB) в прямом и дополнительном кодах подается на мультиплексор. Множитель сдвигается на два разряда и поступает на дешифратор, который анализирует тройки разрядов, декодирует их и даёт мультиплексору сигналы выбора того или иного варианта частичных произведений. Мультиплексор по поданному сигналу выбора передаёт на сумматор необходимый вариант частичной суммы. Окончательный результат получается суммированием частичных произведений с учётом их взаимного сдвига в разрядной сетке.

III. Временные диаграммы работы устройства .

Рассмотрим временные диаграммы работы устройства по блочно:

Для блока сравнения имеем:

Рис 3.1– Временные диаграммы управляющих импульсов.

Для блока сравнения будем иметь:

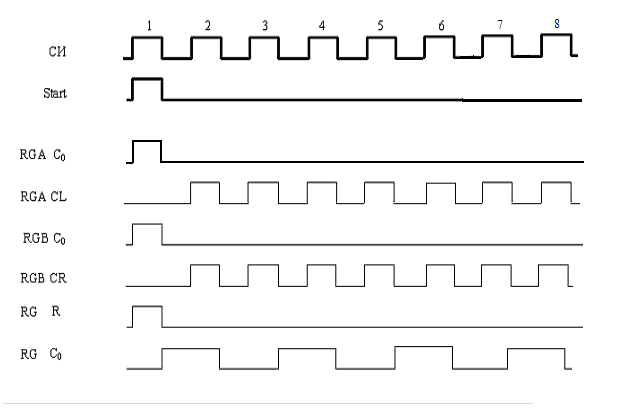
Рис 3.2– Временные диаграммы управляющих импульсов.

Непосредственные значения на выходах для каждого такта будут приведены ниже, когда будет рассматриваться конкретный пример. Это вызвано большой разрядностью чисел и соответственно количеством выходов, поэтому для лучшего понимания и наглядности в примере будем рассматривать сразу числовое значение для группы выходов конкретного элемента.
IV. Составление и минимизация комбинационных схем .

Дата добавления: 2015-10-16