Поиск максимального потока.

Пусть задана сеть S. Введём важное понятие разреза сети. Разрезом сети называется та-кое множество С дуг сети S, после удаления которых сеть распадается на несколько изолиро-ванных друг от друга частей, так что источник x ₁ и сток x_n оказываются в разных частях, при-чём ни одно подмножество С этим свойством не обладает.

Пример 4. В сети, показанной на рис.2, множество дуг { v ₄, v ₅, v ₆} образует разрез; разрез образуют также множества дуг { v ₆, v ₇, v ₈} и { v ₄, v ₅, v ₇, v ₉} (все эти разрезы показаны на рис.6). Множество дуг { v ₁, v ₅, v ₆, v ₈} разреза не образует (см. рис.7). Дуги, образующие указанные мно-жества, на рис.6 и 7 отмечены штриховкой ■

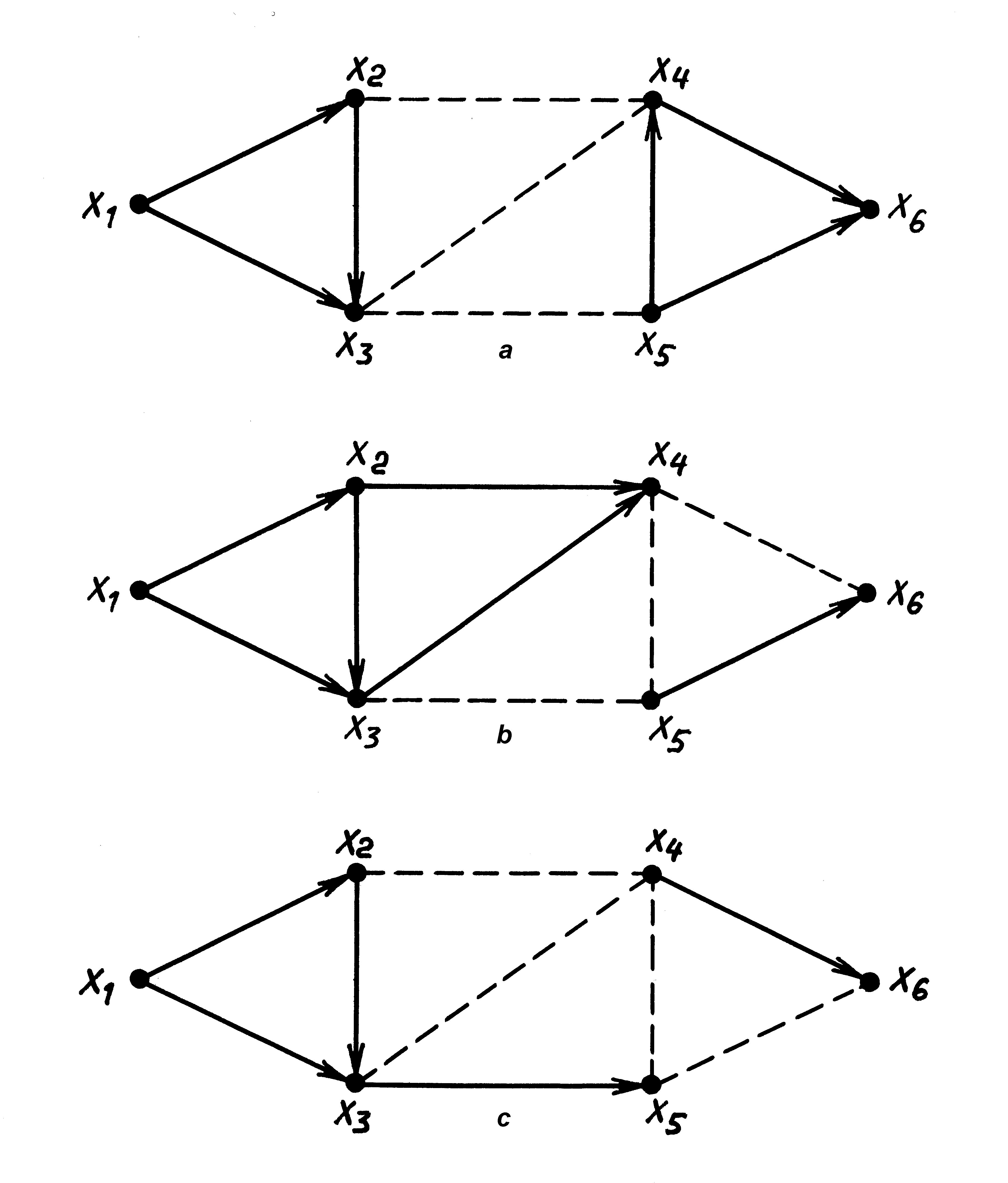Рис.6

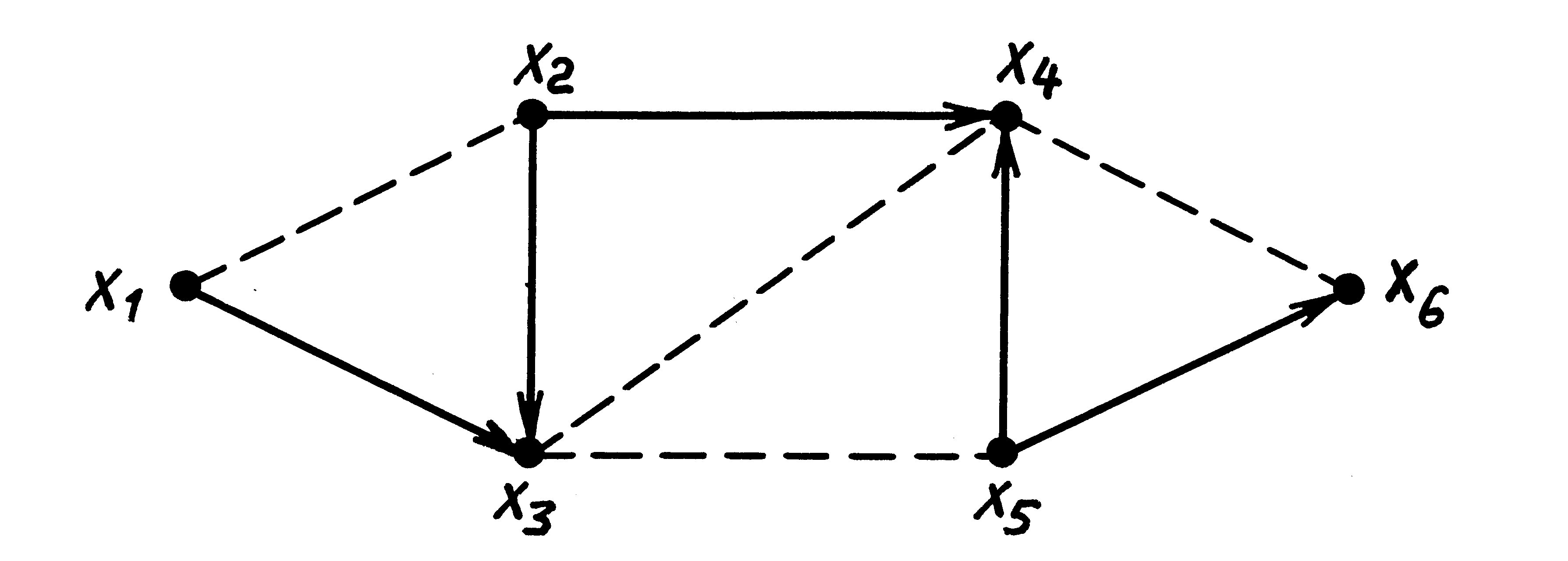Рис.7   Рис.8

Разрезы удобно изображать также линиями (не обязательно прямыми), «разрезающими» соответствующие дуги. На рис.8 показан разрез { v ₆, v ₇, v ₈}. Дуги относительно разреза «ведут себя» по-разному. Обозначим через А_s множество вершин, каждая из которых может быть сое-динена неориентированным путём с источником, через А_t - множество остальных вершин гра-фа, которые соединяются неориентированным путём со стоком.

Пример 4. Для разреза { v ₆, v ₇, v ₈}, показанного на рис.6 b и 8

А_s = { x ₁, x ₂, x ₃, x ₄}, А_t = { x ₅, x ₆};

для разреза { v ₄, v ₅, v ₆} (рис.6 а)

А_s = { x ₁, x ₂, x ₃}, А_t = { x ₄, x ₅, x ₆} ■

Легко понять, что каждая дуга разреза соединяет между собой вершины, лежащие в раз-ных множествах: одна в А_s, а другая в А_t. Дуга v называется прямой дугой разреза, если она выходит из А_s и входит в А_t; обратной, если она выходит из А_t и входит в А_s. В разрезе { v ₆, v ₇, v ₈} дуги v ₆ и v ₈ - прямые, а дуга v ₇ - обратная. Далее разрезы будем обозначать латинскими буквами A, B,....

Пусть u - поток в сети, Р (u) - величина этого потока. Потоком u (A) через разрез A назы-вается число, равное сумме потоков u_j во всех прямых дугах разреза A минус сумма потоков u_j во всех обратных дугах разреза A.

Утверждение 2. Для любого разреза A

u (A) = Р (u). (7)

Содержательно это утверждение понятно: все, что «вытекает» из источника, проходит по сети и «втекает» в сток. Это же количество продукта протекает через любой разрез. Поэтому надо сложить все, что течёт в нужном направлении (учтя с обратным знаком то, что течёт в противоположном направлении, т.е. по обратным дугам).

Пропускной способностью с (A) разреза A называется сумма пропускных способностей всех его прямых дуг. Ясно, что для любого разреза A и любого потока в сети u

u (A) ≤ с (A). (8) Действительно, сумма потоков в прямых дугах разреза не превосходит с (A); потоки же в об-

ратных дугах входят в u (A) со знаком минус, откуда сразу следует (8).

Разрез A, пропускная способность которого с (A) минимальна (минимум берется по всем разрезам сети S), называется минимальным разрезом. Из определений минимального разреза, максимального потока и формул (7) и (8) следует, что максимальный поток в сети не превосхо-дит пропускной способности минимального разреза. Гораздо более сложным является следую-щее утверждением

Утверждение 3. Максимальный поток равен пропускной способности минимального раз-реза ■

Алгоритм поиска потока в сети, для которого выполняется указанное в утверждении 3 ра-венство, излагается далее.

Пример 6. Найдем минимальные разрезы (и тем самым величины максимальных потоков) в нескольких простых сетях. В сети рис.1 минимальный разрез образует дуги v ₁ и v ₂, выходящие из источника x ₁. Его пропускная способность равна 4-ём. В сети рис.2 минимальным является разрез { v ₆, v ₇, v ₈}, показанный на рис.6 b и 8. Его пропускная способность равна 3. Обратим вни-мание, что дуга v ₇ (с пропускной способностью 5) здесь не учитывается, поскольку она является обратной дугой этого разреза. В сети рис.9 минимальный разрез указан линией. Его пропускная способность равна 3. В этом разрезе всего три дуги являются прямыми, остальные - обратны-ми.

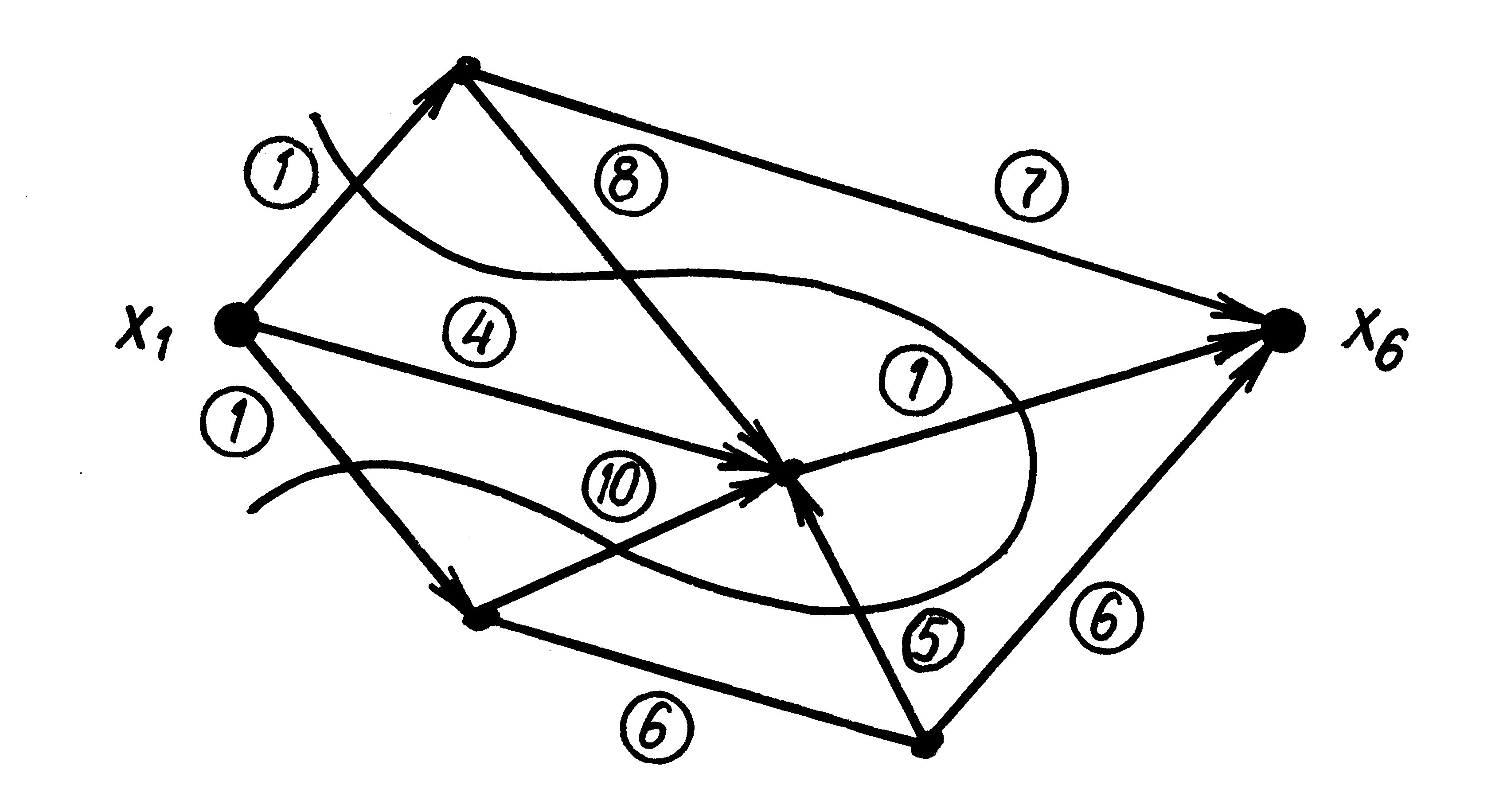
Рис.9 ■

4.1. Алгоритм Форда-Фалкерсона (АФФ). Перейдем к изложению алгоритма, предло-женному американскими математиками Фордом и Фалкерсоном в 1945г. (впервые опубликован в 1951г.). Он находит поток u с максимальной величиной Р (u), т.е. решает задачу (1) - (3). В основе этого алгоритма лежит переход от уже построенного потока u к новому потоку u', тако-му, что Р (u') > Р (u). Если такой переход оказывается невозможным, то это значит, что поток u является решением исходной задачи (т.е. поток u уже является максимальным).

Алгоритм перехода от потока u к новому потоку u' состоит из четырёх этапов:

1. Построение меток у вершин сети (исходя из заданного потока u).

2. Построение так называемого увеличивающего пути между источником и стоком (ис-ходя из построенных на этапе 1 пометок).

3. Вычисление инкремента найденного увеличивающего пути (исходя из самого пути и заданного потока u).

4. Построение нового потока u' (исходя из заданного потока u, построенного на этапе 2 увеличивающего пути и вычисленного на этапе 3 инкремента) ■

Наиболее важным и сложным этапом является этап 1. Рассмотрим его отдельно, учитывая, в частности, то обстоятельство, что расстановка пометок у вершин используется в самых разно-образных задачах, связанных с графами (см., например, раздел 6-4.1).

1. Алгоритм расстановки меток. В процессе работы этого алгоритма каждая вершина сети находится в одном из следующих трёх состояний:

1. Не помечена.

2. Помечена и не просмотрена.

3. Помечена и просмотрена.

Каждая вершина может перейти из состояния с мéньшим номером в состояние с бóльшим номером (не помеченная вершина может стать помеченной и не просмотренной; помеченная и не просмотренная вершина может стать помеченной и просмотренной). Обратные переходы, как и изменение полученных меток, невозможны. Как и во всех других алгоритмах, при отсутс-твии явного указания после проверки условия всегда выполняется следующий шаг.

0. Инициализация. Источник x ₁ получает метку 0; вершина x ₁ объявляется помеченной и не просмотренной; все остальные вершины объявляются не помеченными.

1. Из множества помеченных и не просмотренных вершин произвольно выбираем любую. Пусть это будет вершина x_i.

2. Помечаем индексом i все не помеченные ранее вершины x, обладающие следующим свойст-вом: существует дуга v_j, ведущая из х_i в x, для которой u_j < c_j (говорят, что дуга v_j не насыщена в прямом направлении). Вершина x объявляется помеченной и не просмотренной.

3. Если после выполнения шага 2 сток x_n оказывается помеченным, алгоритм 1 расстановки по-меток завершает работу и следует переход к описываемому далее алгоритму 2 построения уве-личивающего пути.

4. Помечаем индексом i все не помеченные ранее вершины x, обладающие следующим свойст-вом: существует дуга v_j, ведущая из x в х_i, для которой u_j > 0 (говорят, что дуга v_j не насыщена в обратном направлении). Вершина x объявляется помеченной и не просмотренной.

5. Вершина x_i объявляется помеченной и просмотренной.

6. Если текущее множество помеченных и не просмотренных вершин не пусто, то переходим к шагу 1.

7. АФФ завершает работу. Рассматриваемый в качестве исходного для алгоритма 1 расстановки меток поток u является искомым максимальным потоком ■

При реализации алгоритма целесообразно описывать сеть таблицей вида следующей таб-лицы 1. Таблица содержит n × n ячеек, каждая из которых состоит из двух клеток (напомним, что через n обозначено число вершин сети). Ячейка таблицы с номером (i, j), находящаяся на пере-сечении i -ой строки и j -ого столбца, делится на две клетки – левую и правую – и заполняется только в том случае, если в сети есть дуга, ведущая из вершины i в вершину j. Поскольку по определению потоковой сети из стока ни одна дуга не выходит, то последняя строка таблицы остаётся незаполненной. Поэтому она будет использоваться другим образом: в каждую её ячей-ку с номером j будет записываться текущее состояние вершины j (в левую клетку) и её метка (в правую клетку). Состояния вершин и метки определены при описании алгоритма. В основной части таблицы размера (n −1)× n в левую клетку ячейки (i, j) записывается поток по дуге (i, j), в правую – пропускная способность этой дуги. В отличие от состояний вершин, эти величины в процессе работы алгоритма расстановок меток не меняются.

Таблица 1. Общий вид таблицы для алгоритма расстановки меток

			• • •	j	• • •	n
				• • •
•••				• • •
i	• • •	• • •	• • •	u	c	• • •	• • •
•••				• • •
n –1				• • •
	σ 1	μ 1	• • •	• • •	σj	μj	• • •	σn	μn

Если j – номер вершины, выбираемой на шаге 1, то при выполнении шага 2 просматрива-ются все ячейки таблицы, находящиеся в j -ой строке. По построению таблицы, заполненным ячейкам соответствуют вершины, в которые ведёт дуга из вершины j. Для каждой из них дела-ются операции шага 2 алгоритма. Затем (если следует переход на шаг 4) на шаге 4 просматрива-ются все ячейки таблицы, находящиеся в j -ом столбце. Для заполненных ячеек делаются опера-ции шага 4 алгоритма. Заметим, что ячейки (j, j) в таблице 1 при j < n никогда не заполняются, поскольку дуг вида (j, j), т.е. петель при вершине, в потоковых сетях не бывает. Ячейка (n, n) в последней строке содержит информацию, относящуюся к самой вершине n.

После изменения состояний и меток вершин в соответствии с шагами 2 и 4 вновь выбира-ется одна из вершин с состоянием 2 (если таковая существует) и выполнение алгоритма про-должается. Важно, что после инициализации, т.е. начального заполнения таблицы, рисунком, изображающим сеть, можно не пользоваться: таблица содержит всю необходимую информа-цию.

Пример 7. Применим алгоритм 1 расстановки пометок для сети, показанной на рис.2 и для удобства дальнейшего изложения перерисованной здесь. В качестве исходного рассмотрим

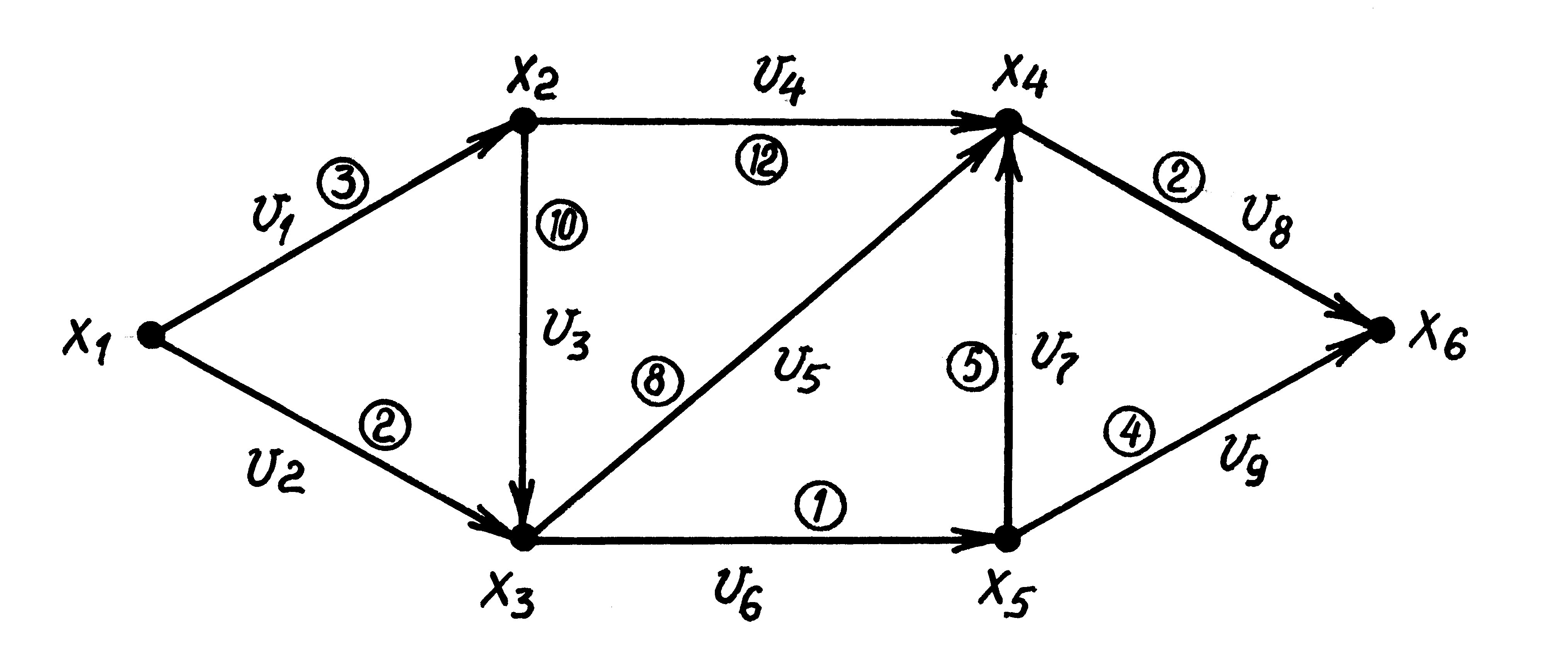
поток u = (2, 0, 1, 1, 1, 0, 0, 2, 0) (см. пример 2). При «ручной» реализации алгоритма воспользу-емся описанной непосредственно перед данным примером таблицей типа 1.

Таблица 2. Инициализация для расстановки пометок по заданному потоку

При инициализации таблицы 1, в соответствии с алгоритмом расстановки пометок, вер-шина 1 (источник) объявляется помеченной и не просмотренной (состояние 2), а все остальные вершины объявляются непомеченными (состояние 1). Метки при инициализации не определя-ются. В левую клетку ячейки (i, j) запишем поток по дуге (i, j), в правую – ограничение в ней. Таким образом, в таблице 1 представлен результат инициализации, и в этой таблице собрана вся необходимая для дальнейшего информация.

Итерация 1. Результаты итерации записываются в таблицу 2.1, которая сначала является просто копией таблицы 2. Выбирается любая помеченная и не просмотренная вершина в состо-янии 2. Таковая имеется только одна – вершина 1, поэтому она и выбирается. Далее, в соответс-твии с алгоритмом 1, рассматриваются все вершины, в которые ведут дуги из вершины 1. Этим вершинам соответствуют заполненные ячейки 1-ой строки: 2-ая и 3-ья. Поскольку в обеих ячей-ках число в левой клетке меньше числа в правой клетке, то это и значит, что обе дуги: v ₁ = (1, 2) и v ₂ = (1, 3) не насыщены в прямом направлении. Поэтому, в соответствии с алгоритмом, вер-шины 2 и 3 получают метку 1 и становятся отмеченными, но не просмотренными, т.е. перехо-дят из состояния 1 в состояние 2, что и отмечается в таблице 2.1. Далее, в соответствии с шагом 4 алгоритма, надо проверить вершины, из которых ведут дуги в вершину 1. Но поскольку за-полненных ячеек в 1-ом столбце таблицы 2.1 нет, то, значит, нет и таких вершин, и все опера-ции шага 4 просто не выполняются. Для завершения итерации осталось, в соответствии с шагом 5, перевести вершину 1 из состояния 2 в состояние 3 и отметить это в таблице 2.1.

Таблица 2.1. Итерация 1 расстановки пометок по заданному потоку

Итерация 2. Результаты итерации записываются в таблицу 2.2, которая сначала является просто копией таблицы 2.1. Выбирается любая помеченная и не просмотренная вершина (т.е. в состоянии 2). Таковых имеется две – вершины 2 и 3. Поскольку можно выбирать любую, для определённости здесь и далее будем выбирать вершину с минимальным номером. Таковой яв-ляется вершина 2. Далее, в соответствии с алгоритмом 1, рассматриваются все вершины, в кото-рые ведут дуги из вершины 2. Этим вершинам соответствуют заполненные ячейки 2-ой строки: 3-ья и 4-ая. Вершина 3 уже помечена (находится в состоянии 2) и, в соответствии с описанием шага 2, здесь не рассматривается. Вершина 4 ещё не помечена (находится в состоянии 1) и по-ток (1) в дуге (2, 4) меньше ограничения (12). Поэтому, в соответствии с шагом 2, вершина 4 по-лучает метку 2 и переходит в состояние 2 (она объявляется помеченной и не просмотренной). Далее, в соответствии с шагом 4 алгоритма, надо проверить вершины, из которых ведут дуги в вершину 2. Таковой является только вершина 1, которой соответствует единственная заполнен-ная клетка во 2-ом столбце. Но поскольку вершина 1 помечена, то операции шага 4 просто не выполняются. Для завершения итерации осталось, в соответствии с шагом 5, перевести верши-ну 2 из состояния 2 в состояние 3 и отметить это в таблице 2.2.

Таблица 2.2. Итерация 2 расстановки пометок по заданному потоку

Итерация 3. Результаты итерации записываются в таблицу 2.3, которая сначала является просто копией таблицы 2.2. Выбирается любая помеченная и не просмотренная вершина в со-стоянии 2. Таковых имеется две – вершины 3 и 4. Выберем вершину 3 (как имеющую мéньший номер). Далее, в соответствии с алгоритмом 1, рассматриваются все вершины, в которые ведут дуги из вершины 3. Этим вершинам соответствуют заполненные ячейки 3-ьей строки: 4-ая и 5-ая. Вершина 4 уже помечена (находится в состоянии 2) и, в соответствии с описанием шага 2, здесь не рассматривается. Вершина 5 ещё не помечена (находится в состоянии 1) и поток (0) в дуге (3, 5) меньше ограничения (1). Поэтому, в соответствии с шагом 2, вершина 5 получает метку 3 и переходит в состояние 2 (она объявляется помеченной и не просмотренной). Далее, в соответствии с шагом 4 алгоритма, надо проверить вершины, из которых ведут дуги в вершину 3. Таковыми являются вершины 1 и 2, которым соответствуют заполненные ячейки в 3-ем стол-бце. Но поскольку вершины 1 и 2 помечены, то операции шага 4 просто не выполняются. Для завершения итерации осталось, в соответствии с шагом 5, перевести вершину 3 из состояния 2 в состояние 3 и отметить это в таблице 2.3.

Таблица 2.3. Итерация 3 расстановки пометок по заданному потоку

Итерация 4. Результаты итерации записываются в таблицу 2.4, которая сначала является просто копией таблицы 2.3. Выбирается любая помеченная и не просмотренная вершина в со-стоянии 2. Таковых имеется две – вершины 4 и 5. Выберем вершину 4 (как имеющую мéньший номер). Далее, в соответствии с алгоритмом 1, рассматриваются все вершины, в которые ведут дуги из вершины 4. Этим вершинам соответствуют заполненные ячейки 4-ьей строки. Таковой является только 6-ая ячейка. Вершина 6 ещё не помечена (находится в состоянии 1), но поток (2) в дуге (4, 6) равен ограничению (2) в этой дуге. Поэтому, в соответствии с шагом 2 алгоритма, никаких меток не ставится. Далее, в соответствии с шагом 4 алгоритма, надо прове-рить вершины, из которых ведут дуги в вершину 4. Таковыми являются вершины 2, 3 и 5, кото-рым соответствуют заполненные ячейки в 4-ем столбце. Но поскольку все эти вершины уже по-мечены, то операции шага 4 просто не выполняются. Для завершения итерации осталось, в со-ответствии с шагом 5, перевести вершину 4 из состояния 2 в состояние 3 и отметить это в таб-лице 2.4.

Таблица 2.4. Итерация 4 расстановки пометок по заданному потоку

Итерация 5. Результаты итерации записываются в таблицу 2.5, которая сначала является просто копией таблицы 2.5. Выбирается любая помеченная и не просмотренная вершина в со-стоянии 2. Таковой является единственная вершина 5. Далее, в соответствии с алгоритмом 1, рассматриваются все вершины, в которые ведут дуги из вершины 5. Этим вершинам соответст-вуют заполненные ячейки 5-ой строки. Таковыми является 4-ая и 6-ая ячейка. Вершина 4 уже помечена, так что она не рассматривается. Вершина 6 ещё не помечена (находится в состоянии 1), и поток (0) в дуге (5, 6) меньше ограничения (4) в этой дуге. Поэтому, в соответствии с ша-гом 2 алгоритма, вершина 6 получает метку 5 и объявляется помеченной и не просмотренной, т.е. переходит в состояние 2, что и отмечается в таблице 2.5. Далее, в соответствии с шагом 3, алгоритм прекращает работу, поскольку сток – вершина 6 – теперь помечен.

Таблица 2.5. Итерация 5 расстановки пометок по заданному потоку

Задание 2. Применить алгоритм расстановки меток ко всем потокам из задания 1 (см. при-мер 7) ■

Рассмотрим теперь алгоритмы 2 - 4 по отдельности.

2. Алгоритм построения увеличивающего пути. Алгоритм 2 начинает работу, когда сток сети помечен.

1. Концом пути p является сток n.

2. Пусть уже построен путь от некоторой вершины x до стока n. Пусть i - метка у вершины x. Тогда предыдущей вершиной пути p является вершина i.

3. Если вершина i является источником, то искомый путь p построен; переходим к алгоритму 3 вычисления инкремента пути p. В противном случае возвращаемся на шаг 2 ■

Пример 8. Применим алгоритм 2 построения увеличивающего пути для сети с метками, представленными в таблице 2.5. В соответствии с алгоритмом 2 путь p заканчивается в стоке 6. Поскольку у вершины 6 стоит метка 5, предыдущей вершиной пути p является вершина 5. Предшествующей 5 вершиной является вершина 3, предшествующей 2 – источник 1. Поэтому сам увеличивающий путь от источника к стоку оказывается таким: 1→3→5 →6 ■

Задание 3. Построить увеличивающие пути для меток, найденных в задании 2 ■

Пусть дуга (x_i, x_j) входит в некоторый путь p (не обязательно от источника к стоку). Дуга (x_i, x_j) называется прямой дугой пути p, если вершина x_i расположена на пути p ближе к его на-чалу, чем вершина x_j, и называется обратной дугой пути p, в противном случае. Заметим, что одна и та же дуга может быть прямой в одном пути и обратной в другом. Путь p от источника к стоку, во всех прямых дугах которого поток u_j < c_j, а во всех обратных дугах поток u_j > 0, называется увеличивающим путём.

Утверждение 4. Путь p от источника к стоку, построенный алгоритмом 2 по меткам, пост-роенным алгоритмом 1, является увеличивающим путём ■

3. Алгоритм вычисления инкремента увеличивающего пути. Пусть путь p = z ₁→ z ₂→...→ z_k является увеличивающим путём.

1. Положим D = , i = 0.

2. i = i + 1.

3. Положим

D_i =

4. Положим D = min{ D, D_i }.

5. Если i < k -1, возвращаемся к шагу 2; в противном случае алгоритм 3 прекращает работу ■

Найденное значение D является той «добавкой», на которую могут быть увеличены потоки во всех дугах пути p (именно поэтому он назван «увеличивающим»).

Пример 9. Вычислим инкремент увеличивающего пути p = x ₁→ x ₃ → x ₅→ x ₆, найденного в примере 8 (см. последнюю строку таблицы 2.5). Положим D = = 12.

Далее:

i = 1, v_j = (x ₁, x ₃), c_j = 2, u_j = 0, D ₁ = c_j - u_j = 2, D = min(D, D ₁) = 2;

i = 2, v_j = (x ₃, x ₅), c_j = 1, u_j = 0, D ₂ = c_j - u_j = 1, D = min(D, D ₂) = 1;

i = 3, v_j = (x ₅, x ₆), c_j = 4, u_j = 0, D ₃ = c_j - u_j = 4, D = min(D, D ₃) = 1.

Таким образом, инкремент увеличивающего пути p = x ₁→ x ₃→ x ₅→ x ₆ равен 1. Это значит, что потоки во всех дугах данного пути могут быть увеличены на 1 ■

Задание 4. Найти инкременты увеличивающих путей, найденных в задании 3 ■

4. Алгоритм построения нового потока u'. Новый поток u' определяется по заданному потоку u, построенному увеличивающему пути p и вычисленному инкременту D этого пути следующей формулой:

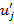= (j = 1, 2,..., m). (9)

Пример 10. Найдём новый поток u' для сети, рассмотренной в примерах 7 - 9. Все три дуги в пути p = x ₁→ x ₃→ x ₅→ x ₆ являются прямыми. «Старые» потоки по этим дугам были равны 0, а новые равны 1. Учитывая нумерацию дуг в данной сети (см. рис.2), получаем u' = (2, 1, 1, 1, 1, 1, 0, 2, 1).

Задание 5. Найти новые потоки по потокам из задания 1 и инкрементам, найденным в за-дании 4 ■

---

Дата добавления: 2015-10-16