Алгоритм Флойда-Уоршолла

В этом разделе рассматривается другой способ решения задачи о кратчайших путях для всех пар вершин ориентированного графа. В отличие от алгоритма Дейкстры, в АФУ допуска-ются дуги с отрицательной длиной. Однако циклы с отрицательной длиной запрещаются; точн-ее, предполагается, что такие циклы в рассматриваемом графе G = á X, V ñ отсутствуют. Если же циклы отрицательной длины присутствуют, то этот факт выясняется уже в процессе выполнения алгоритма

АФУ основан на представлении пути, ведущего из вершины a в вершину b и проходяще-го через промежуточную вершину c как последовательность двух путей: из a в c и из c в b. По-нятно, что если этот путь является кратчайшим среди всех путей того же вида (т.е. ведущих из a в b через c), то указанные части также должны быть кратчайшими. В алгоритме особую роль играют промежуточные вершины с максимальным номером (в некоторой заданной нумерации вершин). Промежуточной вершиной простого пути р = á v ₁, v ₂,..., v_l ñ будем называть любую из вершин v ₂,..., v_{l −1}.

Будем считать, что вершины графа G = á X, V ñ занумерованы числами от 1 до n. Длина дуги с началом в вершине i и концом в вершине j обозначена через l (i, j) (как и в других ситуациях, l (i, j) = 0, если i = j,и l (i, j) = ∞, если дуги(i, j)в графе нет). Рассмотрим произвольное k ≤ n. Для данной пары вершин i, j Î V рассмотрим все пути из i в j, у которых все промежуточные вершины принадлежат множеству {1, 2, …, k }. Пусть p − путь минимальной длины среди всех таких путей. Он является простым путём, поскольку предполагается, что в графе нет циклов отрицательной длины. Как найти длину этого пути, зная длины всех таких (кратчайших) путей для всех пар вершин при мéньших k?

Для пути p есть две возможности.

Если k не входит в р, все промежуточные вершины пути p содержатся в множестве {1, 2, …, k −1}. Тогда путь р является кратчайшим путём из i в j, промежуточные вершины которого принадлежат множеству{1, 2, …, k −1}.

Если k является промежуточной вершиной пути р, она разбивает его на два участка р ₁ и р ₂ (вершина k встречается лишь однажды, гак как р − простой путь). Поэтому путь р ₁ будет кратчайшим путём из i в k, путь р ₂будет кратчайшим путём из k в j, а промежуточными вершинами на обоих путях будут вершины из множества {1, 2, …, k −1}. Эти рассуждения лежат в основе излагаемого ниже алгоритма.

Алгоритм Флойда-Уоршолла (АФУ). Алгоритм находит кратчайшие пути для всех пар вершин заданного ориентированного графа G. Для реализации алгоритма вводятся четыре квадратные матрицы размера n ´ n, где n – число вершин в заданном графе G:

Матрица D = (d_ij) текущих кратчайших расстояний;

Вспомогательная матрица H = (h_ij) для пересчёта текущих кратчайших расстояний;

Матрица предшествия Π = (π_ij) (матрица предпоследних вершин на текущих кратчайших путях из i в j);

Вспомогательная матрица Ψ = (ψ_ij) для пересчёта предпоследних вершин.

В процессе работы алгоритма происходит заполнение матриц и изменение их элементов. Алго-ритм прекращает работу после n- го шага.

Шаг 0 (Инициализация). Положить

d_ij = l (i, j) (i, j = 1, …, n);

π_ij = .

Шаг k (1≤ k ≤ n).

1. Для всех i, j = 1, …, n выполнить следующие операции:

1.1. Положить

z = d_ik + d_kj, (2)

1.2. Если z < d_ij, то положить h_ij = z и ψ_ij = π_kj. В противном случае положить h_ij = d_ij и ψ_ij = π_ij. Заметим, что из d_ik = ∞ следует, что z = ∞ и неравенство z < d_ij не выполняется.

2. Для всех i, j = 1, …, n положить d_ij = h_ij, π_ij = ψ_ij.

Шаг F. На этом шаге определяются кратчайшие пути для всех пар вершин. Кратчайший путь из начальной вершины i в любую другую вершину j строится следующим образом: верши-ной, предшествующей j на искомом пути, является вершина p = π_ij; вершиной, предшест-вующей p на искомом пути, является вершина q = π_ip, и т.д., вплоть до начальной вершины i. Искомый путь из i в j состоит из тех же вершин в обратном порядке ■

При «ручной» реализации АФУ будет удобно результаты каждой итерации записывать в последовательные таблицы специального вида – по одной на каждую итерацию. Реализация АФУ состоит в последовательном заполнении таблиц и переносе части результатов в следую-щую таблицу. Эта схема подробно описана при нахождении всех кратчайших путей в конкрет-ном графе, рассмотренном в следующем примере.

Пример 3. Проиллюстрируем работу АФУ на примере графа, показанного на рис.3. На этом рисунке рядом с вершинами показаны их номера; более крупным шрифтом рядом с дуга-ми показаны их длины.

Рис. 3. Ориентированный граф с 5-ью вершинами и 9-ью дугами

Все операции алгоритма являются операциями над данными, записанными в таблицу типа таблицы 3. В эту таблицу входит 5×5 ячеек, каждая из которых состоит из трёх клеток. Эти клетки будут называться левой, средней и правой. Кроме этих 25 ячеек, таблица содержит ле-вый столбец, состоящий из 5-и клеток, и верхнюю строку, состоящую из 5 ячеек, содержащих по 2 клетки каждая (левую и правую). Их роль будет указана ниже.

Таблица 3. Исходная таблица для АФУ

№

Инициализация. Она состоит в заполнении таблицы 4.1а, совпадающей с таблицей 3. По-следовательно рассматриваются все дуги исходного графа, показанного на рис.3. Если дуга ве-дёт из вершины i в вершину j, то в среднюю клетку ячейки с индексом (i, j) (т.е. находящуюся на пересечении i -ой строки и j -го столбца) вставляется длина дуги из вершины i в вершину j, а в правую клетку – номер i. После этого во всех ячейках с совпадающими индексами (i, i) в среднюю клетку записывается 0. Наконец, во всех остальных ячейках в средние клетки напи-шем знак ∞. Больше ничего в таблицу 4.1а не записывается. Все упомянутые данные берутся непосредственно из рис.3. В дальнейших конструкциях рисунок не участвует.

Таблица 4. Результат инициализации

№

∞

−4

∞

∞

∞

∞

∞

∞

−5

∞

∞

∞

∞

Итерация 1. k = 1. На итерации 1 происходит последовательное преобразование данных, полученных при инициализации и представленных в таблице 4. Сначала заполняются левый столбец и верхняя строка. В i -ую клетку левого столбца копируется содержимое из средней клетки ячейки с индексом (i, k) (номер k равен номеру итерации, и в данном случае k = 1). В j -ую ячейку верхней строки копируется содержимое средней и правой клеток ячейки с индексом (k, j) (k = 1). Результат этой операции приведён в таблице 4.1a. Заметим, что при копировании пустой клетки её копия также будет пустой клеткой.

Таблица 4.1a. Заполнение левого столбца и верхней строки

№

∞

−4

∞

−4

∞

∞

∞

∞

∞

∞

∞

∞

−5

∞

∞

∞

∞

∞

Следующей операцией является заполнение левых клеток каждой из 25 ячеек. Правило заполнения достаточно простое. В ячейку с индексом (i, j) вставляется сумма чисел из i -ой клетки левого столбца и левой половины j -ой клетки верхней строки. Операция соответствует пункту 1.1 общего шага АФУ. Заметим, что для любого x (в том числе x = ∞) x + ∞ = ∞ + x = ∞. Результаты данной операции представлены в следующей таблице 4.1b.

Таблица 4.1b. Заполнение сумм

№

∞

−4

∞

∞

−4

−4

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

−5

∞

−2

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

Следующая операция – изменение (в некоторых случаях) записей в средних и правых клетках всех ячеек. Правило также очень простое:

1. Если число в левой клетке меньше числа в средней клетке, то

1.1. Число из левой клетке записывается в среднюю клетку.

1.2. В правую клетку записывается номер из правой клетки верхней строки, находя-щейся в одном столбце с рассматриваемой ячейкой.

2. В противном случае ничего не делается.

В качестве примера рассмотрим ячейку (4,2) в которой число в левой клетке (5) меньше числа в средней клетке (∞). Тогда число 5 надо записать в среднюю клетку вместо ∞, а в правую клетку надо записать номер 1. Легко понять, что описанная операция (выделение минимумов и копи-рование значений) в точности представляет собой операции пунктов 1.2 и 2 общего шага АФУ. Результаты её выполнения записаны в таблице 4.1c. Заметим, что числа в средних клетках ячейки (i, j) – это длины построенных на рассматриваемой итерации и ранее путей из вершины i в вершину j, а номера в правых клетках – это предпоследние вершины на этих путях.

Таблица 4.1c. Заполнение минимумов и предпоследних вершин

№

∞

−4

∞

∞

−4

−4

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

−5

∞

−2

−2

∞

∞

∞

∞

∞

∞

∞

∞

∞

Для завершения итерации 1 осталось сделать следующее. Числа из левых клеток всех яче-ек удаляются. Удаляются также все данные из левого столбца и верхней строки. В результате получаем таблицу 4.1d, которая по форме совпадает с таблицей 4, полученной в результате инициализации.

Таблица 4.1d. Результат итерации 1

№

∞

−4

∞

∞

∞

∞

∞

−5

−2

∞

∞

∞

Итерация 2. k = 2. На итерации 2 происходит последовательное преобразование данных, полученных на итерации 1 и представленных в таблице 4.1d. Естественно, что алгоритм не ме-няется, поэтому подробных объяснений к каждой таблице, как на итерации 1, не даётся. Выпол-нение итерации 2 демонстрируется в таблицах 4.2a – 4.2d, аналогичных таблицам 4.1a – 4.1d. Заметим, что в левый столбец копируются данные из 2-го столбца, а в верхнюю строку – из 2-ой строки таблицы 4.2а, так как k = 2.

Таблица 4.2а. Заполнение левого столбца и верхней строки

№

∞

∞

∞

−4

∞

∞

∞

∞

∞

−5

−2

∞

∞

∞

∞

Таблица 4.2b. Заполнение сумм

№

∞

∞

∞

∞

∞

−4

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

−5

−2

∞

∞

∞

∞

∞

∞

∞

∞

∞

Таблица 4.2c. Заполнение минимумов и предпоследних вершин

№

∞

∞

∞

∞

−4

∞

∞

∞

∞

∞

∞

∞

∞

∞

−5

−2

∞

∞

∞

∞

∞

∞

∞

∞

∞

Таблица 4.2d. Результат итерации 2

№

−4

∞

∞

∞

−5

−2

∞

∞

∞

Итерация 3. k = 3. На итерации 3 происходит последовательное преобразование данных, полученных на итерации 2 и представленных в таблице 4.2d. Выполнение итерации 3 демонст-рируется в таблицах 4.3a – 4.3d.

Таблица 4.3а. Заполнение левого столбца и верхней строки

№

∞

−4

∞

∞

∞

∞

−5

−5

−2

∞

∞

∞

∞

Таблица 4.3b. Заполнение сумм

№

∞

∞

−4

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

−5

∞

−1

−5

−5

−2

∞

∞

∞

∞

∞

∞

∞

∞

∞

Таблица 4.3c. Заполнение минимумов и предпоследних вершин

№

∞

∞

−4

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

−5

∞

−1

−1

−5

−5

−2

∞

∞

∞

∞

∞

∞

∞

∞

∞

Таблица 4.3d. Результат итерации 3

№

−4

∞

∞

∞

−1

−5

−2

∞

∞

∞

Итерация 4. k = 4. На итерации 4 преобразование данных показано с мéньшей детализаци-ей. Требуемые операции выполняются так же, как и ранее, но промежуточные результаты не за-писываются в новые таблицы, а последовательно записываются в одни и те же ячейки и клетки. Результаты приводятся в таблице 4.4.

Таблица 4.4. Результат итерации 4

№

−1

−4

−4

−1

−1

−5

−2

Итерация 5. k = 5. Эта итерация является последней перед финальным шагом F. В таблице 4.5 содержатся кратчайшие расстояния для всех пар вершин и вершины, предпоследние на каж-дом таком пути.

Таблица 4.5. Результат итерации 5

№

−3

−4

−4

−1

−1

−5

−2

Шаг F. Найдём сами кратчайшие пути, используя правые клетки в ячейках. Напомним, что число в правой клетке в ячейке (i, j) – это номер вершины, предшествующей на кратчайшем пути из i в j вершине j, т.е. номер предпоследней вершины на этом пути.

Для пути из 1 в 2 такой вершиной является вершина 3 (см. таблицу 4.5); далее, для пути из 1 в 3 такой вершиной является вершина 4; для пути из 1 в 4 такой вершиной является вершина 5; наконец, для пути из 1 в 5 такой вершиной является вершина 1. Таким образом, кратчайший путь из вершины 1 в вершину 2 таков: 1→5→4→3→2. По построению, все промежуточные пу-ти: 1→5→4→3; 1→5→4; 1→5 также являются не только кратчайшими путями, но и именно те-ми кратчайшими путями, которые найдены данным алгоритмом. Все кратчайшие пути из вер-шины 1 уже найдены. Они таковы: 1→5→4→3→2; 1→5→4→3; 1→5→4; 1→5.

Далее, рассмотрим пути из вершины 2 в другие вершины. На пути из 2 в 1 предпоследней вершиной является вершина 4, а непосредственно перед ней – начальная вершина 2, и весь путь таков: 2→4→1. Далее, на пути из 2 в 3 предпоследней вершиной является 4, и путь таков: 2→4 →3. Путь из 2 в 4 состоит из одной дуги 2→4. Наконец, на пути из 2 в 5 предпоследней верши-ной является 1, а путь из 2 в 1 уже известен, поэтому имеем кратчайший путь 2→4→1→5. Все кратчайшие пути из вершины 2 таковы: 2→4→1; 2→4→3; 2→4; 2→4→1→5.

Кратчайшие пути из вершины 3 таковы: 3→5→4→1; 3→2; 3→5→4; 3→5.

Кратчайшие пути из вершины 4 таковы: 4→1; 4→3→2; 4→3; 4→1→5.

Кратчайшие пути из вершины 5 таковы: 5→4→1; 5→4→3→2; 5→4→3; 5→4 ■

3.1. Циклы отрицательной длины. В АФУ предполагалось, что в заданном графе отсутс-твуют циклы отрицательной длины. При обосновании АФУ это требование существенно, так как само разбиение пути, проходящего через вершину k, на два пути, не содержащих k в качест-ве промежуточной вершины, возможно только при единственном вхождении k в путь, что, в свою очередь, гарантируется как раз отсутствием циклов отрицательной длины. Поскольку в достаточно сложных случаях сам факт наличия или отсутствия таких циклов не является оче-видным, необходим специальный алгоритм, устанавливающий этот факт. Более того, в некоторых практически важных задачах (см. главу 9) требуется найти цикл отрицательной длины или установить их отсутствие безотносительно к нахождению кратчайших путей.

Оказывается, что решение этой проблемы является «побочным продуктом» АФУ. Подроб-нее. Применяем АФУ к произвольному графу, не выясняя заранее, содержит ли он циклы отрицательной длины. Для этого после каждого шага, начиная с 1-го (k =1), проверяем все числа на диагонали матрицы D (напомним, что после инициализации все они равны 0). Пусть хотя бы один элемент (скажем, d_ii) оказывается меньше 0. Тогда путь с концом в вершине i, найден-ный так же, как и приведённый сразу после описания АФУ способ нахождения кратчайшего пути в вершину i, окажется циклом с началом и концом в вершине i, длина которого равна от-рицательному числу d_ii. Это следует просто из описания алгоритма, который на каждом k- о м шаге находит текущие кратчайшие пути для всех пар вершин (включая пары с совпадающими

вершинами)

Пример 4. Проиллюстрируем работу АФУ на примере графа, показанного на рис. 4. В нём есть цикл 3→1→2→3 отрицательной длины −1. В соответствии с описанием «руч-ной» версии АФУ в примере 3, в результате инициализации получим таблицу 5. Далее, на итерации 1 из таблицы 5 получаем преобразо-ванную таблицу 5.1 точно так же, как это дела-лось в примере 3, а затем точно так же полу-чаем таблицы 5.2 и 5.3. После выполнения итерации 3 обнаружи-ваем путь из вершины 1 в ту же самую верши-ну 1, на котором предпоследней вершиной яв-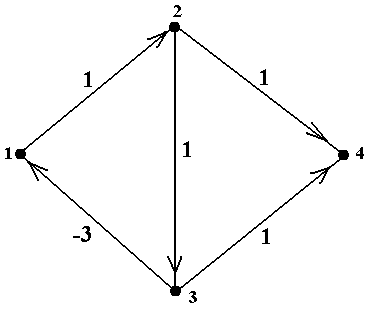

Рис. 4. Граф с отрицательным циклом

ляется вершина 3, перед ней – вершина 2, а перед вершиной 2 – опять вершина 1. Таким обра-зом, найден цикл 1→2→3→1; длина этого цикла, указанная в средней клетке ячейки (1, 1), рав-на −1, т.е. найден цикл отрицательной длины. Разумеется, одновременно найдены циклы 2→3

→1→2 и 3→1→2→3, отличающиеся от цикла 1→2→3→1 только начальной вершиной; их

длина также равна −1.

Таблица 5. Результаты инициализации

№

∞

∞

∞

−3

∞

∞

∞

∞

Таблица 5.1. Результат итерации 1

№

∞

∞

∞

−3

−2

∞

∞

∞

Таблица 5.2. Результат итерации 2

№

∞

−3

−2

−1

−1

∞

∞

∞

Таблица 5.3. Результат итерации 3

№

−1

−2

−1

−4

−3

−2

−2

∞

∞

∞

■

Таким образом, АФУ позволяет не только установить факт наличия или отсутствия цик-лов отрицательной длины, но и найти по крайней мере один из них.

Задание 2. Используя АФУ, в заданном ориентированном графе найтикратчайшие пути между всеми парами вершин, если циклы отрицательной длины не существуют, или найти такой цикл. Для образца см. примеры 3 и 4.

01 02

03 04

05 06

07 08

09 10

11 12

13 14

15 16

17 18

19 20

■

Замечание. Рассмотренный алгоритм находит кратчайшие пути и циклы отрицательной длины в ориентированном графе. Однако этот же самый алгоритм находит соответствующие пути и циклы в неориентированном графе (см. все определения в разделе 6-3). Просто в описа-нии алгоритма надо все упоминаемые там дуги заменить рёбрами. Например, l (c, x) обозначает длину ребра (c, x) с концами c и x.

Дата добавления: 2015-10-16