Решение задач нелинейного программирования в среде приложения Matlab

Метод покоординатного спуска (Гаусса – Зейделя)

На каждом шаге метод «приближается» к решению последовательно по каждой из координат. Переход от точки к точке +1 назовем «внешней» итерацией. Внутри каждой «внешней» итерации находятся n «внутренних» для последовательного вычисления координат точки +1.

.

,

,

,

…………………………………………………………,

.

,

.

Блок-схема алгоритма метода покоординатного спуска с постоянным

шагом и программа приведены в Приложении 1. Графическая

иллюстрация решения приведена на Рис.3.9.

Рисунок 3.9 – Графическая иллюстрация движения к максимуму методом

покоординатного спуска.

Градиентный метод с постоянным шагом.

На каждой итерации метод «приближается» к решению, вычисляя новое значение каждой координаты в соответствии с формулой. Блок-схема алгоритма метода с постоянным шагом и программа приведены в Приложении. Графическая иллюстрация решения приведена на Рис. 3.10.

Рисунок 3.10 – Движение к максимуму с постоянным шагом.

В примере Рис.3.11 происходит дробление шага на первой итерации

алгоритма. В этом можно убедиться, поставив точку останова на строке 56.

Рисунок 3.11 – Графическая иллюстрация метода с дроблением шага

Градиентный метод наискорейшего спуска.

На каждой итерации вычисляется значение шага γ, максимизирующее значение целевой функции:

.

Новые координаты вычисляются с помощью этого значения:

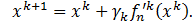
Скалярное произведение векторов-градиентов на двух смежных итерациях равно нулю:

Это означает, что движение от точки к точке происходит по взаимно-ортогональным направлениям. (Рис.3.12).

Рис.3.12 – Движение к экстремуму по взаимно-ортогональным направлениям в методе наискорейшего спуска.

Сравнение методов.

Для сравнения точности и быстродействия методов в данной работе используется следующий простой прием. В вышеприведенных примерах решалась простейшая задача, точное решение которой находится из системы линейных уравнений.

f(

В таблице 3.1 для каждого метода приводится число итераций к, за которое из одной и той же начальной точки алгоритм приходит в точку хк, норма вектора-градиента в которой становится меньше заданного числа δ =0,01 -точности метода. Точка хк является решением задачи. Методы сравниваются по значению отклонения этой точки от точки х*=0 – точного безусловного максимума.

Таблица 3.1 – Сравнения точности и быстродействия методов

Метод	Отклонение	Число итераций
Покоординатный спуск	0.0030555
«По всем координатам сразу» с постоянным шагом	0.0035189
«По всем координатам сразу» с дроблением шага	0.0040109
Метод наискорейшего спуска	0.0013446

ВЫВОДЫ

В данном дипломном проекте я представила решение задач нелинейного программирования различными методами для проведения анализа поведения этих методов на выбранных математических моделях нелинейного программирования.

Для достижения поставленной цели были выполнены следующие действия

-решены выбранные задачи нелинейного программирования графическим методом;

-решены выбранные задачи нелинейного программирования методом множителей Лагранжа

-представлена компьютерная реализация выбранных задач нелинейного программирования в среде пакетов Excel и Matlab

Дата добавления: 2015-10-21