Метод половинного деления

Естественным и наиболее распространенным на практике методом поиска экстремума функции одной переменной является метод последовательного деления отрезка пополам. Этот метод был известен еще в древней Греции как метод дихотомии.

Пусть требуется определить экстремум унимодальной функции Q (u) на отрезке с точностью . Отрезок делится пополам и вычисляются значения функции Q (x 1) = F 1 и Q (x 2) = F 2 в точках

x _{1,2= .}

На основе анализа значений и вдвое уменьшается интервал неопределенности и процесс повторяется пока . Блок-схема этого метода приведена на рис. 2.5, б.

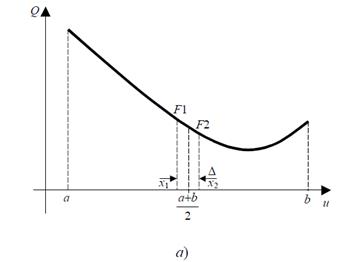
Рисунок 2.5 – Метод деления отрезка пополам:

а – геометрическая интерпретация; б – блок-схема

2.2.3 Метод "золотого сечения"

Гораздо эффективнее, с точки зрения уменьшения затрат на вычисления, метод "золотого сечения": интервал неопределенности делится не пополам, как в методе дихотомии, а в определенном иррациональном соотношении

Это соотношение выполняется при ...

Метод заключается в том, что по заданным a и b как можно точнее определяется значение внутренней точки x 1 (см. рис. 2.6, б) по формуле

x 1 = b – (b – a) / 1,618033989…

Рисунок 2.6 – Метод "золотого сечения":

а – золотое сечение; б – геометрическое представление

Точка x 2 определяется как точка,симметричная точке x 1 на отрезке (a - b).

На основе анализа значений F 1 = Q (x 1) и F 2 = Q (x 2) интервал неопределенности сокращается путем отбрасывания из рассмотрения отрезка в котором экстремум исключен, исходя из условий уни-модальности Q (u). Далее мы определим симметричную точку внутри новых границ, вычисляем значение Q в этой точке, проводим анализ и т.д. до тех пор, пока разность между симметричными точками внутри интервала неопределенности больше . Блок-схема алгоритма метода "золотого сечения" представлена на рис. 2.7.

Рисунок 2.7 – Блок-схема метода "золотого сечения"

Дата добавления: 2015-10-21