Экономическая трактовка метода множителей Лагранжа

В некоторых задачах множители Лагранжа допускают и экономическое толкование. Если толковать целевую функцию Q (u 1,..., un) как прибыль, получаемую некоторым предприятием при использовании ресурсов, а условия k ограничения на дефицит ресурсов, то при (u 1,..., un) < 0 прибыль, то максимум целевой функции будет расти.

Экономист такую задачу будет решать следующим образом. Он назначит некоторые цены на единицы ресурсов и предложит потребителю купить их по этой цене. Последний, максимизируя чистую прибыль , найдет (u 1,..., un) и скажет, сколько ресурсов он хотел бы купить. В экономике почти всегда бывает так, что чем больше 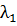, тем меньше 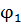(u 1,..., un), и чем меньше 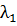, тем больше 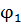(u 1,..., un). Если окажется, что 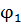(u 1,..., un) > 0, то экономист повысит цену, если 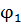(u 1,..., un) < 0 – понизит. Так будет происходить до тех пор, пока при некоторой цене, называемой равновесной, потребителю будет выгодно, чтобы дефицит ресурсов 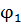(u 1,..., un) был равен нулю, при этом чистая прибыль будет максимальна, т.е. будут выполняться условия

Таким образом, равновесная цена с точностью до знака равна множителю Лагранжа.

\

Дата добавления: 2015-10-21