Метод Фибоначчи

Метод, использующий числа Фибоначчи, позволяет наиболее эффективно достичь заданной точности в поиске экстремума функции Q (u). Числа Фибоначчи определяются соотношением

F 0 = F 1 = 1; Fk = Fk –1 + Fk –2; k = 2, 3, …

При большом " k " отношение соседних чисел Фибоначчи близко к отношению "золотого сечения".

Этот метод делит интервал неопределенности не в постоянном соотношении, а в переменном и предполагает некоторое, вполне определенное, зависящее от , число вычислений значений функции Q (u).

По заданному определяется количество вычислений n и соответствующее ему число Фибоначчи Fn, исходя из соотношения

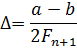
В остальном схема метода близка к методу "золотого сечения" в котором значение x 1 и x 2 (см. рис. 2.8) определяются отношением соответствующих чисел Фибоначчи.

Рис. 2.8– Блок-схема метода Фибоначчи

Дата добавления: 2015-10-21