Особые случаи. В заключение следует отметить особые случаи, когда градиент функции равен нулю и

В заключение следует отметить особые случаи, когда градиент функции равен нулю и когда градиент φ₁(u1,..., un) равен нулю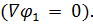

В первом случае решение может достигаться в точке экстремума функции множители 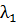равны нулю, и задача сводится к задаче безусловного экстремума и условия роли не играют. Во втором случае подозрительные на экстремум точки находятся из уравнений , в которых затем вычисляется значение критерия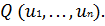

Для того, чтобы условия экстремума были справедливы и в особых случаях, функцию Лагранжа записывают в виде

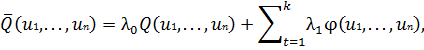
тогда можно утверждать, что для условного экстремума Q (u 1,..., un) необходимо существование таких чисел , , 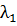одновременно не равных нулю, что в точке предполагаемого решения выполнены условия ≥ 0

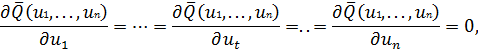
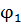(u 1,..., un) =0.

Если ≠ 0, то его можно выбрать положительным числом, обычно полагают = 1, это никак не отражается на решении.

Требуется найти минимум функц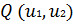ии = при условии .

Для решения записывается функция Лагранжа

,

для которой уже необходимо определить безусловный экстремум. Необходимое условие экстремума даст следующую систему уравнений:

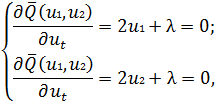
откуда 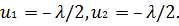Используя уравнение связи , получают и соответственно

.

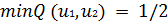По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве u 1 изделий первым способом затраты равны (4 u 1 + ), а при изготовлении u 2 изделий вторым способом они составляют (8 u 2+ 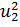). Определить, сколько изделий каждым из способов следует изготовить, так чтобы общие затраты на производство продукции были минимальными.

Математическая постановка задачи состоит в определении минимального значения функции при условиях .

Задача может быть решена методом множителей Лагранжа. Для этого без учета требования неотрицательности переменных составляется функция Лагранжа

Необходимое условие экстремума функции Лагранжа дает

откуда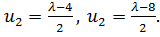

Подстановка найденных значений в условие u 1 + u 2 = 180 дает

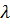− и, следовательно, 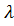=186 и, соответственно, u 1 = 91,

u 2 = 89.

По вторым частным производным можно показать, что найденная точка доставляет минимум функции Q (u 1, u 2), т.е. если будет изготовлено 91 изделие первым технологическим способом и 89 изделий вторым технологическим способом, общие затраты будут минимальны и составят Q min = 17 278.

Дата добавления: 2015-10-21