Геометрическая интерпретация метода множителей Лагранжа

Интерес представляют геометрический смысл множителей Лагранжа. Для такой интерпретации лучше рассмотреть задачу с двумя неизвестными и одним ограничением.

Пусть требуется найти минимум функции 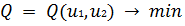при условии 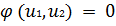. Если минимум существует, то в пространстве функция Q должна иметь вид воронки, а условие связи – это некоторая поверхность.

На рис. 4, б изображены на плоскости переменных u 1, u 2 линии уровня функции Q (u 1, u 2) и ограничение φ (u 1, u 2) = 0, представляющее собой линию. Составляется вспомогательная функция Q (u 1, u 2) = Q (u 1, u 2) + λφ (u 1, u 2). Необходимое условие экстремума дает:

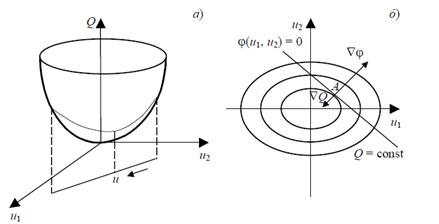
Рисунок 1.4 – Геометрический смысл множителей Лагранжа:

а – пространственное изображение;

б – изображение проекции на плоскость u 2 – u 1

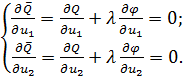или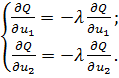

В точке А – точке касания линии 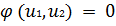с линией равного уровня функци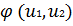и и 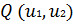имеют общую касательную и необходимое условие минимума представляет собой условие пропорциональности двух векторов: вектора 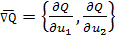– градиента функции 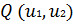и вектора 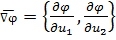– градиента функции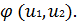

Два вектора пропорциональны друг другу лишь в том случае, если они коллинеарные. Так как градиент функции перпендикулярен касательной к линии уровня, то в точке А выполняется условие, и множитель 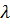является коэффициентом пропорциональности между векторам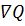и и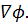

Дата добавления: 2015-10-21