Основные положения. Пусть требуется найти экстремум функции, например, минимум

Пусть требуется найти экстремум функции, например, минимум

Q(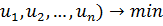, при условии

,

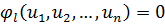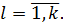
Согласно методу Лагранжа для решения задач на условный экстремум функции составляется вспомогательная функция Лагранжа, которая определяется соотношением

,

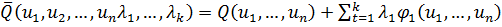где 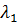, 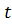= 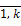– неопределенные множители Лагранжа.

Таким образом, задача нахождения условного экстремума функции сводится к задаче нахождения безусловного экстремума функции, но число неизвестных в ней n + k (u ι, ι = 1, n; λ j, j = 1, k).

Как известно из п. 1.2 необходимым условием безусловного экстремума функции является равенство нулю частных производных, которые для данного конкретного случая записываются в виде

.

и дает n уравнений для определения неизвестных. Эта система уравнений дополняется к уравнениям и, следовательно, получается (n + k) неизвестных и (n + k) уравнений.

Метод множителей Лагранжа дает лишь необходимые условия существования условного экстремума для непрерывных функций, имеющих также непрерывные производные, поэтому найденные значения переменных могут и не давать экстремума функции Q (u 1,..., un), их надо проверить с использованием достаточных условий экстремума функции многих переменных.

В окончательном решении задачи фактически множители Лагранжа не известны, поэтому задача совместного решения системы, иногда ставится как задача исключения " k " неизвестных переменных u ι с последующим решением остающейся системы n уравнений с n неизвестными.

Задача Лагранжа имеет " n – k " степеней свободы.

Дата добавления: 2015-10-21