|
Читайте также: |
Исследуемая функция может иметь несколько экстремумов. Если для всех значений независимых переменных выполняется условие
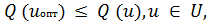то экстремум в точке u опт называется глобальным, другие экстремумы называются локальными.
Поскольку заранее число экстремумов функции Q (u) неизвестно, то для нахождения глобального экстремума необходимо, вообще говоря, найти и проверить все без исключения локальные экстремумы, имеющиеся у целевой функции решаемой задачи. С этой целью осуществляется поиск из различных начальных точек, для чего область изменения независимых переменных ui покрывается сеткой и начальная точка ui 0 выбирается из областей, полученных в результате проведенного сканирования.
Также для поиска глобального экстремума используют случайный поиск, в частности, методы Мон-те-Карло. Здесь экстремум находится с какой-то вероятностью.
В заключение следует отметить, что большое разнообразие методов нелинейного программирования свидетельствует, прежде всего, о сложности проблемы поиска и трудностях в оценке эффективности использования того или иного метода при решении конкретной задачи. Следует сопоставлять практическую эффективность вычислительных возможностей разных методов.
Методы нелинейного программирования служат не только для решения специфических задач, но являются также необходимым средством, к которому обращаются при решении оптимальных задач, а также задач вычислительной математики.
По мере развития математического моделирования роль этих методов будет несомненно вырастать, что приведет к более глубокой разработке существующих и созданию новых алгоритмов поиска экстремума в задачах нелинейного программирования.
Дата добавления: 2015-10-21; просмотров: 194 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод проектирования вектора-градиента | | | Графический метод решения задач нелинейного программирования |