Читайте также:
|
При рассмотрении реальных задач оптимизации на переменные состояния накладываются условия типа равенств или неравенств, которые задают область изменения независимых переменных.
Задача нелинейного программирования в этом случае формулируется следующим образом: требуется найти оптимум (минимум) функции Q(
) при 
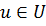и условия, что 
.
Число условий типа неравенств может быть любым, т.е. меньше или больше числа независимых переменных. Если при решении такой задачи экстремум целевой функции будет находится внутри допустимой области изменения независимых переменных 
, ограниченной неравенствами 
, то в некоторых случаях эту задачу можно решить рассмотренными выше методами поиска без учета ограничений. Вести поиск подобным образом при наличии условий типа равенств обычно невозможно. Если же экстремум целевой функции будет расположен на границе допустимой области, то для его отыскания применяют специальные методы.
Дата добавления: 2015-10-21; просмотров: 72 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод квантования симплексов | | | Метод проектирования вектора-градиента |