Решение задач нелинейного программирования в среде приложения Excel

Рассмотрим примеры нелинейной оптимизационной экономической задачи, её экономико-математическую модель и метод компьютерной реализации в среде пакета Excel.

Особенности компьютерной реализации

Задача (модель) нелинейного программирования формулируется так же, как и общая задача оптимального программирования со следующими требованиями к целевой функции и допустимой области:

целевой функции f(,..., 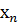) и (или) одна из функций (,..., 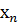) являются нелинейными:

min(max) f (,..., ),

(,..., ) { .

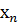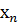У произвольной задачи нелинейного программирования некоторые или все свойства, характерные для задач линейного программирования, отсутствуют. Вследствие этого задачи нелинейного программирования несравнимо сложнее задач линейного программирования, и для них не существует общего универсального метода их решения (аналогично симплексному методу).

Есть целый ряд методов решения задач нелинейного программирования. В пакете Excel реализован метод множителей Лагранжа, идея которого заключается в преобразовании задачи условной оптимизации в задачу безусловной оптимизации, решение которой производится методами поиска - градиентными методами (методы первого порядка) или методами Ньютона (методы второго порядка). Наиболее распространенными являются градиентные методы.

Необходимо помнить, что существующие методы дают возможность находить только локальные оптимумы (помимо случаев, когда задачи обладают соответствующими свойствами выпуклости и вогнутости). Если же есть подозрение, что в допустимой области целевой функции может иметь несколько оптимумов, то эту область следует разбить на ряд областей и в каждой из них определить свои локальные оптимумы, а затем из всех локальных оптимумов выбрать глобальный. В таком практическом подходе задача поиска глобального оптимума сводится к решению ряда задач, в которых ищется свой (локальный) оптимум.

Следует отметить, что в подавляющем большинстве практических задач оптимизации существует только один оптимум.

Решение задачи нелинейного программирования (реализация модели нелинейной оптимизации) средствами Excel отличается от решения линейного программирования следующим:

- назначаются начальные значения искомых переменных так, чтобы ЦФ в начальной точке не была равна нулю,

- в диалоговом окне Поиск решения в режиме Параметры не надо вводить Линейная модель.

В Excel признаком достижения оптимума является величина относительного приращения целевой функции на каждой итерации . Оптимум считается достигнутым, если выполняется услови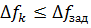е , где точность, назначаемая при решении задачи (Параметры).

Примером задачи нелинейного программирования является модель оптимального формирования портфеля ценных бумаг (модель Марковица минимального риска).

В этой модели приняты следующие обозначения:

, - доля капитала, потраченная на покупку ценных бумагу j-го вида (весь выделенный капитал принимается за 1);

— средняя ожидаемая доходность j-й ценной бумаги, (mj называют эффективностью j-й ценной бумаги);

- дисперсия случайной доходности j-й ценной бумаги, (называют риском j-й ценной бумаги).

В предположении о некоррелированности ценных бумаг (их независимости) модель Марковица имеет вид:

Найти ,j=1,…,n, минимизирующие риск портфеля ценных бумаг

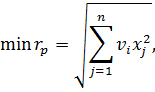
при условии, что обеспечивается заданное значение эффективности портфеля mp, т.е.

.

Нелинейной является целевой функции.

Задачи оптимизации, в результате решения которых искомые значения переменных должны быть целыми числами, называются задачами (моделями) целочисленного (дискретного) программирования:

min(max) f (,..., )

(,..., ) {

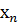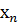Если множество индексов ={1,2,...,n}, то задачу называют полностью целочисленной, если , то - частично целочисленной.

Рассмотрим задачу оптимального формирования портфеля ценных бумаг. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (4, 10), (10, 40), (40, 80). Нижняя граница доходности портфеля задана равной 15.

Построим экономико-математическая модель

Введем необходимые обозначения, пусть х_j (j =1, 2, 3) - число предметов

j -го типа, которое следует погрузить на баржу. Тогда математическая модель задачи о подборе для баржи допустимого груза максимальной ценности запишется следующим образом:

4 x ₁ + 10 x ₂ + 40 х ₃ ≥ 15

x ₁ + x ₂ + x ₃ = 1

x_j ≥ 0, j = 1, 2, 3.

Заполняем рабочий лист данными.

Рисунок 3.4 – Рабочий лист программы

Рабочий лист может быть подготовлен в виде, представленном на рис.3.5, формулы этого листа приведены в ячейках.

Рисунок 3.5 – Рабочий лист

Диалоговое окно, отвечающее приведенному выше рабочему листу, представлено на рис.3.6.

Рис. 3.6 – Диалоговое окно

Реализуя приведенную модель средствами пакета Excel (рис. 2.9), будем иметь оптимальный портфель Марковица:

x ₁ = 0,5213, х ₂ = 0,2078, х ₃ = 0,2709,

т.е. доли ценных бумаг оказались равными 52,13 %; 20,78 % и 27,09 %. При этом минимальный риск - 23,79, доходность портфеля оказалась равной заданной - 15.

Рисунок 3.7 – Результаты решения

Проиллюстрируем результаты с помощью Мастера диаграмм

Рисунок 3.8 – Графическая иллюстрация результатов

Дата добавления: 2015-10-21