Электрические фильтры 4 страница

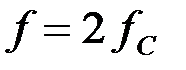Сопротивление на частоте тоже будет иметь индуктивный характер:

Рис.3.5.4,б

Зависимость характеристического сопротивления показана на рис.3.5.4,б Коэффициент затухания «» на частоте будет определяться следующим образом:

А на частоте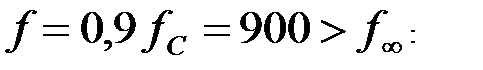

Задача 3.5.5 Определить полосу пропускания фильтра низкой частоты типа «m», представленного на рис.3.5.5, а, прототипом которого, является фильтр типа «k», если m =0,4; Вычислить значения сопротивлений звеньев фильтра типа «m» на частоте 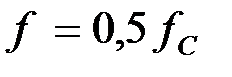. Найти коэффициент фазы «β» на частоте 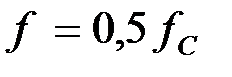и коэффициент затухания «α» на частоте

Рис.3.5.5,а

Решение Данный фильтр типа «m» является последовательно – производным от Т – образного фильтра низкой частоты типа «k». Последовательно производное звено фильтра типа «m» состоит из двух последовательно соединенных элементов: эквивалентной индуктивности равной:

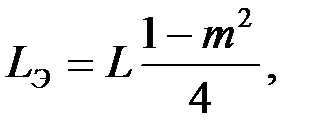и эквивалентной емкости

Схема фильтра приведена на рис. 3.5.3,б.

Рис.3.5.3,б

Полосы пропускания фильтров типа «k» и типа «m» совпадают, следовательно частоту среза найдем как: Определим значения сопротивлений звеньев фильтра типа «m» на частоте :

Характеристическое сопротивление фильтра типа «k» совпадает с характеристическим сопротивлением последовательно-производного фильтра типа «m» . Для определения характеристического сопротивления фильтра–прототипа на частоте воспользуемся выражением:

Характеристическое сопротивление производного фильтра типа «m» на частоте найдем как [8]:

Из расчетов 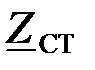и следует, что характеристические сопротивления прототипа и фильтра типа «m» совпадают.

Найдем частоту бесконечного затухания: 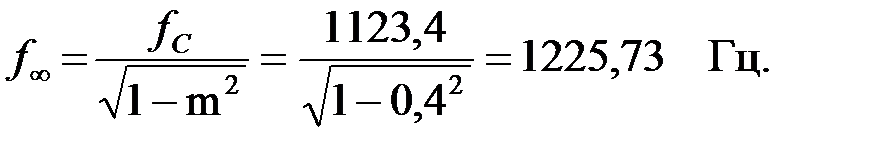Т.к. частота то коэффициент затухания можно определить, используя соотношение [8]:

тогда

Коэффициент фазы в полосе пропускания на частоте найдем как:

Задача 3.5.6 Последовательно-производный фильтр низкой частоты типа «m», собранный по Т – образной схеме имеет частоту среза параметр m =0,506, номинальное волновое характеристическое сопротивление k =420 Ом. Определить параметры элементов фильтра и значение характеристического сопротивления на частотах: Построить зависимости коэффициента затухания «α» и коэффициента фазы «β» от частоты.

Рис.3.5.6,а

Решение Последовательно-производный Т – образный фильтр, показан на рис.3.5.6. Т.к. частоты среза прототипа и производного фильтра типа «m» совпадают, то индуктивность и емкость прототипа ФНЧ типа «k» найдем следующим образом:

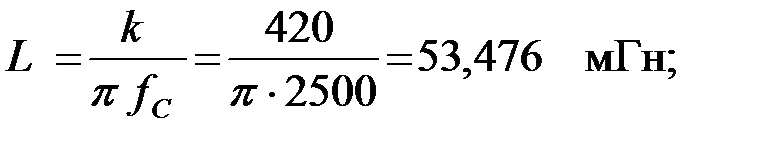
Зная параметр «m» определим индуктивности и емкости фильтра типа «m» (рис.3.5.6,а):

Известно, что характеристические сопротивления прототипа и фильтра типа «m» совпадают. Проверим это положение на разных частотах.

1. Пусть тогда

2. Пусть тогда

Коэффициент затухания в диапазоне от частоты среза до частоты бесконечного затухания 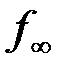можно найти следующим образом [8]:

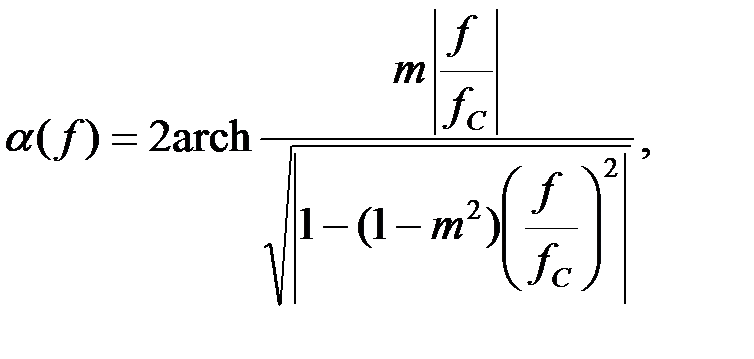где

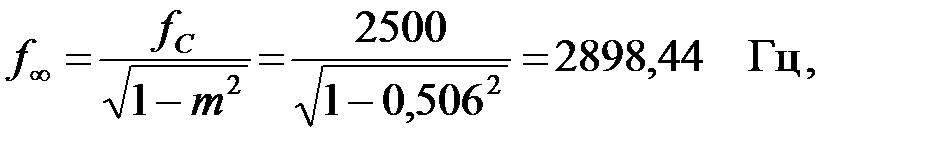
При частотах сигналов коэффициент затухания определяется иначе:

Рис.3.5.6,б	Коэффициент фазы в полосе пропускания можно найти из выражения:
Рис.3.5.6,в	а в полосе затухания: Графики изменения коэффициентов затухания «α» и фазы «β» от частоты показаны на рис.3.5.6,б и рис.3.5.6,в.

Задача 3.5.7 Определить полосу пропускания параллельно- производного фильтра низкой частоты типа «m», представленного на рис.3.5.7, прототипом которого, является П – образный фильтр типа «k», если m =0,5, Вычислить параметры элементов фильтра типа «m» и характеристическое сопротивление на Найти коэффициент затухания на частоте

Рис.3.5.7

Решение Полосы пропускания фильтров типа «k» и типа «m» совпадают, поэтому частоту среза найдем как:

Номинальное волновое характеристическое сопротивление:

Зная «m», определим параметры элементов фильтра типа «m»:

Определив параметры элементов, найдем сопротивления звеньев фильтра на частоте

Известно, что характеристические сопротивления прототипа и фильтра типа «m» совпадают. Проверим это положение для заданной частоты

Найдем частоту бесконечного затухания:

Т.к, заданная то коэффициент затухания можно определить из соотношения [8]:

тогда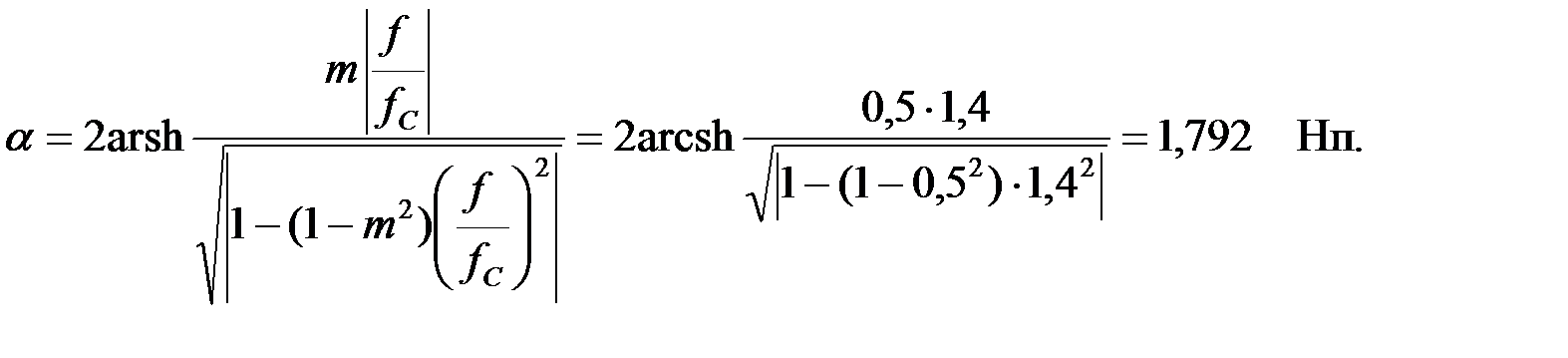

Задача 3.5.8 Определить параметры последовательно-производного Т – образного фильтра высокой частоты типа «m», представленного на рис.3.5.8,а прототипом которого, является фильтр типа «k», если номинальное волновое характеристическое сопротивление =80 Ом, а коэффициент m = 0,7. Рассчитать характеристическое сопротивление фильтра на частотах 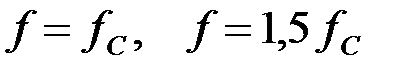а также коэффициент затухания на частоте 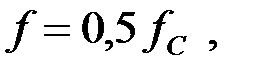если . Построить зависимости коэффициента затухания «α» и коэффициента фазы «β» от частоты.

. Рис.3.5.8,а

Решение Частоты среза прототипа и фильтра типа «m» совпадают. Поэтому индуктивность и емкость элементов прототипа ФВЧ найдем как:

Используя параметры элеменов фильтра типа «k», определим параметры элементов производного фильтра типа «m»:

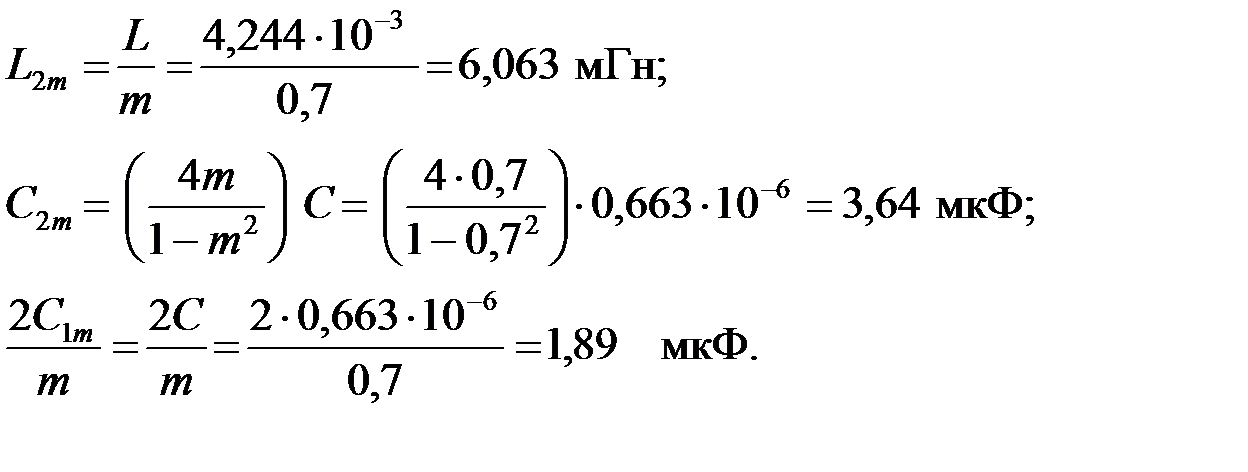
Зная параметры звеньев производного фильтра вычисляем сопротивления 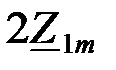и на частоте среза:

Известно, что характеристические сопротивления прототипа и фильтра типа «m» совпадают, проверим данное наложение на разных частотах.

На частоте среза:

На частоте :

Найдем сопротивления звеньев производного Т – образного фильтра и :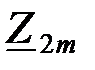

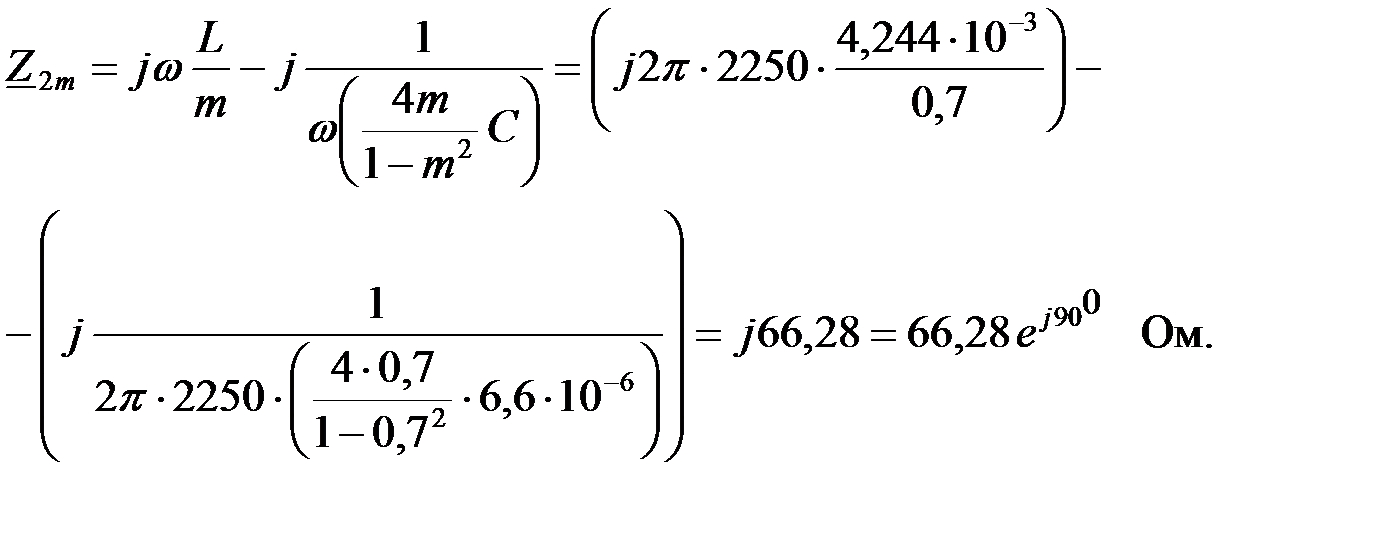
Рассчитаем характеристические сопротивления прототипа и производного фильтров на частоте

Тоже самое рассчитаем на частоте :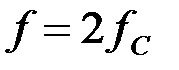

Для определения коэффициента затухания, вычислим частоту бесконечного затухания:

Тогда коэффициент затухания на частоте будет равен:

Зависимости и показаны на рис.3.5.8,б. и рис.3.5.8,в.

Дата добавления: 2015-10-21