Решение. Запишем уравнения активного четырехполюсника, используя режим короткого замыкания

Запишем уравнения активного четырехполюсника, используя режим короткого замыкания зажимов «pq»:

Рис.2.4.2,а

Определим коэффициенты для пассивного ЧП, представленного на рис.2.4.2,б, для чего найдем сопротивления холостого хода и короткого замыкания при прямом и обратном питании ЧП:

Рис.2.4.2,б

Тогда коэффициенты ЧП найдем, используя известные соотношения:

Используя уравнение связи проверим правильность определения коэффициентов

определим из режима одновременного короткого замыкания зажимов «mn» и «pq» (рис.2.4.2,в).

Здесь ветвь с источником ЭДС замкнута накоротко, поэтому ток, протекающий через данный источник, определим по закону Ома:

Рис.2.4.2,в

Сопротивления при коротком замыкании зажимов «mn» и «pq», будут включены параллельно, поэтому ток, протекающий через второй источник ЭДС найдем как:

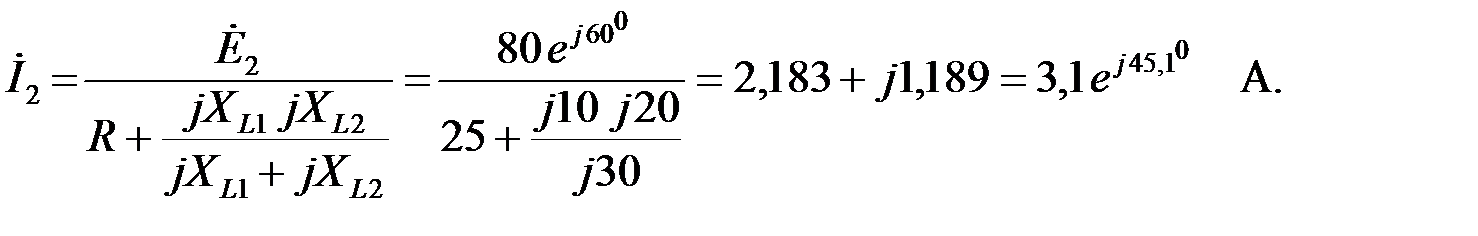
Ток, протекающий через реактивное сопротивление равен току короткого замыкания , который может определить методом «чужой ветви»:

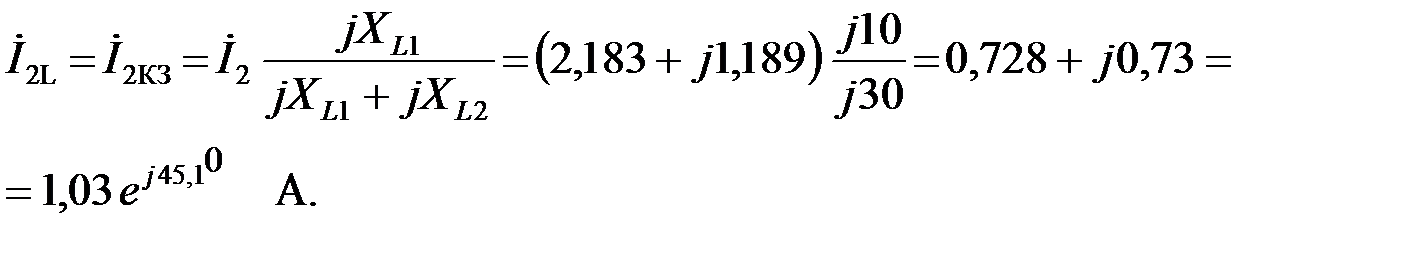
Подобным способом найдем ток, протекающий через реактивное сопротивление :

Ток короткого замыкания найдем используя первый закон Кирхгофа:

Используя полученные соотеношения запишем уравнения активного ЧП в А – форме:

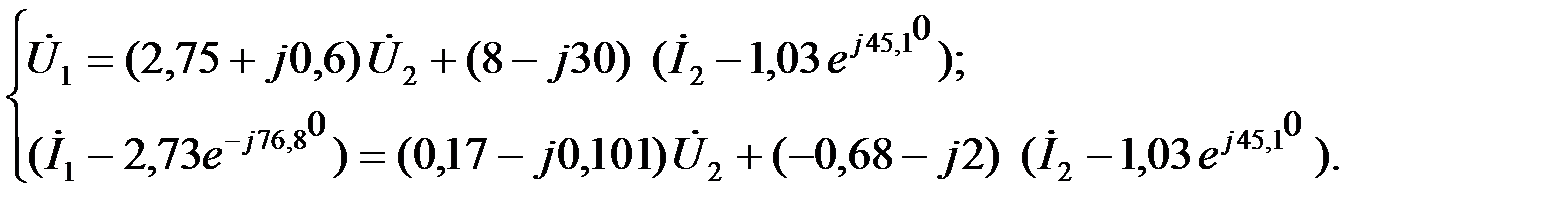
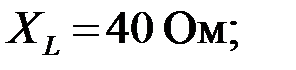
Задача 2.4.3 Для активного ЧП, представленного на рис.2.4.3,а, заданы следующие параметры: Найти Z – параметры и записать уравнения ЧП для нахождения 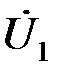и в Z – форме.

Дата добавления: 2015-10-21