
Читайте также:
|
Зная уравнения двух каскадно-соединенных ЧП, найдем уравнение для ЧП, полученного при таком соединении:
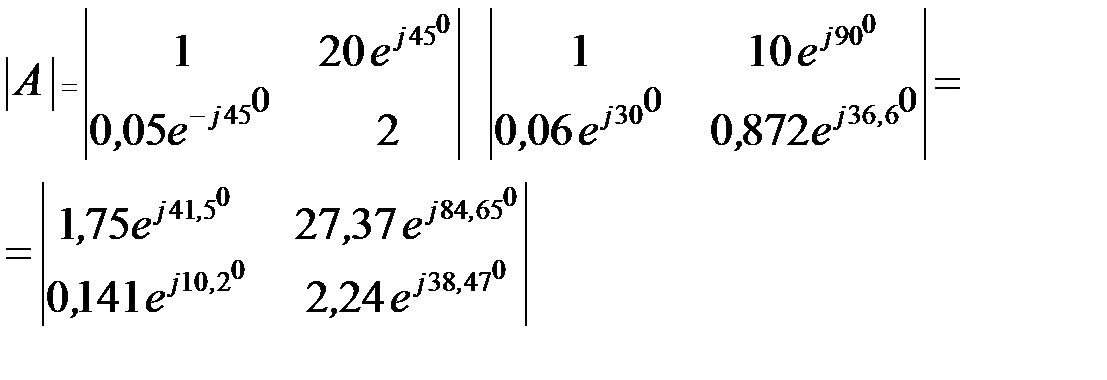
Рис.2.3.2
Проверяем правильность определения коэффициентов ЧП, используя уравнение их связи:

Для того, чтобы найти ток на выходе каскадно-соединенных четырехполюсников, найдем характеристическое сопротивление  :
:

Зная  и
и  , найдем ток
, найдем ток  на выходе составного ЧП:
на выходе составного ЧП:

Используя А – форму записи уравнений четырехполюсников, определим напряжение и ток на входе составного ЧП:

Таким образом, приборы включенные на входе и выходе составного ЧП показали: 
Задача 2.3.3 Два одинаковых симметричных ЧП, схема одного из которых показана на рис.2.3.3 с параметрами  соединены разными способами: а) каскадно; б) последовательно; в) параллельно; г) последовательно-параллельно. Для каждого способа соединения определить А – параметры сложного ЧП.
соединены разными способами: а) каскадно; б) последовательно; в) параллельно; г) последовательно-параллельно. Для каждого способа соединения определить А – параметры сложного ЧП.
|
| Решение
Так как ЧП одинаковые и симметричные, определим А – параметры одного из ЧП.
Для Т – образной схемы  коэффициенты ЧП найдем через из собственные сопротивления: коэффициенты ЧП найдем через из собственные сопротивления: 
|




В матричной форме коэффициенты ЧП можно задать следующим образом:

При каскадном соединении ЧП матрица результирующего ЧП определяется произведением матриц каскадно-соединенных ЧП:

Из анализа результирующей матрицы следует, что:


Проверяем правильность определения коэффициентов ЧП, используя уравнение их связи: 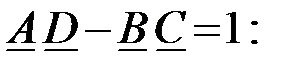
 При последовательном соединении ЧП целесообразно использовать Z – форму записи уравнений ЧП. Для этого определим коэффициенты Z – формы одного симметричиного ЧП:
При последовательном соединении ЧП целесообразно использовать Z – форму записи уравнений ЧП. Для этого определим коэффициенты Z – формы одного симметричиного ЧП:

В матричной форме Z коэффициенты ЧП можно записать как:

При последовательном соединении ЧП матрица результирующего ЧП будет определяться суммой матриц сопротивлений последовательно соединенных ЧП:

Таким образом, из полученной обобщенной матрицы следует, что:


Определим А – параметры сложного четырехполюсника и правильность нахождения коэффициентов с помощью уравнения связи коэффициентов ЧП  для последовательного соединения:
для последовательного соединения:


При параллельном соединении целесообразно использовать Y –форму записи уравнений ЧП. Определим коэффициенты Y – формы одного симметричиного ЧП:
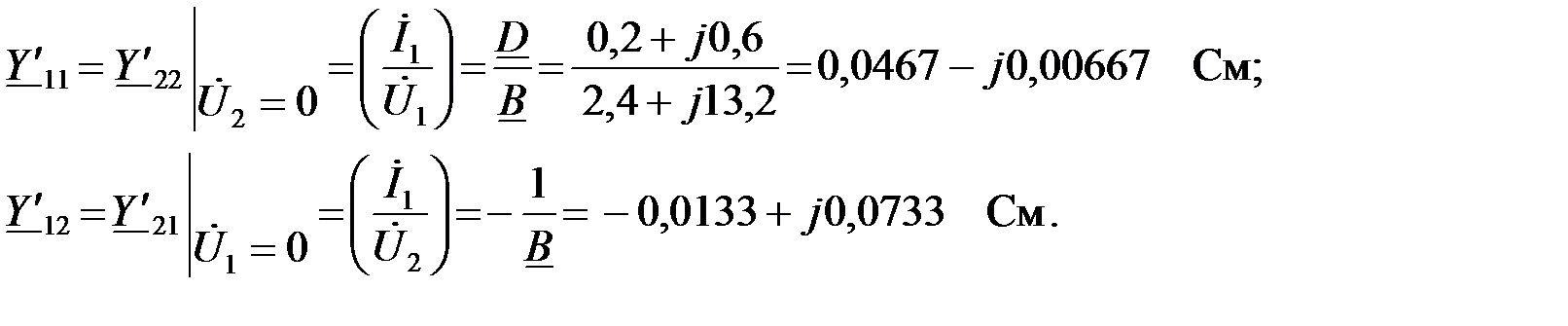
В матричной форме Y коэффициенты одного ЧП можно записать как:

При параллельном соединении ЧП матрица результирующего ЧП определяется суммой матриц проводимостей параллельно соединенных ЧП:

Из анализа полученной обобщенной матрицы следует, что:

Тогда определитель Y─ формы составного ЧП может быть найден как:
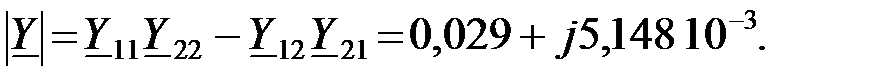
Определим А – параметры сложного ЧП и правильность нахождения коэффициентов с помощью уравнения связи коэффициентов ЧП:  для параллельно соединенных ЧП:
для параллельно соединенных ЧП:
 Тогда, используя уравнения связи коэффициентов ЧП, проверяем правильность их определения.
Тогда, используя уравнения связи коэффициентов ЧП, проверяем правильность их определения.

При последовательно-параллельном соединении целесообразно использовать H – форму записи уравнений ЧП. Определим коэффициенты H – формы одного симметричного ЧП:


В матричной форме Н коэффициенты ЧП могут представлены следующим образом:

При последовательно-параллельном соединении ЧП матрица результирующего ЧП определяется суммой матриц H - параметров последовательно-параллельно соединенных ЧП:
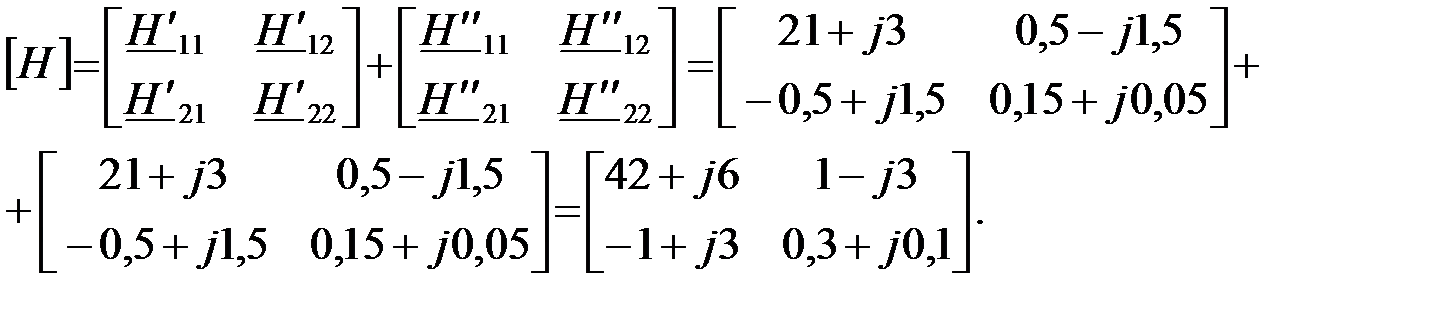
Из анализа полученной обобщенной матрицы следует, что:

Тогда определитель Н формы составного ЧП имеет вид:

Определим А – параметры сложного ЧП и правильность нахождения коэффициентов с помощью уравнения связи коэффициентов ЧП:  для последовательно-параллельного соединения:
для последовательно-параллельного соединения:
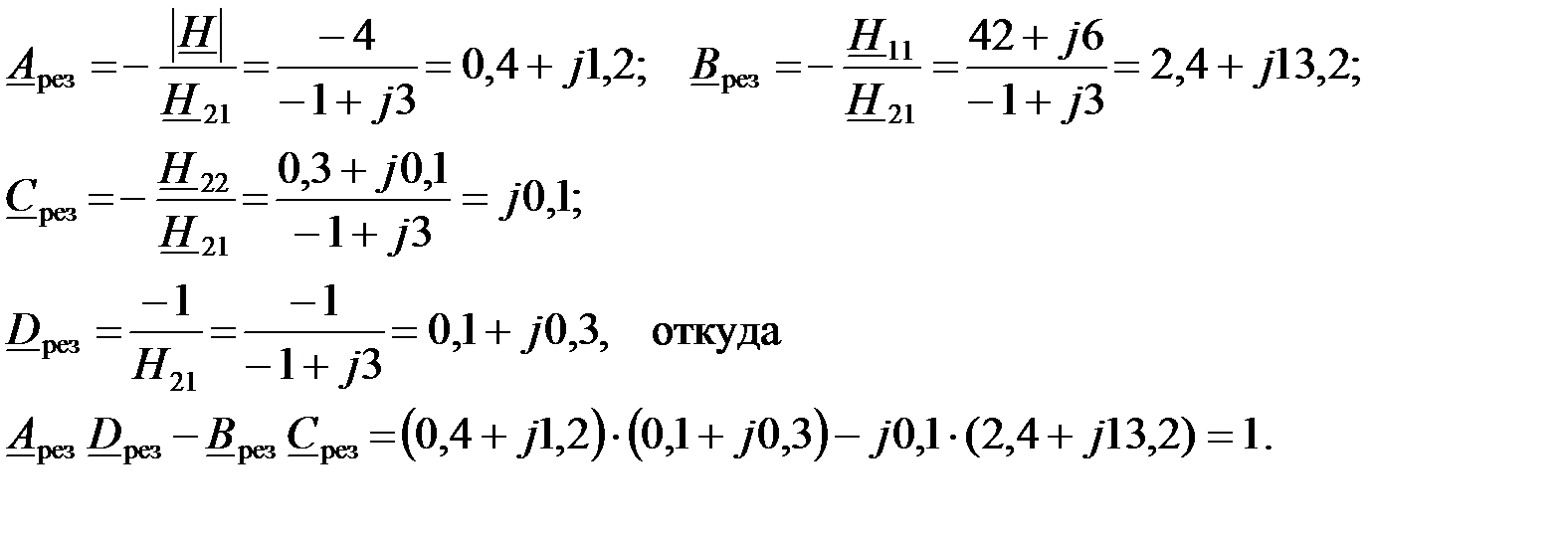
Задача 2.3.4 Два одинаковых четырехполюсника (рис.2.3.4) с параметрами  соединены каскадно. Определить
соединены каскадно. Определить  – коэффициенты сложного ЧП.
– коэффициенты сложного ЧП.
Решение
Так как ЧП одинаковые, то у них:

|
Определим 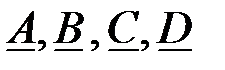 коэффициенты, используя Т – образную схему замещения ЧП:
коэффициенты, используя Т – образную схему замещения ЧП:

Осуществим проверку правильности расчета  коэффициентов, используя уравнение их связи:
коэффициентов, используя уравнение их связи:

В матричной форме:

Найдем матрицу коэффициентов результирующего ЧП:

Задача 2.3.5 Два одинаковых ЧП (рис.2.3.5) с параметрами 

 соединены последовательно. Определить Z – параметры сложного ЧП.
соединены последовательно. Определить Z – параметры сложного ЧП.
Решение
Определим Z –
параметры одного из ЧП:

|


Запишем в матричной форме Z – параметры одного из ЧП:

Выразим Z – параметры сложного ЧП в матричной форме:

Таким образом, Z – параметры сложного ЧП имеют следующие значения:

Определитель Z – формы составного ЧП:

Определим правильность расчетов  коэффициентов из уравнения связи:
коэффициентов из уравнения связи: 
Для этого найдем  коэффициенты сложного ЧП:
коэффициенты сложного ЧП:


Осуществим проверку расчета коэффициентов ЧП:
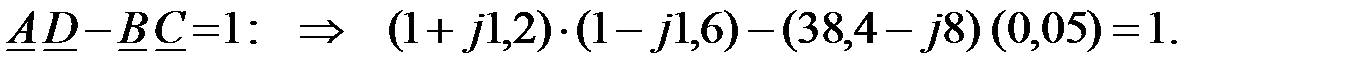
Расчет выполнен верно.
Задача 2.3.6 Два одинаковых ЧП (рис.2.3.6) с параметрами  соединены параллельно. Определить Y – параметры сложного ЧП.
соединены параллельно. Определить Y – параметры сложного ЧП.
Решение
Коэффициенты Y – формы записи уравнений ЧП можно определить через  коэффициенты или собственные сопротивления ветвей схемы ЧП. коэффициенты или собственные сопротивления ветвей схемы ЧП.
|
Так как четырехполюсники можно представить Т – образной схемой замещения, то проще вначале  коэффициенты через собственные сопротивления ЧП:
коэффициенты через собственные сопротивления ЧП:




Выполним проверку расчета коэффициентов с помощью уравнения связи коэффициентов  :
: 
Определим коэффициенты Y – формы для одного из четырехполюсников:




В матричной форме коэффициенты Y – формы составного ЧП:

При параллельном соединении ЧП, матрица результирующего ЧП определяется суммой матриц параллельно включенных ЧП:

Таким образом Y – параметры сложного ЧП имеют следующие значения:

Тогда в матричной форме Y – параметры составного ЧП найдены как:

Определяем правильность расчета 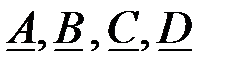 коэффициентов ЧП с помощью уравнения связи коэффициентов:
коэффициентов ЧП с помощью уравнения связи коэффициентов: 
Для этого выразим  коэффициенты ЧП через Y-параметры
коэффициенты ЧП через Y-параметры
 Осуществим проверку расчета
Осуществим проверку расчета  коэффициентов:
коэффициентов:

Задача 2.3.7 Два одинаковых ЧП (рис.2.3.7) с параметрами  соединены последовательно–параллельно. Определить H – параметры сложного ЧП.
соединены последовательно–параллельно. Определить H – параметры сложного ЧП.
Решение
Так как ЧП одинаковые, определим А – параметры одного из ЧП. Для Т– образной схемы ЧП  коэффициенты найдем через собственные сопротивления ЧП: коэффициенты найдем через собственные сопротивления ЧП: 
|

Вычислим коэффициенты H – формы через 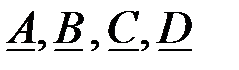 коэффициенты одного ЧП:
коэффициенты одного ЧП:

 В матричной форме Н – коэффициенты ЧП имеют вид:
В матричной форме Н – коэффициенты ЧП имеют вид:

При последовательно-параллельном соединении ЧП матрица результирующего ЧП определяется суммой матриц последовательно-параллельно соединенных ЧП:

Таким образом Н – параметры сложного ЧП имеют следующие значения:

Определитель Н – формы составного ЧП найдем как:

Определим А – параметры сложного ЧП и правильность нахождения коэффициентов с помощью соотношения  для последовательно-параллельного соединения:
для последовательно-параллельного соединения:

Проводим проверку правильности определения  коэффициентов:
коэффициентов:

Расчет коэффициентов выполнен правильно.
Задача 2.3.8 Два одинаковых ЧП (рис.2.3.8) с параметрами 

 соединены параллельно – последовательно. Определить G – параметры сложного ЧП.
соединены параллельно – последовательно. Определить G – параметры сложного ЧП.
Решение
Представим параллельно-последовательно соединенные четырехполюсники Т – образными схемами замещения с сопротивлениями:
 
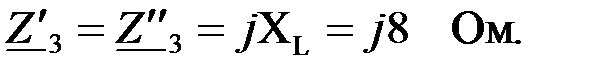
|
Т.к. ЧП одинаковые, определим А – параметры одного из четырехполюсников. Для Т – образной схемы 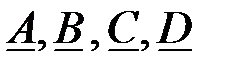 коэффициенты найдем через собственные сопротивления схемы ЧП:
коэффициенты найдем через собственные сопротивления схемы ЧП:
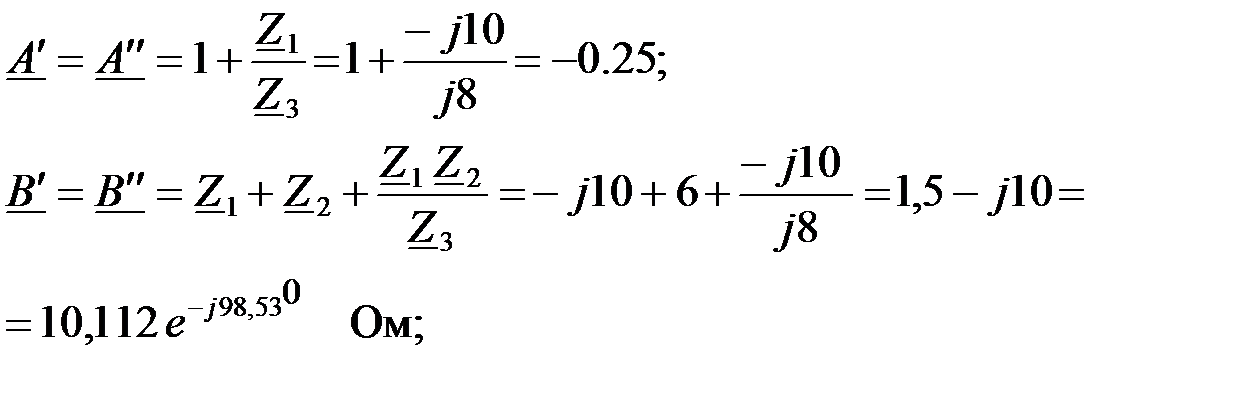

Выполним проверку нахождения  коэффициентов ЧП:
коэффициентов ЧП:

Выразим коэффициенты G – формы записи через  коэффициенты ЧП:
коэффициенты ЧП:
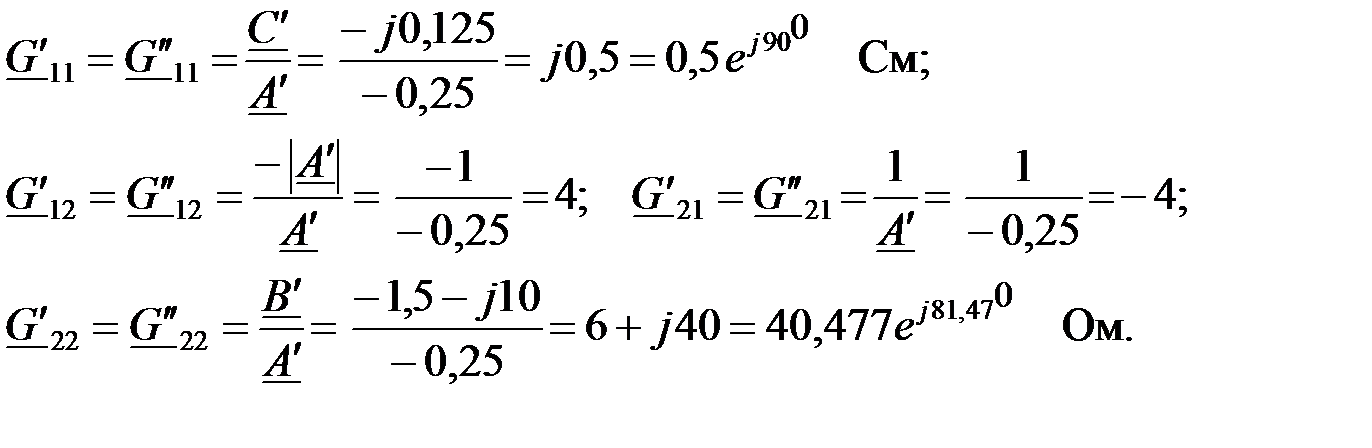
В матричной форме G коэффициенты ЧП будут иметь вид:

При параллельно – последовательном соединении ЧП, матрица результирующего ЧП определяется суммой матриц отдельных ЧП:


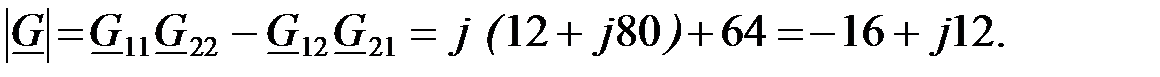
Вычислим  коэффициенты результирующего ЧП:
коэффициенты результирующего ЧП:

Выполним проверку нахождения 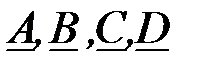 коэффициентов ЧП с использованием уравнения их связи:
коэффициентов ЧП с использованием уравнения их связи: 
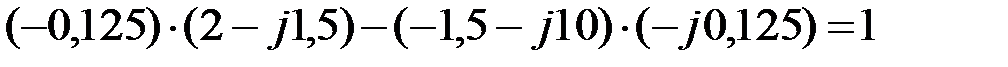
Расчет выполнен верно.
Дата добавления: 2015-10-21; просмотров: 170 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение | | | Решение |