Электрические фильтры 3 страница

Рис. 3.3.5,б

Найдем токи в элементах ПФ:

Определим падение напряжения в последовательном звене ПФ и выходное напряжение 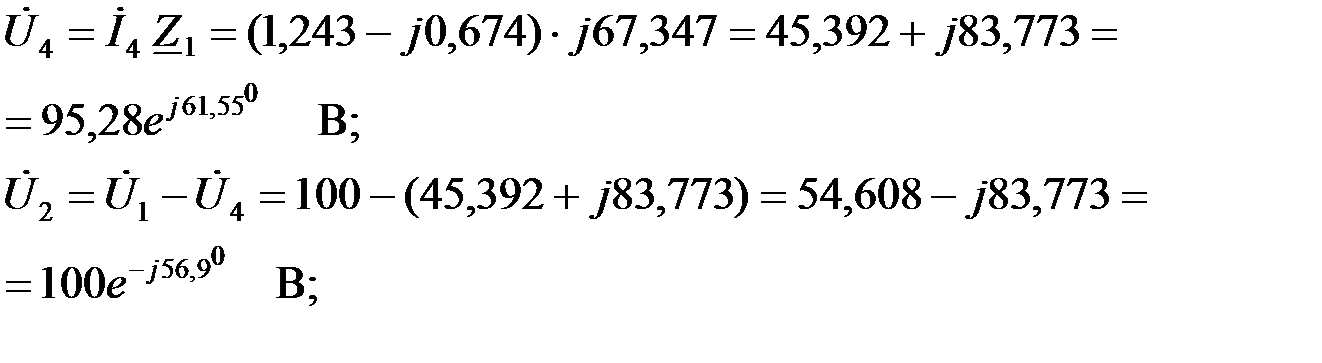Рассчитать токи в параллельном выходном элементе ПФ и на выходе фильтра (рис.3.3.5,б):  

Векторная диаграмма токов и напряжений ПФ на рис.3.3.5,в.

Рис.3.3.5,в

Зависимости коэффициента затухания , коэффициента фазы , и характеристического сопротивления в функции частоты выражаются следующим образом:

Графические зависимости, , и показаны на рис.3.3.5.г,д,е.

Рис.3.3.5,г  

Рис.3.3.5,д

Рис.3.3.5,е

3.4 Заграждающие фильтры типа «k»

Задача 3.4.1 Определить полосу затухания заграждающего фильтра (ЗФ), представленного на рис.3.4.1, если параметры элементов фильтра известны:

Рис.3.4.1

Решение Полоса затухания заграждающих фильтров, определяется соотношением[1,8]: Откуда:

Задача 3.4.2 Определить полосу пропускания ЗФ, представленного на рис.3.4.2, если параметры элементов фильтра известны:

Рис.3.4.2

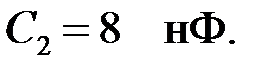
Решение Полосу затухания ЗФ можно определить, используя соотношение [1,8]:

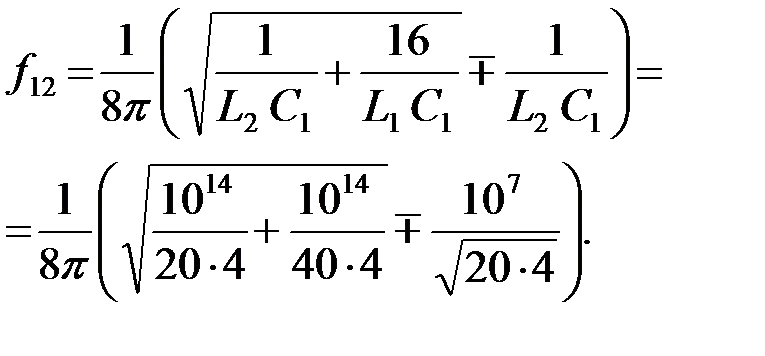
Откуда:

Задача 3.4.3 Определить параметры элементов заграждающего фильтра, собранного по П – образной схеме, если нижняя частота среза равна 20 кГц, а верхняя 100 кГц, номинальное характеристическое волновое сопротивление =500 Ом. Найти характеристическое сопротивление фильтра на частотах: Построить зависимости характеристического сопротивления , коэффициента затухания «α» и коэффициента фазы «β» от частоты. Рассчитать токи и напряжения на заданной частоте и построить векторную диаграмму токов и напряжений в элементах ЗФ, если входной ток равен 0,5 А.

Рис.3.4.3, а

Решение Схема заграждающего фильтра, собранного по П – образной схеме, приведена на рис.3.4.3. Зная граничные частоты и характеристическое номинальное волновое сопротивление , можно определить значения индуктивностей и емкостей фильтра:

Характеристическое сопротивление определяется следующим образом [1,8]:

где

Рассчитаем характеристические сопротивления на заданных по условию задачи частотах.

На частоте :

На частоте

На частоте

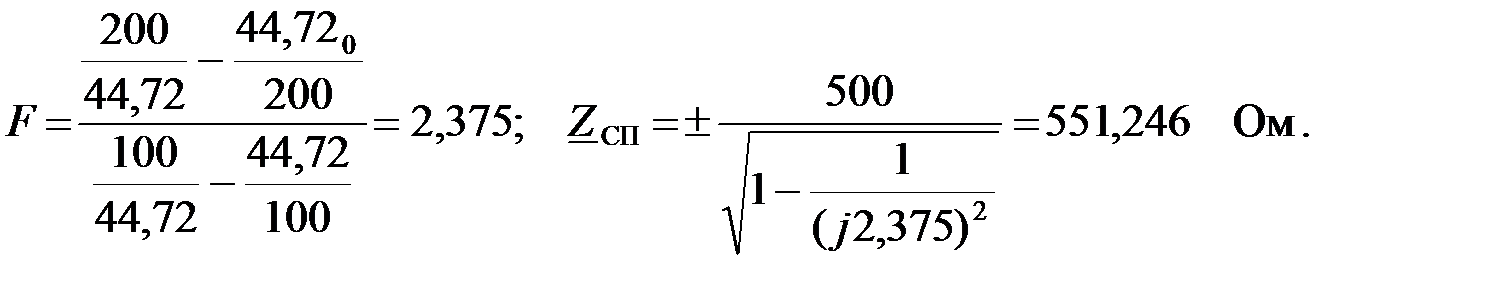
Для построения графической зависимости характеристического сопротивления, в функции частоты воспользуемся выражением [1,8]:

Коэффициент затухания в полосе пропускания равен нулю, а в полосе затухания определяется соотношением: . Коэффициент фазы в полосе пропускания равен: , а в полосе затухания: где . Графические зависимости характеристического сопротивления, коэффициента затухания и коэффициента фазы от частоты приведены на рис 3.4.3, б, в, г.

	Рис.3.4.3,б
Рис.3.4.3,в
Рис.3.4.3,г

Схема замещения ЗФ для расчёта токов и напряжений приведена на рис.3.4.3,д.

Определим комплексные сопротивления

Для чего вначале найдем сопротивления отдельных элементов ЗФ:

Рис.3.4.3,д

Тогда сопротивления звеньев ЗФ в схеме замещения на рис.3.4.3,д:

Рассчитаем токи и напряжения на обобщенных элементах заграждающего фильтра, используя характеристическое сопротивление .

Вначале, используя характеристическое сопротивление и входной ток , найдем входное напряжение ЗФ 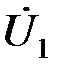, а затем ток в параллельном входном сопротивлении :

В соответствии с первым законом Кирхгофа найдем ток , а затем определим падение напряжения в последовательном сопротивлении ЗФ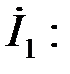

Вычислим выходное напряжение и ток в выходном параллельном сопротивлении

Рис.3.4.3,е

Использупервый закон Кирхгофа, найдем выходной ток ЗФ 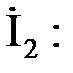Векторная диаграмма токов и напряжений ЗФ показана на рис.3.4.3,е.

Задача 3.4.4 Определить характеристические параметры заграждающего фильтра, собранного по Т – образной схеме (рис.3.4.4.а) на частоте 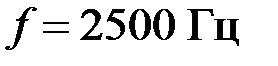если параметры элементов ЗФ: Вычислить токи и напряжения на элементах ЗФ, если входное напряжение Построить векторную диаграмму токов и падений напряжений на заданной частоте, а также графические зависимости коэффициента затухания «α», коэффициента фазы «β» и характеристического сопротивления в функции частоты.

Рис. 3.4.4,а

Решение Определим волновое номинальное характеристическое сопротивление фильтра:

Полоса задерживания заграждающих фильтров, определяется соотношением [8]:

Откуда получаем частоты , и находим резонансную частоту ЗФ:

Вычисляем нормированную частоту ЗФ:

Тогда характеристическое сопротивление ЗФ:

Коэффициент фазы:

Для определения токов и напряжений элементов фильтра строим схему замещения ЗФ (рис.3.4.4,б), и рассчитываем сопротивления звеньев фильтра на заданной частоте:

Рис.3.4.4,б

Находим токи в элементах ЗФ: а) входной ток по закону Ома: б) ток найдем из решения уравнения составленного по второму закону Кирхгофа для входного контура:

в) Выходной ток находим в соответствии с первым законом Кирхгофа:

Для выходного контура составим уравнение по второму закону Кирхгофа и найдем выходное напряжение ЗФ:

Зная токи и сопротивления, вычисляем падения напряжений в элементах ЗФ:

Рис.3.4.4,в	Векторная диаграмма показана на рис. 3.4.4,в. Зависимость коэффициента фазы от частоты: приведена на рис 3.4.4,г. Зависимость коэффициента затухания от частоты: приведена на рис.3.4.4,д. Зависимость характеристического сопротивления от частоты: , приведена на рис.3.4.4,е.
Рис.3.4.4,г	Рис.3.4.4,д
Рис.3.4.4,е

3.5 Производные фильтры типа «m»

Задача 3.5.1 Определить параметры производного Г – образного фильтра низкой частоты типа «m», представленный на рис.3.5.1,а, прототипом которого, является Г – образный фильтр типа «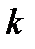», если m =0,6; k =300 Ом; . Рассчитать характеристические сопротивления фильтра на и коэффициент затухания на частотах

Построить зависимость характеристического сопротивления от частоты со стороны параллельного звена ФНЧ.

Рис.3.5.1,а

Решение Определим элементы ФНЧ типа «k»:

Рассчитаем параметры элементов Г – образного звена фильтра типа «m»:

Найдем характеристические сопротивления Г – образного производного фильтра на заданных частотах со стороны параллельного и последовательного звеньев (рис.3.5.1,а).

Характеристическое сопротивление можно найти следующим образом [8]:

а характеристическое сопротивление 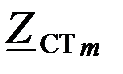как: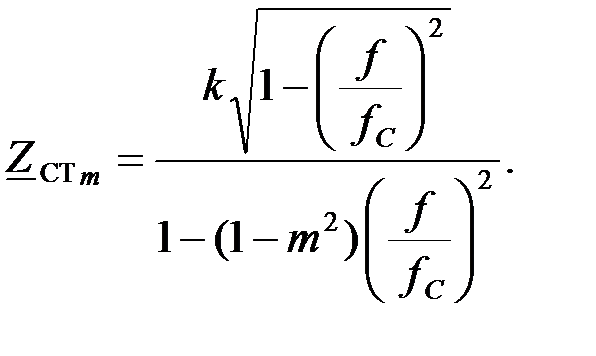

Вычислим частоту бесконечного затухания:

Таким образом, частота оказывается меньше частоты бесконечного затухания «α», а характеристическое сопротивление на данной частоте имеет индуктивный характер.

Характеристические сопротивления и на частоте будут равны:

В полосе пропускания 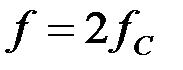характеристические

сопротивления 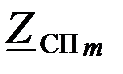и должены иметь активный характер.

Рассчитаем их значения:

Коэффициент затухания «» на частоте будет определяться следующим образом:

Задача 3.5.2 Определить полосу пропускания Г – образного фильтра низкой частоты типа «m», представленного на рис.3.5.2, а, прототипом которого, является Г – образный фильтр типа «», если m = 0,65; если Определить значения сопротивлений фильтра типа «m» и найти характеристическое сопротивление фильтра на частоте Построить зависимость характеристического сопротивления от частоты.

Рис.3.5.2,а

Решение Данный фильтр типа «m» является параллельно – производным от Г – образного фильтра низкой частоты типа «k». Полосы пропускания фильтров типа «k» и типа «m» совпадают, это значит, что частоту среза ФНЧ можно найти как:

Рассчитаем параметры элементов Г – образного звена фильтра типа «m»:

Определим сопротивления звеньев фильтра на частоте

Характеристические сопротивления прототипа и фильтра типа «m» совпадают. Рассчитаем их значения:

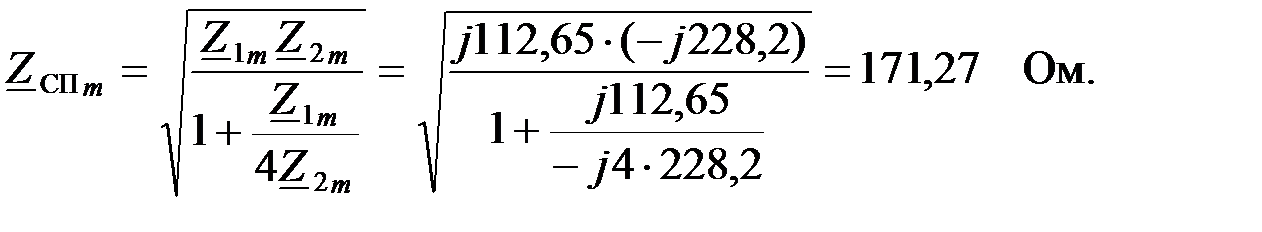
Характеристическое сопротивление для параллельно-производного звена будет определяться следующим соотношением [8]:

Рис.3.5.2,б

Зависимость характеристического сопротивления показана на рис.3.5.2,б.

Задача 3.5.3 Определить полосу пропускания фильтра высокой частоты типа «m», представленного на рис.3.5.2, а, прототипом которого, является Г – образный фильтр типа «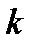», если m =0,5; Найти значения сопротивлений звеньев фильтра типа «m», характеристическое сопротивление фильтра 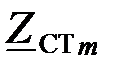и коэффициент фазы «β» на частоте 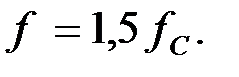Построить графическую зависимость характеристического сопротивления от частоты.

Рис.3.5.3,а

Решение Данный фильтр является последовательно – производным, частота среза которого определяется из выражения: Рассчитаем параметры элементов фильтра типа «m»:

Характеристические сопротивление фильтра прототипа и производного фильтра типа «m» совпадают и могут быть определены на частоте из следующего выражения:

Характеристическое сопротивление на указанной частоте можно определить как [8]:

Рис.3.5.3,б

Зависимость характеристического сопротивления показана на рис.3.5.3,б.

Коэффициент фазы в полосе пропускания найдем следующим образом [8]:

Задача 3.5.4 Определить параметры параллельно – производного Г– образного звена фильтра высокой частоты типа «m», представленного на рис.3.5.4, а, прототипом которого, является Г– образный фильтр типа «», если m = 0,542; номинальное волновое характеристическое сопротивление k =200 Ом, а частота среза . Определить характеристические сопротивления фильтра на частотах и значения коэффициента затухания «α» на частотах:

Рис.3.5.4,а

Решение Определим параметры элементов фильтра прототипа:

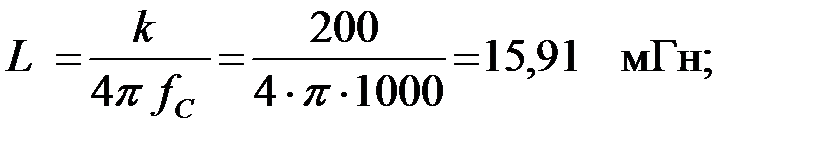
Определим параметры элементов Г – образного звена ФВЧ типа «m»:

Найдем характеристические сопротивления и на заданных частотах (рис.3.5.4) согласно [8].

Характеристическое сопротивление производного Г – образного фильтра со стороны параллельного звена (рис.3.5.4,а) будет определяться из выражения:

Характеристическое сопротивление производного Г – образного фильтра со стороны последовательного звена (рис.3.5.4,а) определяется из выражения:

Тогда для частоты :

Найдем частоту бесконечного затухания:

При частоте фильтр находится на частоте бесконечно большого затухания, в силу чего характеристическое сопротивление изменяет характер с емкостного на индуктивный и будет равно:

Дата добавления: 2015-10-21