
Читайте также:
|
Задача 2.6.1 У четырехполюсника, представленного на рисунке 2.6.1,а заданы следующие параметры: 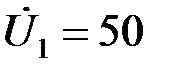 В;
В;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом. Определить
Ом. Определить  коэффициенты и записать уравнение в А – форме, вычислить сопротивления и построить Т и П – схемы замещения. Найти характеристические параметры ЧП. Построить круговую диаграмму для тока
коэффициенты и записать уравнение в А – форме, вычислить сопротивления и построить Т и П – схемы замещения. Найти характеристические параметры ЧП. Построить круговую диаграмму для тока  , при изменении по модулю сопротивления нагрузки.
, при изменении по модулю сопротивления нагрузки.
Решение:
Для определения  коэффициентов, вычислим сопротивления холостого хода и короткого замыкания со стороны зажимов «mn» и «pq»: коэффициентов, вычислим сопротивления холостого хода и короткого замыкания со стороны зажимов «mn» и «pq»:
|


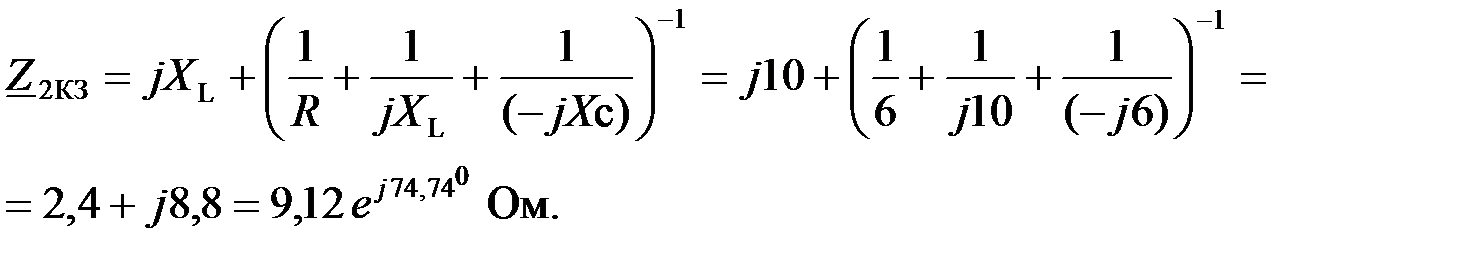
Правильность определения сопротивлений проверяем с помощью соотношения:

Откуда получаем тождество:

Тогда  коэффициенты можно вычислить по сопротивлениям холостого хода и короткого замыкания:
коэффициенты можно вычислить по сопротивлениям холостого хода и короткого замыкания:
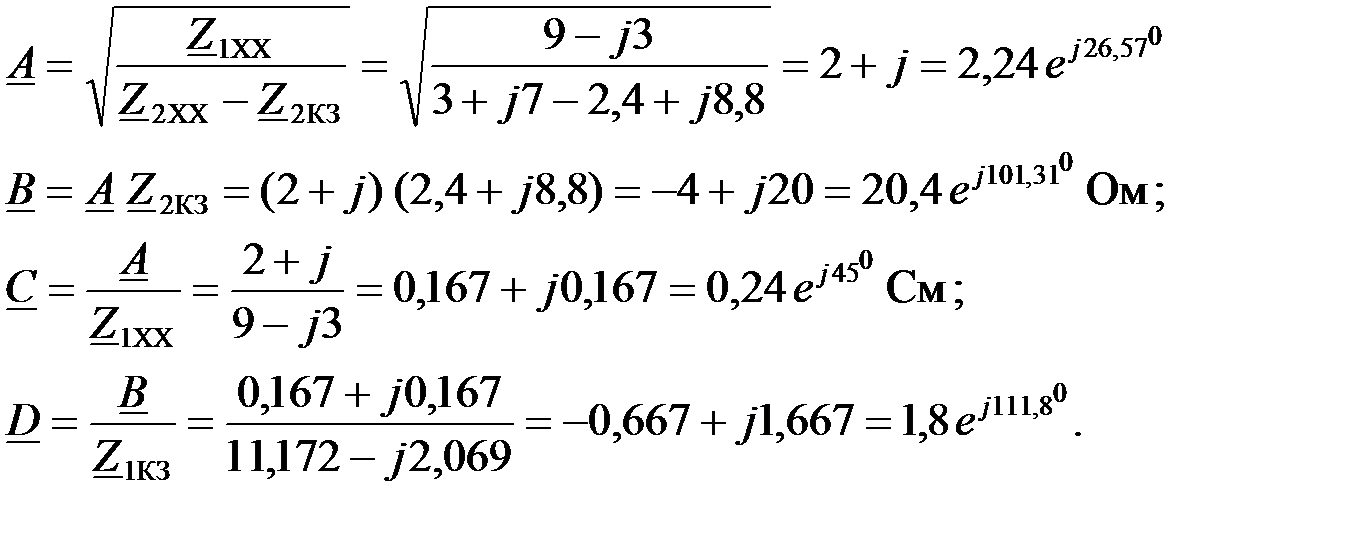
Осуществим проверку определения  коэффициентов, используя уравнения их связи:
коэффициентов, используя уравнения их связи:
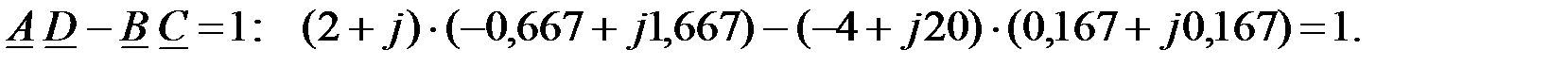
Зная 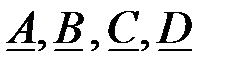 коэффициенты, запишем уравнения четырехполюсника в А – форме:
коэффициенты, запишем уравнения четырехполюсника в А – форме:

Вычислим сопротивления и построим Т и П – образные схемы замещения:
1) Для Т – образной схемы:

Т – образная схема замещения приведена на рисунке 2.6.1,б.
2) Для П – образной схемы:


П – образная схема замещения приведена на рисунке 2.6.1,в.
Характеристические сопротивление четырехполюсника можно определить по  коэффициентам или сопротивлениям холостого хода и короткого замыкания:
коэффициентам или сопротивлениям холостого хода и короткого замыкания:

Для определения меры передачи ЧП вычислим гиперболические функции:
 откуда
откуда
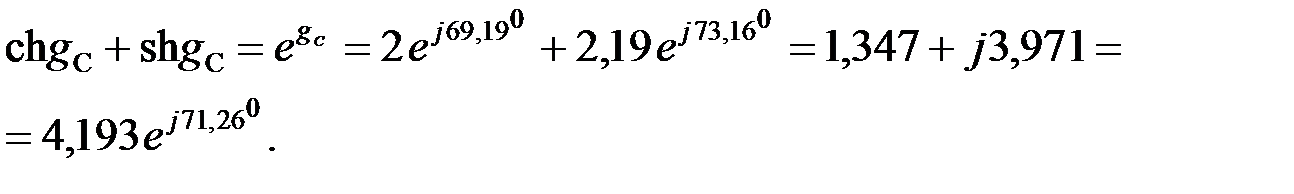
Логарифмируя 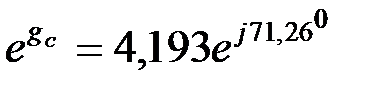 , найдем
, найдем  :
:

откуда 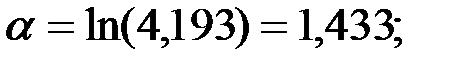

Следовательно, меру передачи можно выразить следующим образом:

Зная характеристические параметры и меру передачи можно записать уравнение ЧП в гиперболических функциях:

Построим круговую диаграмму для тока  при изменении по модулю сопротивления нагрузки при изменении по модулю сопротивления нагрузки  (рис. 2.6.1,г):
Уравнение круговой диаграммы для тока
(рис. 2.6.1,г):
Уравнение круговой диаграммы для тока  записывается следующим образом: записывается следующим образом:

|
Для построения круговой диаграммы определим ток  :
:

Записываем уравнение круговой диаграммы для тока  с учетом
с учетом  :
:

Построение круговой диаграммы показано на рис. 2.6.1,д.
Проведем проверку правильности построения диаграммы, например, для значения сопротивления нагрузки 
 Данные значения совпадают с вектором тока на круговой диаграмме.
Данные значения совпадают с вектором тока на круговой диаграмме.
|
Задача 2.6.2 Для ЧП представленного на рисунке 2.6.2,а заданы следующие параметры:  В;
В; 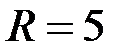 Ом;
Ом; 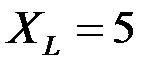 Ом;
Ом;  Ом;
Ом;  Ом. Определить
Ом. Определить  коэффициенты и записать уравнение в А
коэффициенты и записать уравнение в А  форме, вычислить сопротивления холостого хода и короткого замыкания и построить Т и П
форме, вычислить сопротивления холостого хода и короткого замыкания и построить Т и П  образные схемы замещения ЧП. Найти характеристические параметры
образные схемы замещения ЧП. Найти характеристические параметры  и вычислить передаточные функции ЧП. Построить круговую диаграмму для тока
и вычислить передаточные функции ЧП. Построить круговую диаграмму для тока  , при изменении по модулю сопротивления нагрузки
, при изменении по модулю сопротивления нагрузки 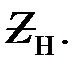
Решение:
Для определения 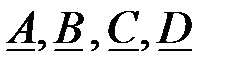 коэффициентов ЧП, вычислим сопротивления холостого хода и короткого замыкания со стороны зажимов «mn» и «pq»: коэффициентов ЧП, вычислим сопротивления холостого хода и короткого замыкания со стороны зажимов «mn» и «pq»:
|
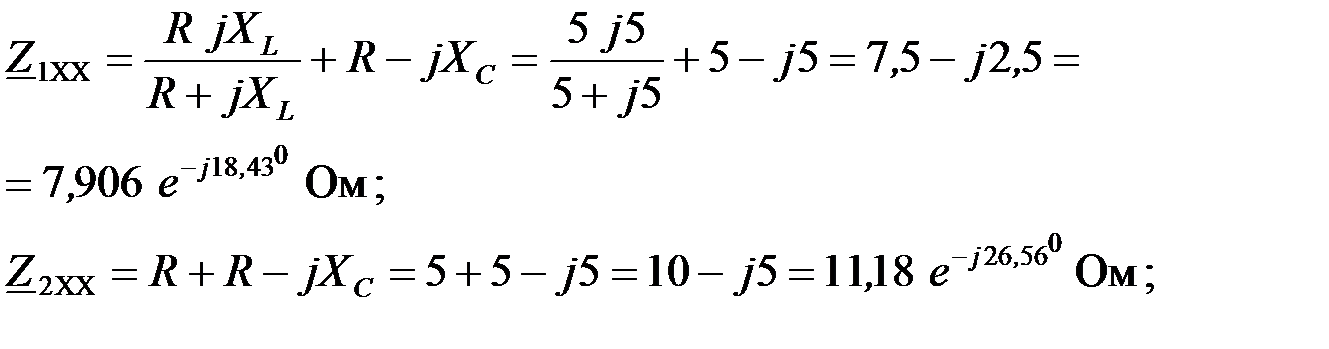

Правильность определения сопротивлений проверяем с помощью соотношения:

Откуда получаем тождество 
Тогда  коэффициенты можно вычислить по сопротивлениям холостого хода и короткого замыкания:
коэффициенты можно вычислить по сопротивлениям холостого хода и короткого замыкания:

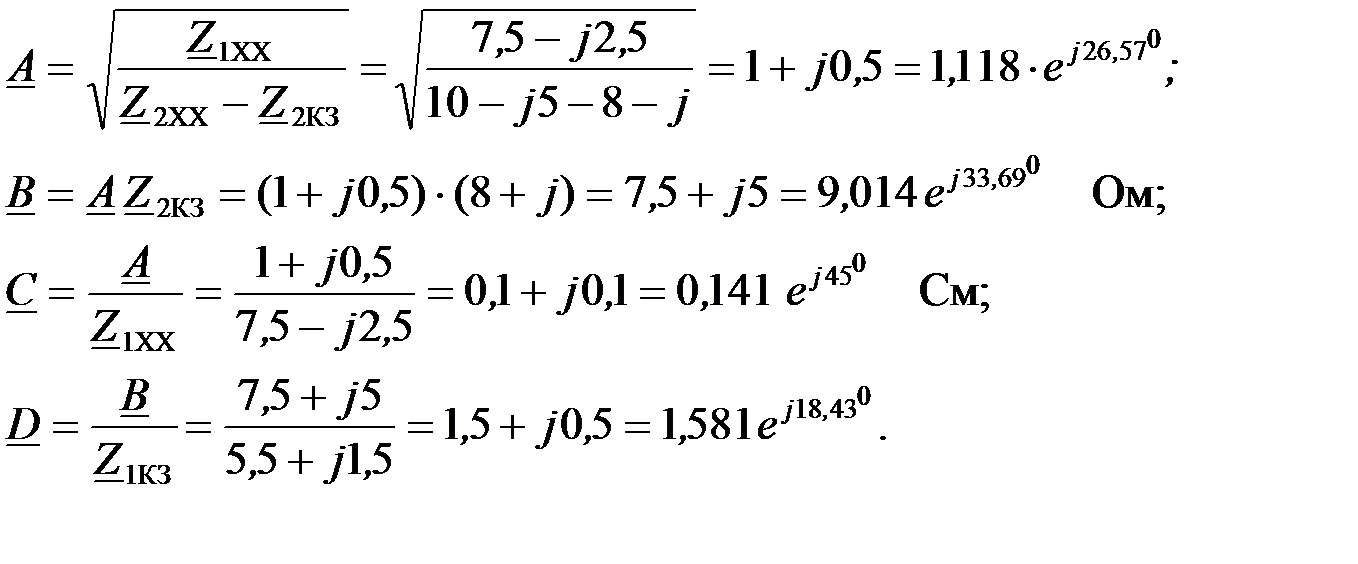
Осуществляем проверку правильности расчета  коэффициентов из уравнения их связи:
коэффициентов из уравнения их связи: 
Зная  коэффициенты, запишем уравнение ЧП в А
коэффициенты, запишем уравнение ЧП в А  форме:
форме:

Вычислим собственные сопротивления звеньев и построим Т и П – образные схемы замещения:
1) Т – образная схема замещения:

|
Т – образная схема замещения приведена на рис. 2.6.2,б.
2) П – образная схема замещения:
 П – образная схема замещения приведена на рис. 2.6.2,в. П – образная схема замещения приведена на рис. 2.6.2,в.
|
Характеристические сопротивление ЧП можно определить по коэффициентам 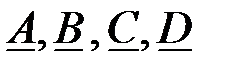 ЧП или сопротивлениям холостого хода и короткого замыкания:
ЧП или сопротивлениям холостого хода и короткого замыкания:


Для определения меры передачи вычислим гиперболические функции:
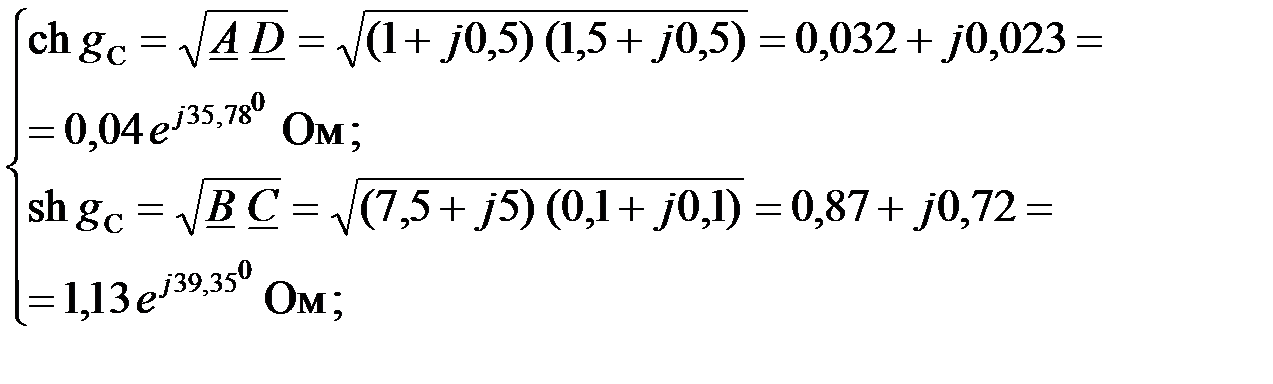
Откуда 
Логарифмируя последнее выражение находим  :
:
 ,
,
откуда 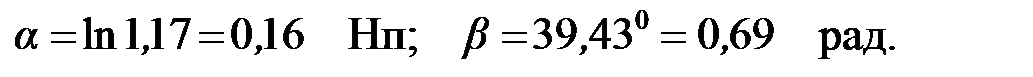
Следовательно, мера передачи  может быть представлена следующим образом:
может быть представлена следующим образом:

Зная характеристические параметры и меру передачи можно записать уравнение ЧП в гиперболических функциях:

Для нахождения передаточных функций ЧП воспользуемся П – образной схемой замещения и найдем токи на входе цепи ( ) и в нагрузке (
) и в нагрузке ( ), а также напряжение на выходе (
), а также напряжение на выходе ( ). Но, вначале определим эквивалентное сопротивление ЧП со стороны зажимов «mn».
). Но, вначале определим эквивалентное сопротивление ЧП со стороны зажимов «mn».
Схема для расчета токов и напряжений приведена на рисунке 2.6.2,г.


|

Передаточные функции ЧП найдем, используя отношение выходных величин к входным, которые выразим используя  коэффициенты:
коэффициенты:



Построим круговую диаграмму для тока  , при изменении по модулю сопротивления нагрузки
, при изменении по модулю сопротивления нагрузки  Запишем уравнение круговой диаграммы для тока
Запишем уравнение круговой диаграммы для тока  :
:


С учетом полученных выше соотношений запишем уравнение круговой диаграммы для тока  :
:
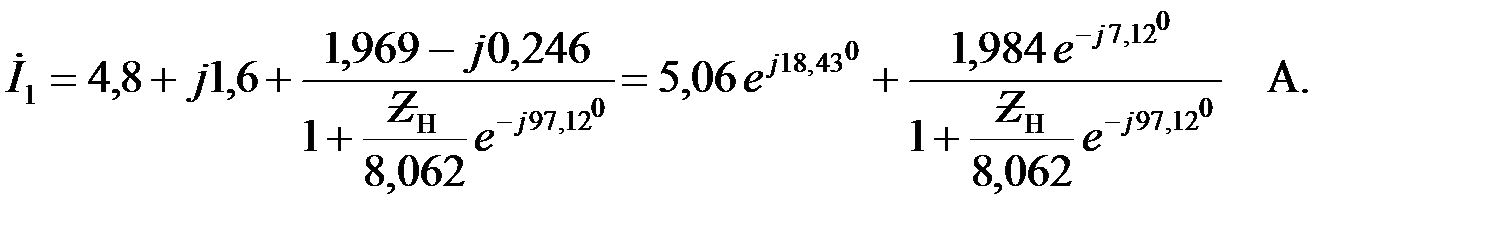
На комплексной плоскости (рис. 2.6.2,д) в масштабе откладываем векторы входного напряжения  и токов
и токов  и
и  . Находим разность векторов токов
. Находим разность векторов токов  и
и  , которая является хордой круговой диаграммы AN. Из конца хорды, в точке N под углом
, которая является хордой круговой диаграммы AN. Из конца хорды, в точке N под углом  откладывает касательную к окружности. Из середины хорды AN и в точке N лежащей на касательной восстановливаем перпендикуляр и находим центр круговой диаграммы
откладывает касательную к окружности. Из середины хорды AN и в точке N лежащей на касательной восстановливаем перпендикуляр и находим центр круговой диаграммы  . Т.к. вписанный угол
. Т.к. вписанный угол  больше 900, то рабочей частью является большая её часть. Выбираем масштаб сопротивления, и в выбранном масштабе на продолжении хорды AN откладываем значение сопротивления
больше 900, то рабочей частью является большая её часть. Выбираем масштаб сопротивления, и в выбранном масштабе на продолжении хорды AN откладываем значение сопротивления  . Под углом, противоположном вписанному углу
. Под углом, противоположном вписанному углу  , строим линию переменного параметра AN, на которой задаем значение сопротивленая нагрузки
, строим линию переменного параметра AN, на которой задаем значение сопротивленая нагрузки  .
.
Рис.2.6.2,д
Для любогомодуля сопротивления нагрузки находим значение тока  . Например, для значения
. Например, для значения  значение тока будет равно:
значение тока будет равно:

Данное значение совпадает с вектором тока на круговой диаграмме.
Задача 2.6.3 Для ЧП, представленного на рисунке 2.6.3,а заданы следующие параметры: 
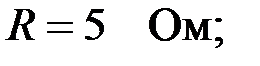
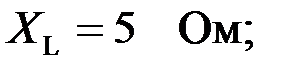

 Требуется определить
Требуется определить  коэффициенты и записать уравнение в А – форме, вычислить сопротивления ветвей и построить Т – и П – образные схемы замещения. Найти характеристические параметры ЧП.
коэффициенты и записать уравнение в А – форме, вычислить сопротивления ветвей и построить Т – и П – образные схемы замещения. Найти характеристические параметры ЧП.
Решение
Для определения  коэффициентов ЧП вычислим сопротивления холостого хода и короткого замыкания для зажимов «mn» и «pq»: коэффициентов ЧП вычислим сопротивления холостого хода и короткого замыкания для зажимов «mn» и «pq»:
|



Тогда  коэффициенты ЧП можно найти по сопротивлениям холостого хода и короткого замыкания:
коэффициенты ЧП можно найти по сопротивлениям холостого хода и короткого замыкания:


 Осуществим проверку
Осуществим проверку  коэффициентов, используя уравнение их связи:
коэффициентов, используя уравнение их связи:

Зная коэффициенты,  запишем уравнение ЧП в А – форме:
запишем уравнение ЧП в А – форме:

Вычислим сопротивления и построим схемы замещения:
1) Т – образная схема замещения:

|

Т – образная схема замещения приведена на рис.2.6.3,б.
2) П – образная схема замещения:
 П – образная схема замещения приведена на рис. 2.6.3,в.
П – образная схема замещения приведена на рис. 2.6.3,в.
|
Характеристические сопротивление четырехполюсника можно определить по  коэффициентам
коэффициентам  или сопротивлениям холостого хода и короткого замыкания:
или сопротивлениям холостого хода и короткого замыкания:

Для определения меры передачи ЧП вычислим гиперболические функции:

Откуда
 .
.
Логорифмируя последнее соотношение, найдем  :
:  ,
,
откуда  Нп;
Нп; 
Следовательно, мера передачи  может быть представлена следующим образом:
может быть представлена следующим образом:
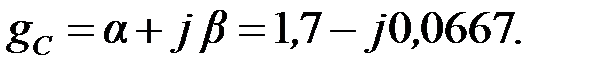
Задача 2.6.4 Для ЧП, представленного на рис.2.6.4,а заданы следующие параметры:  В;
В;  Ом;
Ом;  Ом;
Ом;  Ом. Требуется определить
Ом. Требуется определить  коэффициенты и записать уравнение в А – форме, вычислить сопротивления ветвей и построить Т и П – образные схемы замещения. Найти характеристические параметры. Построить круговую диаграмму для тока
коэффициенты и записать уравнение в А – форме, вычислить сопротивления ветвей и построить Т и П – образные схемы замещения. Найти характеристические параметры. Построить круговую диаграмму для тока  , при изменении по модулю активного сопротивления нагрузки.
, при изменении по модулю активного сопротивления нагрузки.
Решение
Вычислим сопротивления холостого хода и короткого замыкания со стороны зажимов «mn» и «pq»:

|



Тогда  коэффициенты можно найти следующим образом:
коэффициенты можно найти следующим образом:

Осуществим проверку коэффициентов  на основании соотношения:
на основании соотношения:
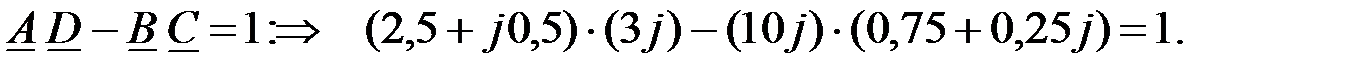
Зная  коэффициенты, запишем уравнение ЧП в А – форме:
коэффициенты, запишем уравнение ЧП в А – форме:

Вычислим собственные сопротивления ветвей и построим Т и П – образные схемы замещения:
1) Т – образная схема замещения:

|
Т – образная схема замещения приведена на рис. 2.6.4,б.
2) П – образная схема замещения:
 П – образная схема замещения приведена на рис. 2.6.4,в.
П – образная схема замещения приведена на рис. 2.6.4,в.
|
Определим характеристические параметры ЧП:
Характеристические сопротивления ЧП рассчитаем через 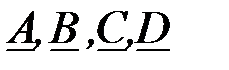 коэффициенты
коэффициенты

Мера передачи:

Логарифмируя последовательное уравнение, найдем  :
:

Следовательно, меру передачи можно задать следующим образом:

Построим круговую диаграмму для тока  при изменении по модулю сопротивления нагрузки. Для этого найдем ток
при изменении по модулю сопротивления нагрузки. Для этого найдем ток  используя Т-схему замещения:
используя Т-схему замещения:

Тогда, уравнение круговой диаграммы для тока  , с учетом
, с учетом  , запишем как:
, запишем как:

Круговая диаграмма тока  приведена на рис. 2.6.4,д.
приведена на рис. 2.6.4,д.
Проведем проверку правильности построения круговой диаграммы для нескольких значений сопротивлений нагрузки:

|

Данные значения совпадают с вектором тока на круговой диаграмме.
2.7 Задачи для самостоятельного решения
Задача 2.7.1 Для ЧП представленного на рис.2.7.1 определить коэффициенты А, Zи Y – форм записи, если: 
| |
Задача 2.7.2 Для ЧП представленного на рис.2.7.2 определить коэффициенты А, B, Z, Y, G, H – форм записи, если:  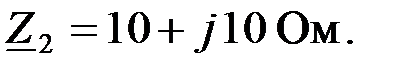
| |
Задача 2.7.3 Для ЧП, представленного на рис.2.7.3 определить коэффициенты А, B, Z, Y, G, H – форм записи, если: 
| |
Задача 2.7.4 Для ЧП, представленного на рис.2.7.4 определить коэффициенты А, B, Z, Y, G, H – форм записи, если:  
| |
Задача 2.7.5 Для ЧП представленного на рис.2.7.5 определить коэффициенты А, B, Z, Y, G, H – форм записи, если:
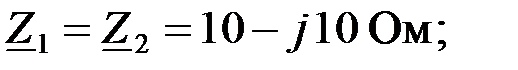 
|
Задача 2.7.6 Известны А – параметры ЧП:  Определить Y и Z – параметры.
Определить Y и Z – параметры.
Задача 2.7.7 Известны коэффициенты симметричного ЧП:  Определить коэффициенты Z, Y, G, H – форм записи.
Определить коэффициенты Z, Y, G, H – форм записи.
Задача 2.7.8 Известны Z – коэффициенты ЧП:
 Определить А, В, С, D коэффициенты в А и В формах записи.
Определить А, В, С, D коэффициенты в А и В формах записи.
Задача 2.7.9 Известны сопротивления холостого хода и короткого замыкания симметричного ЧП: 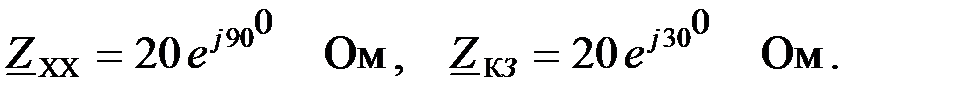 Определить коэффициенты всех форм записи уравнений ЧП: А, В, Z, Y, G, H.
Определить коэффициенты всех форм записи уравнений ЧП: А, В, Z, Y, G, H.
Задача 2.7.10 Для симметричного ЧП приборы электромагнитных и электродинамических систем показали следующие значения:


Определить коэффициенты А – формы записи уравнений ЧП. Определить сопротивления ветвей ЧП и построить Т и П – образные схемы замещения.
Задача 2.7.11 Для несимметричного ЧП в режиме холостого хода и короткого замыкания приборы показали следующие значения: 

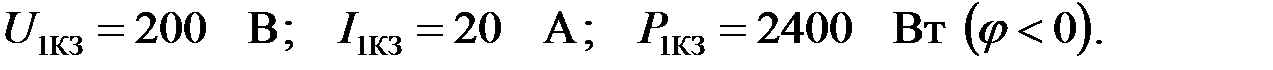


Определить коэффициенты А, B, Z, Y – форм записи.
Задача 2.7.12 Известны 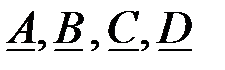 коэффициенты A формы записи уравнений ЧП:
коэффициенты A формы записи уравнений ЧП:  Определить сопротивления ветвей и построить Т и П – образные схемы замещения.
Определить сопротивления ветвей и построить Т и П – образные схемы замещения.
Задача 2.7.13 Известны сопротивления Т – образной схемы замещения ЧП: 
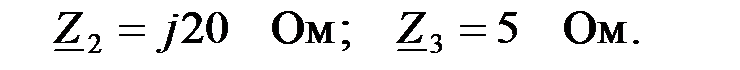 Определить коэффициенты А, B, Z, Y – форм записи.
Определить коэффициенты А, B, Z, Y – форм записи.
Задача 2.7.14 Известны сопротивления П – образной схемы замещения  Определить коэффициенты А, B, Z, Y – форм записи.
Определить коэффициенты А, B, Z, Y – форм записи.
Задача 2.7.15 Известны А, В, С, D коэффициенты A – формы записи уравнений симметричного ЧП:  Определить характеристические параметры четырехполюсника.
Определить характеристические параметры четырехполюсника.
Задача 2.7.16 У несимметричного ЧП известны сопротивления холостого хода и короткого замыкания: 


 Определить
Определить  коэффициенты и характеристические параметры ЧП.
коэффициенты и характеристические параметры ЧП.
Задача 2.7.17 Два одинаковых четырехполюсника, схема одного из них показана на рис.2.7.17 с параметрами  соединены каскадно. Определить соединены каскадно. Определить  – коэффициенты сложного ЧП. – коэффициенты сложного ЧП.
|
Задача 2.7.18 Два одинаковых четырехполюсника, схема одного из них показана на рис.2.7.17 с параметрами  соединены последовательно. Определить Z – параметры сложного ЧП.
соединены последовательно. Определить Z – параметры сложного ЧП.
Задача 2.7.19Два одинаковых ЧП, показанных на рис.2.7.19 с параметрами  соединены параллельно. Определить Y – параметры сложного ЧП. соединены параллельно. Определить Y – параметры сложного ЧП.
| |||
Задача 2.7.20 Для активного ЧП, представленного на рис.2.7.20, найти  – коэффициенты ЧП и записать расчетные уравнения для определения – коэффициенты ЧП и записать расчетные уравнения для определения  и и 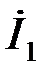 в А – форме, если заданы следующие параметры: в А – форме, если заданы следующие параметры:  
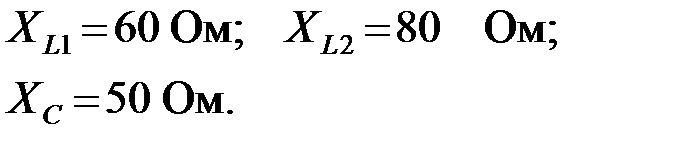
| |||
Задача 2.7.21Для ЧП, представленного на рис.2.7.21 построить круговую диаграмму для тока 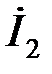 , если , если 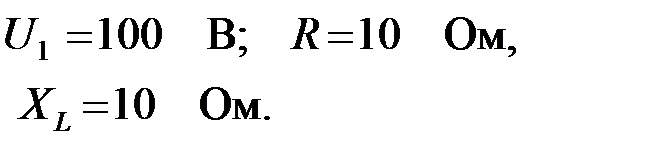
| |||
Задача 2.7.22Для ЧП, представленного на рис.2.7.22 построить круговую диаграмму для тока  , если , если  Нагрузка носит индуктивный характер.
Нагрузка носит индуктивный характер.
| |
Задача 2.7.23 Для ЧП, представленного на рис.2.7.23, построить круговые диаграммы для токов   и и  ,
если: ,
если:    характер нагрузки – емкостной. характер нагрузки – емкостной.
| |
Задача 2.7.24Для ЧП представленного на рисунке 2.7.24 заданы следующие параметры:   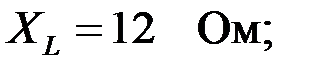   Ом. Ом.
|
Определить  коэффициенты и записать уравнение в А
коэффициенты и записать уравнение в А  форме, вычислить сопротивления холостого хода и короткого замыкания и построить Т и П
форме, вычислить сопротивления холостого хода и короткого замыкания и построить Т и П  образные схемы замещения ЧП. Найти характеристические параметры
образные схемы замещения ЧП. Найти характеристические параметры  . Построить круговую диаграмму для тока
. Построить круговую диаграмму для тока  , при изменении по модулю сопротивления нагрузки
, при изменении по модулю сопротивления нагрузки 
Дата добавления: 2015-10-21; просмотров: 147 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Это значение полностью совпадает с напряжением на векторной диаграмме. | | | ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ 1 страница |