
Читайте также:
|
3.1 Фильтры низкой частоты типа «k»
Задача 3.1.1 Подобрать емкость фильтра низкой частоты (ФНЧ), собранного по П – схеме, чтобы получить частоту среза 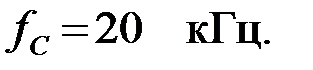 Индуктивность фильтра
Индуктивность фильтра  Вычислить коэффициент фазы и характеристическое сопротивление на частоте
Вычислить коэффициент фазы и характеристическое сопротивление на частоте  .
.
Решение
Найдем номинальное волновое сопротивление  , используя частоту среза и индуктивность: , используя частоту среза и индуктивность:
 
|
Тогда ёмкость фильтра:

Характеристическое сопротивление ФНЧ в полосе пропускания носит активный характер и на частоте 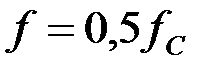 будет равно:
будет равно: 
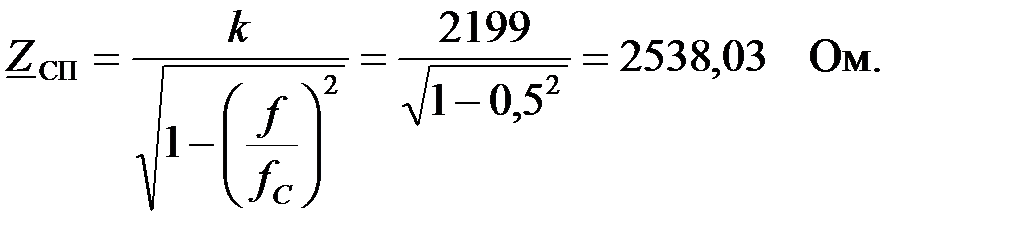
Коэффициент фазы 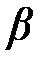 на частоте
на частоте 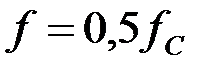 , можно определить следующим образом:
, можно определить следующим образом:

Задача 3.1.2 Определить полосу пропускания ФНЧ, собранного по Т – схеме и вычислить характеристические сопротивления на частотах 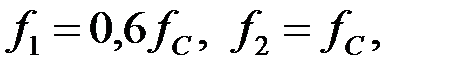
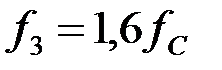
если параметры фильтра равны: 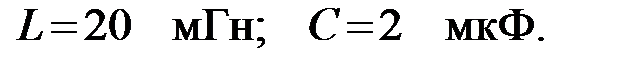
Решение
ФНЧ пропускает сигналы в полосе пропускания от нуля до частоты среза.
Определим частоту среза:
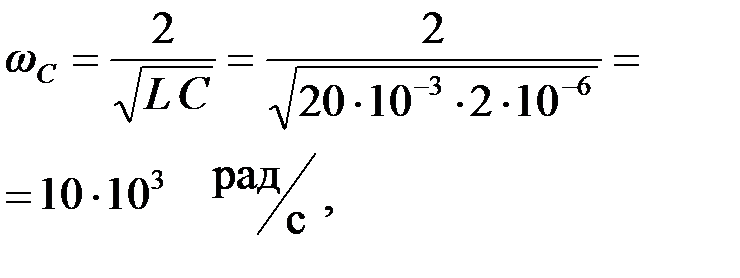 или
или 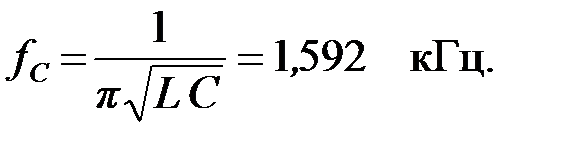
|
Характеристическое сопротивление ФНЧ, собранного по Т – образной схеме можно найти из выражения: 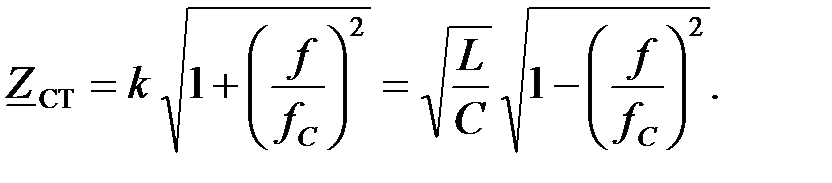
На частоте  в полосе пропускания характеристическое сопротивление носит активный характер:
в полосе пропускания характеристическое сопротивление носит активный характер:

На частоте 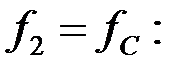
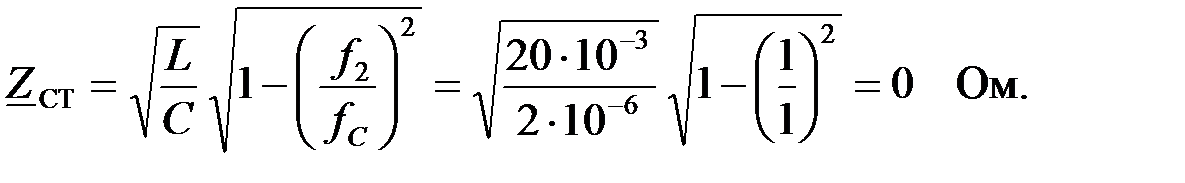
На частоте 
 в полосе затухания характеристическое сопротивление носит индуктивный характер:
в полосе затухания характеристическое сопротивление носит индуктивный характер: 
Задача 3.1.3. Характеристическое сопротивление фильтра низкой частоты 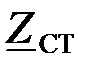 , собранного по Т – образной схеме на частоте
, собранного по Т – образной схеме на частоте 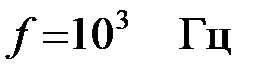 равно 120 Ом, а частота среза
равно 120 Ом, а частота среза  Определить параметры фильтра.
Определить параметры фильтра.
Решение
Используя заданное характеристическое сопротивление  можно определить номинальное волновое сопротивление можно определить номинальное волновое сопротивление  : :

|
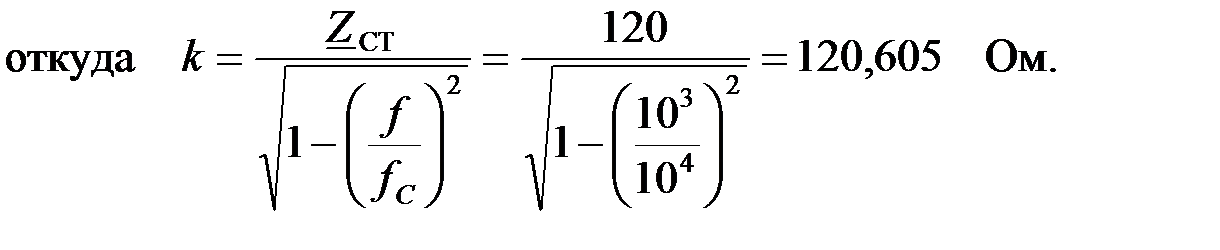
Зная частоту среза и номинальное волновое сопротивление  , найдем
, найдем  параметры фильтра:
параметры фильтра: 
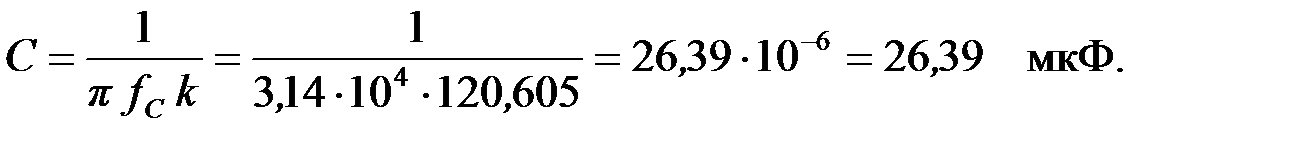
Задача 3.1.4 Определить индуктивность ФНЧ, собранного по Т – образной схеме (рис.3.1.4,а). Рассчитать характеристические сопротивления на частотах: 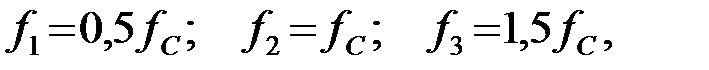 если известно что:
если известно что: 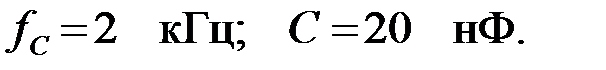 Построить векторную диаграмму фильтра на частоте –
Построить векторную диаграмму фильтра на частоте – 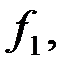 если действующее значение входного напряжения равно 50 В.
если действующее значение входного напряжения равно 50 В.
Решение
Т.к. заданы частота среза и емкость фильтра, определим его индуктивность:
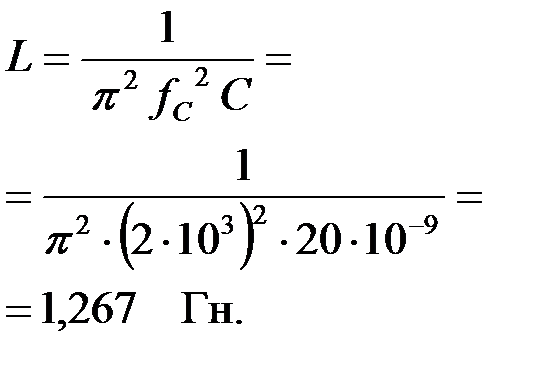
|
Вычислим характеристические сопротивления на частотах 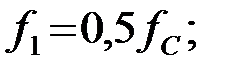
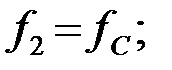

1) Для частоты 

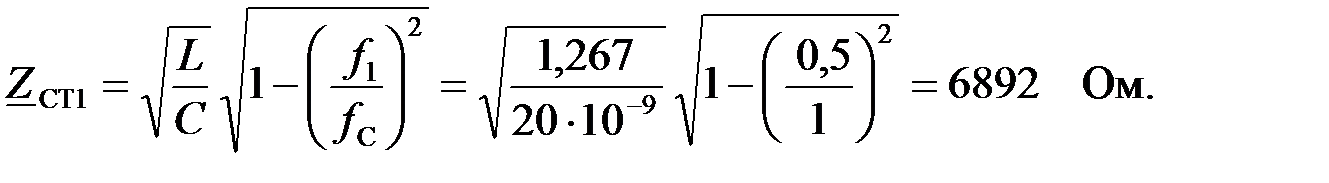
2)  Для частоты
Для частоты 

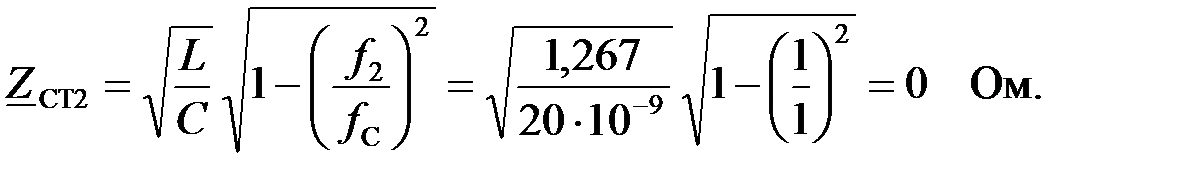
3) Для частоты 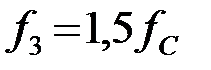 :
:
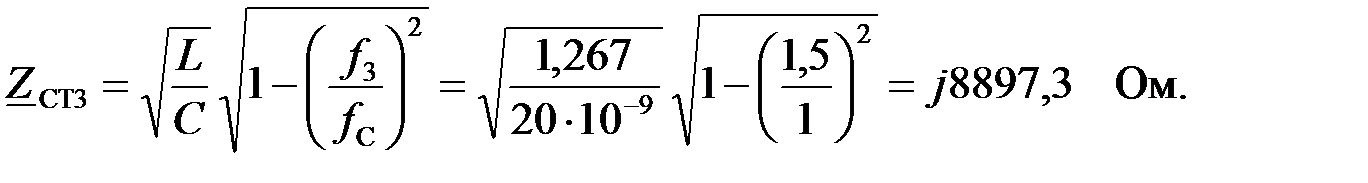
Проведем расчет токов и напряжений для частоты 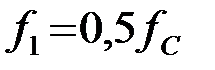 . Схема замещения фильтра показана на рис.3.1.4.б. Найдем вначале сопротивления . Схема замещения фильтра показана на рис.3.1.4.б. Найдем вначале сопротивления  и и  : :

|
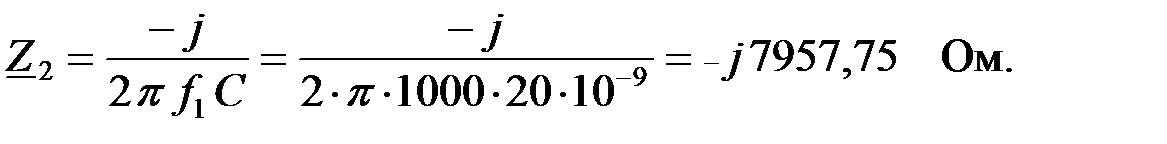
Затем найдем токи в ветвях:


Зная токи и сопротивления найдем напряжение на выходе ФНЧ:
 Векторная диаграмма токов и напряжения ФНЧ приведена на рис.3.1.4,в. Векторная диаграмма токов и напряжения ФНЧ приведена на рис.3.1.4,в.
|
Задача 3.1.5 Найти сопротивления холостого хода и короткого замыкания фильтра, представленного на рис. 3.1.5,а на частоте 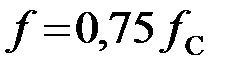 , если
, если 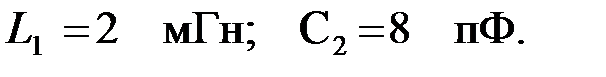 Определить характеристическое сопротивление фильтра на указанной частоте и граничные частоты, при которых характеристическое сопротивление остается вещественным, а также чему равен коэффициент затухания на частоте:
Определить характеристическое сопротивление фильтра на указанной частоте и граничные частоты, при которых характеристическое сопротивление остается вещественным, а также чему равен коэффициент затухания на частоте: 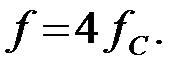 Построить графические зависимости
Построить графические зависимости 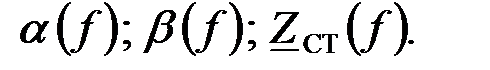
Решение
Вычислим частоту среза:
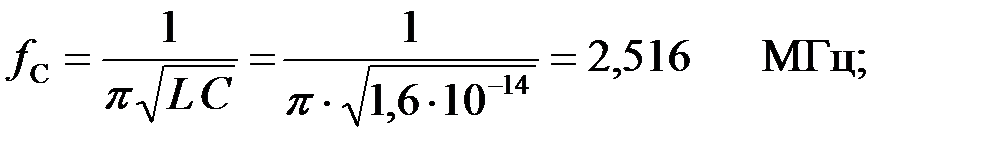 Найдём текущую частоту сигнала из равенства
Найдём текущую частоту сигнала из равенства 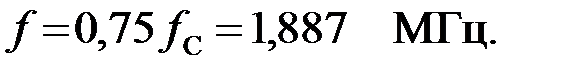
|
Определим сопротивления  и
и 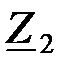 на заданной частоте:
на заданной частоте:
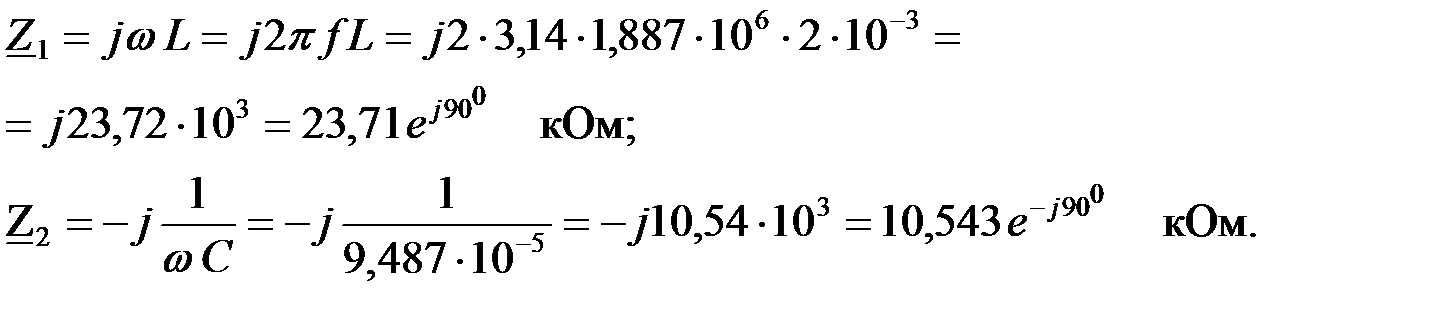
Вычислим сопротивление холостого хода и короткого замыкания:
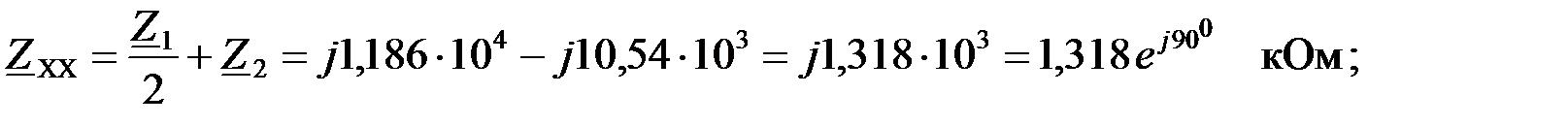
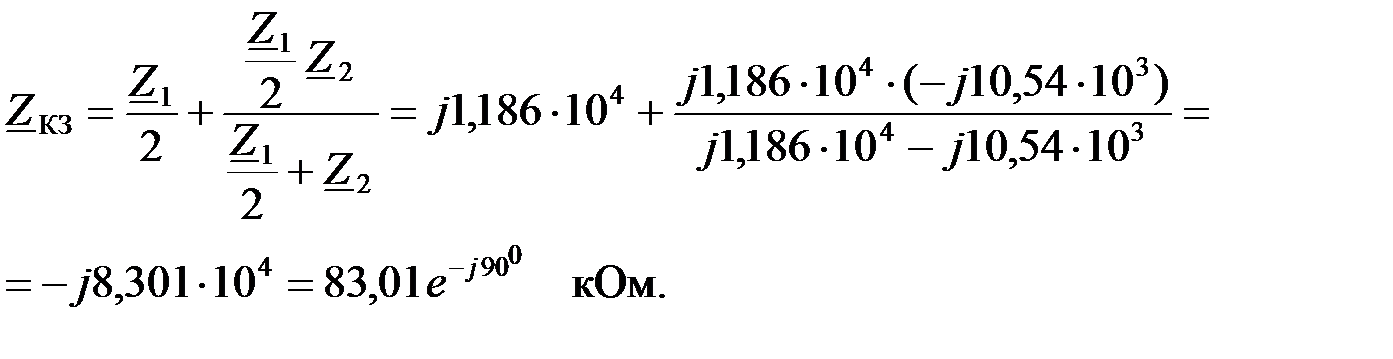
Найдем характеристическое сопротивление 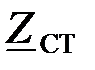 :
:
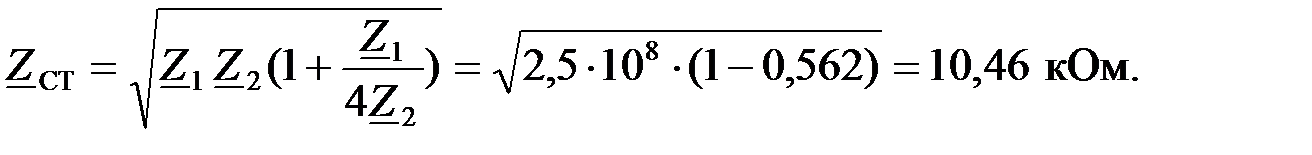
Определим коэффициент затухания «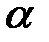 » на частоте
» на частоте 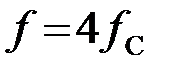 :
: 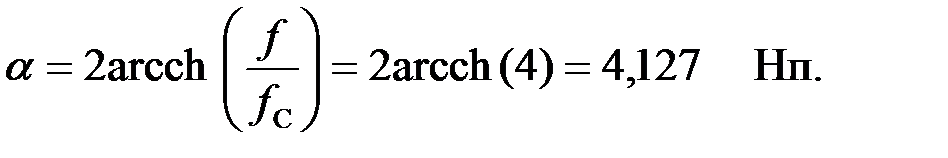
На рис. 3.1.5,б, в, г приведены графики изменения 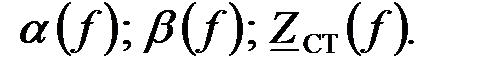
Задача 3.1.6 Заданы параметры фильтра низкой частоты, собранного по Т – образной схеме:  Определить характеристическое сопротивление
Определить характеристическое сопротивление 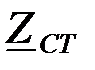 и меру передачи
и меру передачи  на частоте
на частоте 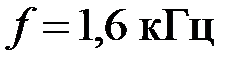 . Построить векторную диаграмму токов и падений напряжений для заданного фильтра.
. Построить векторную диаграмму токов и падений напряжений для заданного фильтра.
Решение
Схема фильтра показана на рис.3.1.6,а. Определим частоту среза:
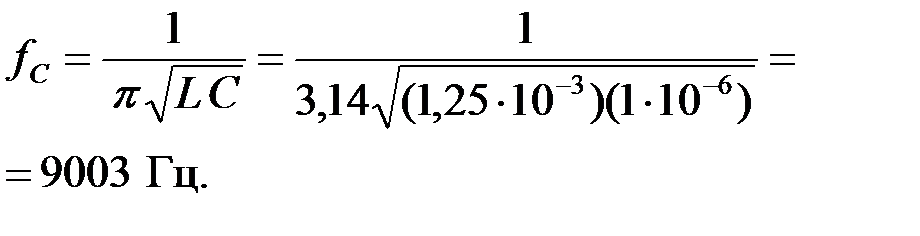
|
Используя частоту среза и индуктивность, найдем вначале номинальное волновое сопротивление 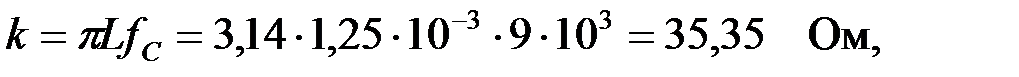
а затем найдем характеристическое сопротивление Т – образногoфильтра:
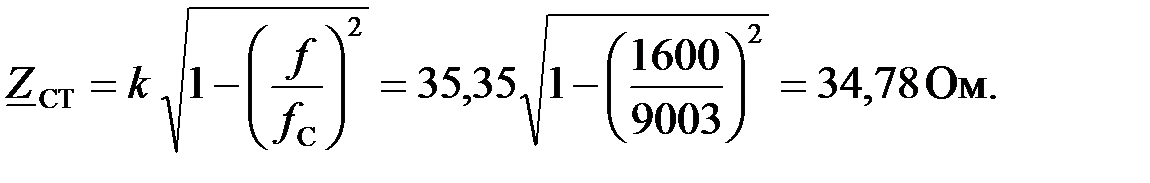
Т.к. частота сигнала находится в полосе пропускания коэффициент затухания 
Это значит, что мера передачи  будет определяться коэффициентом фазы «
будет определяться коэффициентом фазы «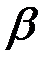 », который можно найти следующим образом:
», который можно найти следующим образом:

Схема замещения фильтра показана на рис.3.1.6,б.
Найдем сопротивления 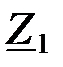 и и 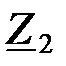 : :
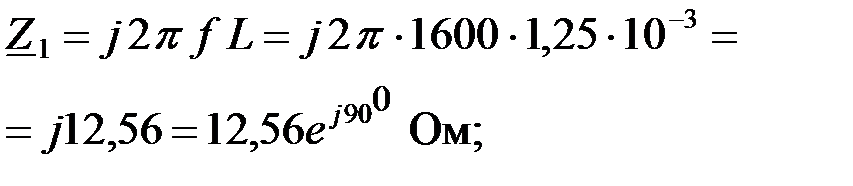 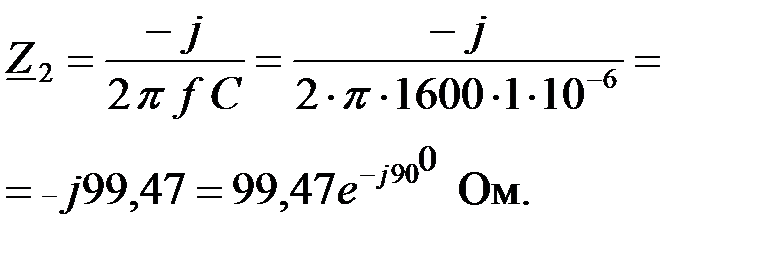
| |||
Рассчитаем токи в ветвях и напряжения на элементах ФНЧ.
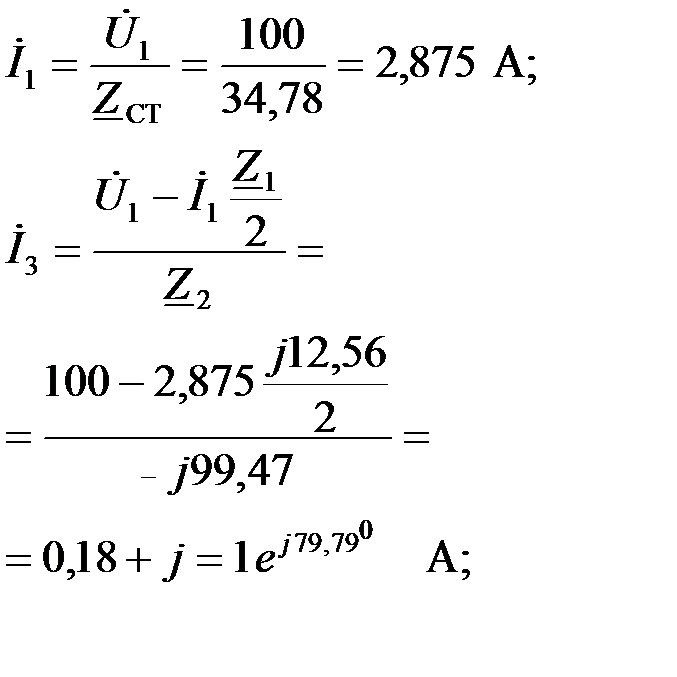
| |||



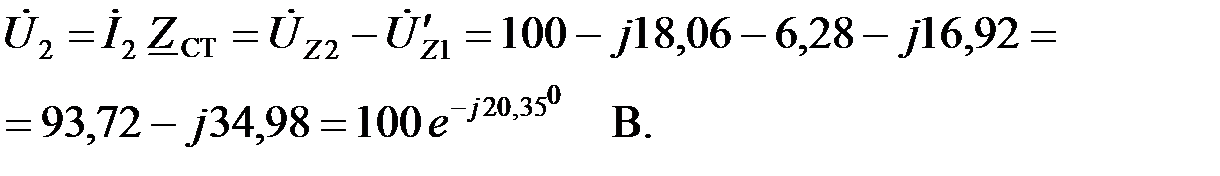
Векторная диаграмма токов и нгапряжений приведена на рис.3.1.6,в.
Задача 3.1.7 ФНЧ собран по П–схеме (рис.3.1.7,а). Известны параметры фильтра:  На входные зажимы фильтра подано напряжение
На входные зажимы фильтра подано напряжение 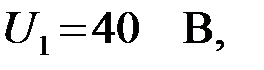 на частоте
на частоте  На выходные зажимы включено сопротивление, согласованное с фильтром. Определить характеристическое сопротивление фильтра и коэффициент фазы, а также рассчитать все токи и напряжения в схеме, на заданной частоте и построить векторную диаграмму токов и напряжений.
На выходные зажимы включено сопротивление, согласованное с фильтром. Определить характеристическое сопротивление фильтра и коэффициент фазы, а также рассчитать все токи и напряжения в схеме, на заданной частоте и построить векторную диаграмму токов и напряжений.
Решение
Определим частоту среза ФНЧ:

|
Фильтр находится в полосе пропускания и его характеристическое сопротивление носит активный характер и определяется следующим образом:
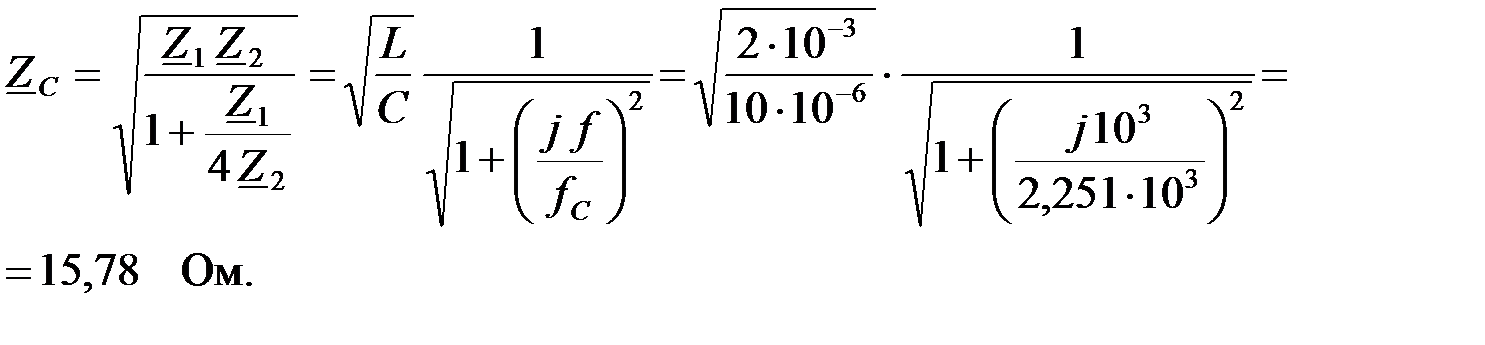
Коэффициент фазы 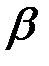 на заданной частоте:
на заданной частоте:

Для определения токов и построения векторной диаграммы, рассчитаем сопротивления фильтра на заданной частоте:
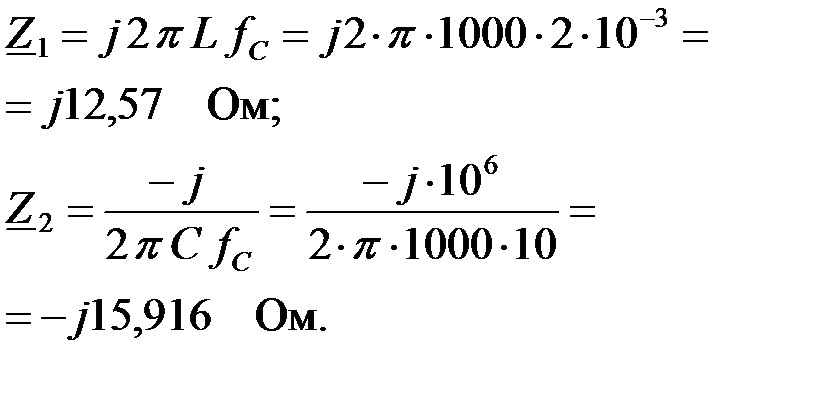
|
Определим токи и напряжения фильтра (рис.3.1.7,б) на заданной частоте:

|
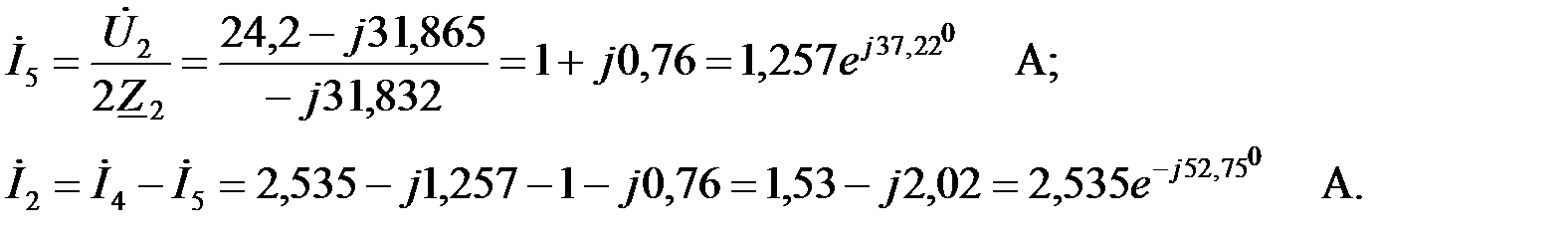 Векторная диаграмма токов и напряжений приведена на рис.3.1.7, в.
Векторная диаграмма токов и напряжений приведена на рис.3.1.7, в.
Задача 3.1.8 У ФНЧ, представленного на рис. 3.1.8,а, известны следующие параметры: k = 500 Ом; 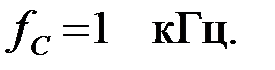 Определить
Определить 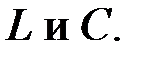 параметры фильтра. Рассчитать токи и напряжения в схеме, если фильтр работает на частоте
параметры фильтра. Рассчитать токи и напряжения в схеме, если фильтр работает на частоте 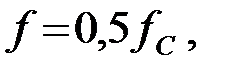 а действующее значение тока на выходе фильтра
а действующее значение тока на выходе фильтра 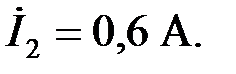 Построить векторную диаграмму токов и напряжений, а также и зависимости коэффициента затухания и характеристического сопротивления от частоты.
Построить векторную диаграмму токов и напряжений, а также и зависимости коэффициента затухания и характеристического сопротивления от частоты.
| Решение Зная частоту среза и номинальное волновое сопротивление определим параметры фильтра: |
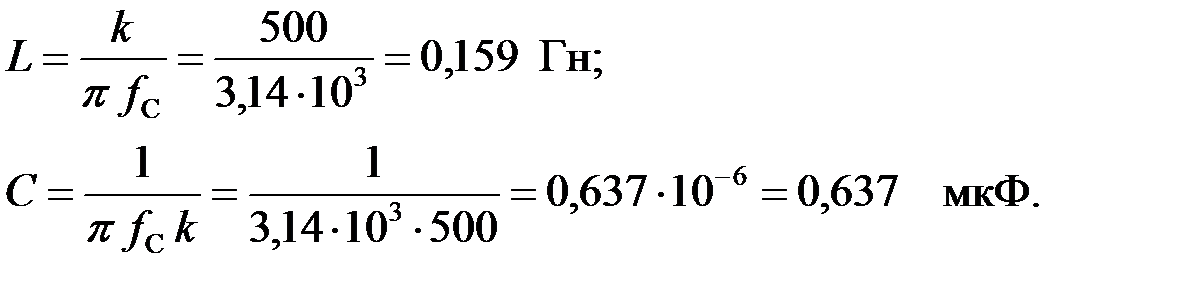
Фильтр находится в полосе пропускания, его характеристическое сопротивление имеет активный характер и определяется следующим образом:
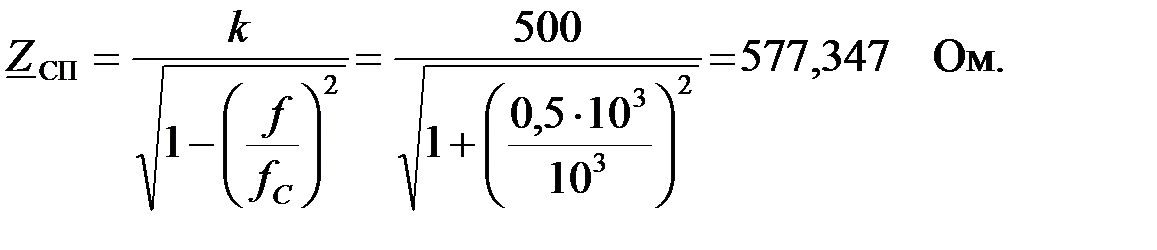
Для определения токов и построения векторной диаграммы, рассчитаем сопротивления фильтра на частоте  :
:
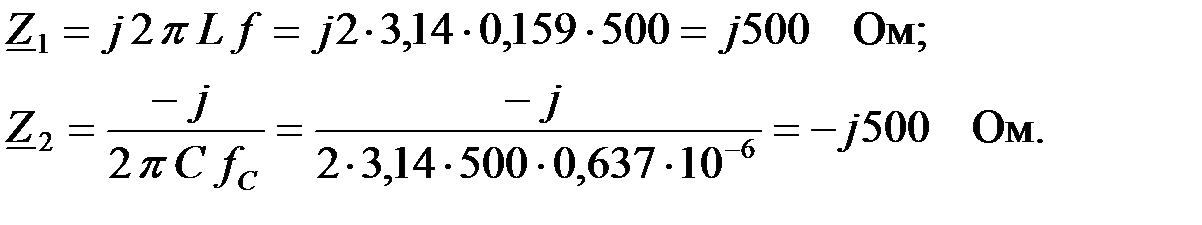
Определим токи и напряжения фильтра (рис.3.1.8,б) на заданной частоте:
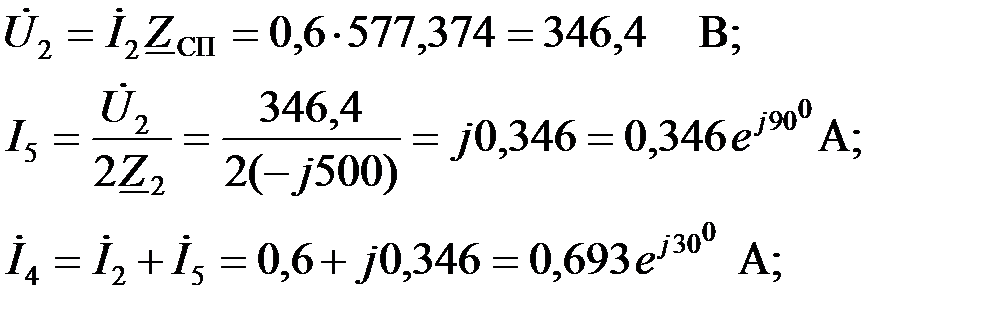
|
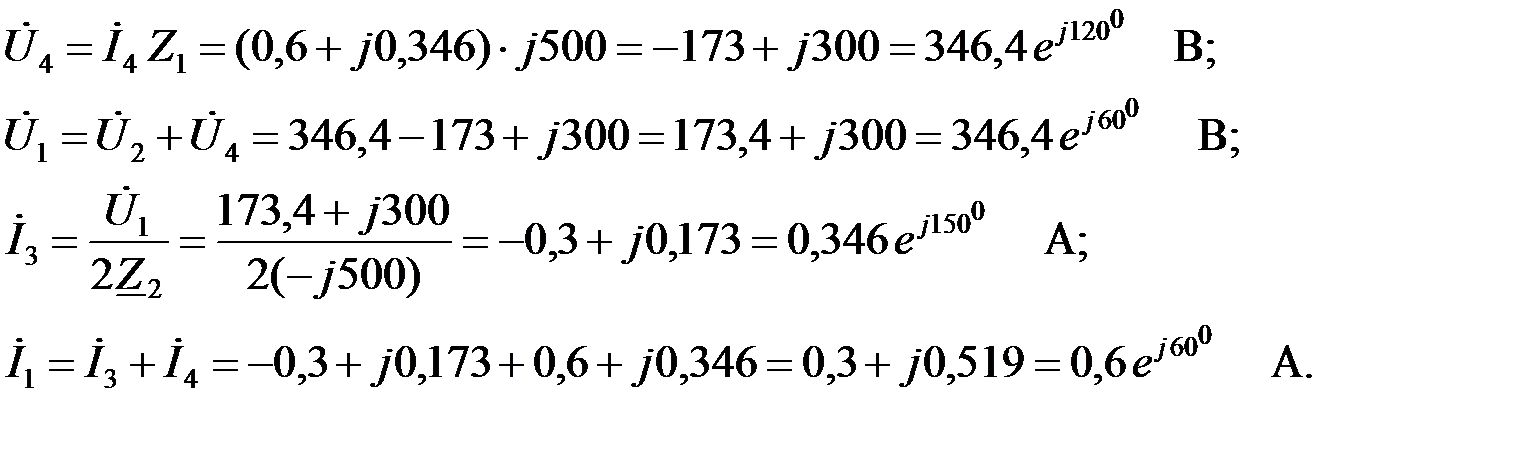
|
Векторная диаграмма токов и напряжений показана на рис 3.1.8,в.
На рис. 3.1.8, г, д приведены графики изменения  Коэффициент затухания изменяется по закону:
Коэффициент затухания изменяется по закону:
| |||
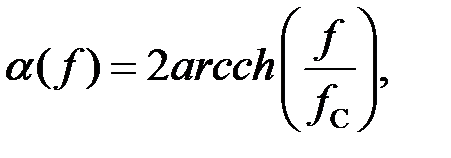 а характеристическое сопротивление по закону:
а характеристическое сопротивление по закону:
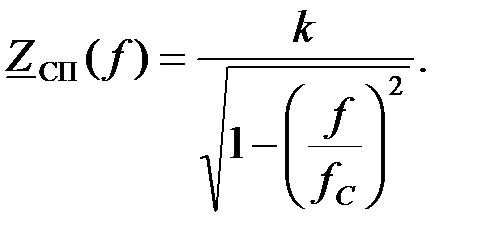
| |||
Задача 3.1.9 ФНЧ собран по «П» схеме, представленной на рис.3.1.9,а. Известны параметры элементов фильтра: 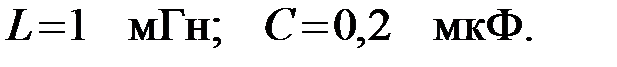 На входные зажимы фильтра «mn» подано напряжение
На входные зажимы фильтра «mn» подано напряжение 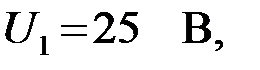 на частоте
на частоте 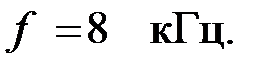 На выходные зажимы «pq» включено сопротивление, согласованное с фильтром. Требуется определить характеристическое сопротивление фильтра и меру передачи. Построить графические зависимости коэффициента фазы и характеристического сопротивления в функции частоты.
На выходные зажимы «pq» включено сопротивление, согласованное с фильтром. Требуется определить характеристическое сопротивление фильтра и меру передачи. Построить графические зависимости коэффициента фазы и характеристического сопротивления в функции частоты.
| Решение Характеристическое сопротивление П – образного фильтра можно определить через сопротивления холостого хода и короткого замыкания или через сопротивления звеньев фильтра. |
Для примера покажем различные способы.
Определим характеристическое сопротивление по сопротивлениям 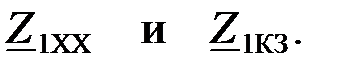
Для того, чтобы определить характеристическое сопротивление
k через параметры элементов фильтра на заданной частоте, вычислим
вначале частоту среза:
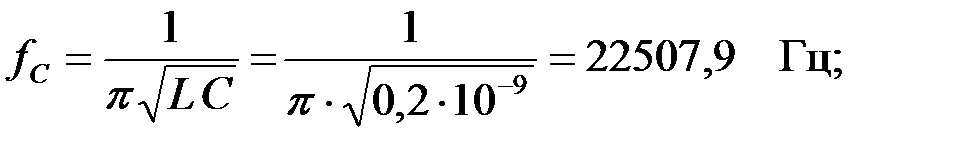
Тогда 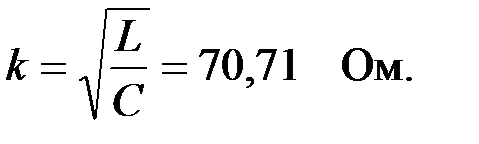
откуда характеристическое сопротивление П – образного ФНЧ:
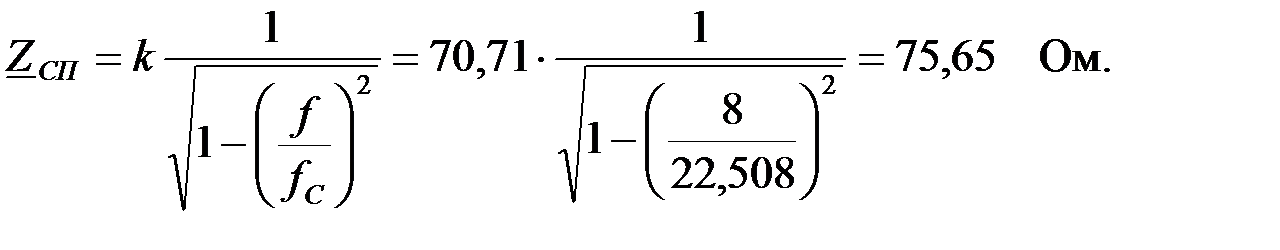
Рабочая частота  соответствует полосе пропускания фильтра, следовательно, коэффициент затухания «
соответствует полосе пропускания фильтра, следовательно, коэффициент затухания «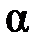 » равен нулю. Мера передачи
» равен нулю. Мера передачи  будет определяться коэффициентом фазы, который можно определить, следующим образом:
будет определяться коэффициентом фазы, который можно определить, следующим образом:

тогда 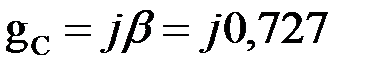
На рис. 3.1.9, б, в приведены графики

3.2 Фильтры высокой частоты типа «k»
Задача 3.2.1 Подобрать индуктивность фильтра высокой частоты (ФВЧ), собранного по Т – образной схеме, если частота среза 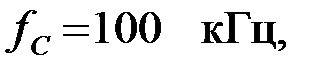 а емкость фильтра
а емкость фильтра  Определить характеристическое сопротивление фильтра
Определить характеристическое сопротивление фильтра  на частоте
на частоте 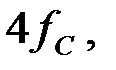 и построить зависимость характеристического сопротивления в функции частоты
и построить зависимость характеристического сопротивления в функции частоты  .
. 
|
| Решение
Схема ФВЧ приведена на рис.3.2.1,а.
Зная частоту среза фильтра и его емкость элементов, определим индуктивность, используя выражение:
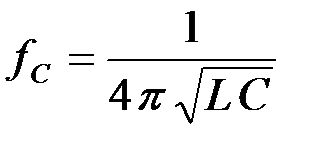 , тогда , тогда
|

Вычислим характеристическое сопротивление фильтра на частоте 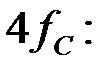
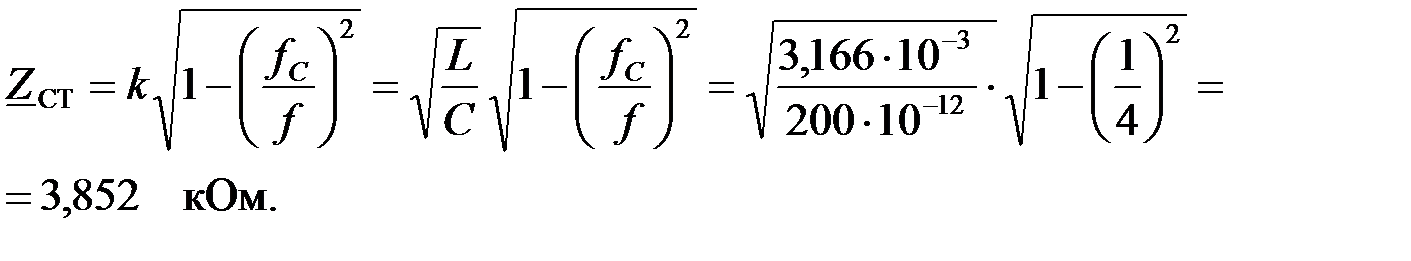
Зависимость характеристического сопротивления от частоты определяется выражением:

Анализ графической зависимости 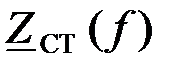 приведенной на рис.3.2.1,б, показывает, что при прохождении частоты среза приведенной на рис.3.2.1,б, показывает, что при прохождении частоты среза 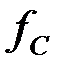 у характеристического сопротивления меняется реакция с емкостной на активную. у характеристического сопротивления меняется реакция с емкостной на активную.
|
Задача 3.2.2 Определить параметры  элементов ФВЧ (рис.3.2.2), если характеристическое сопротивление фильтра на угловой частоте
элементов ФВЧ (рис.3.2.2), если характеристическое сопротивление фильтра на угловой частоте  равно 50 Ом, а угловая частота среза
равно 50 Ом, а угловая частота среза 
Решение
Через характеристическое сопротивление 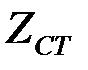 и частоту и частоту 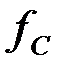 среза определим номинальное характеристическое сопротивление k: среза определим номинальное характеристическое сопротивление k:
|

откуда 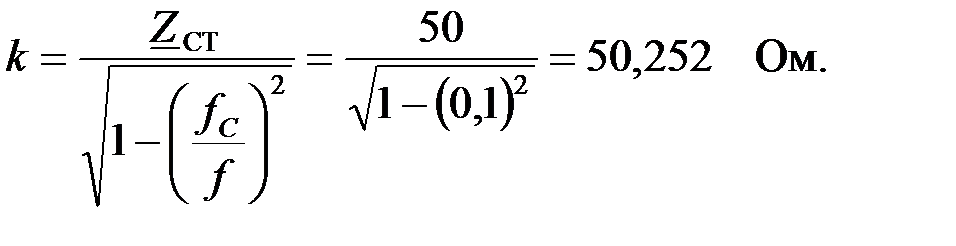
Зная k найдем  параметры элементов ФВЧ:
параметры элементов ФВЧ:


Задача 3.2.3 Определить частоту среза фильтра высокой частоты, собранного по П – схеме и характеристические сопротивления на частотах 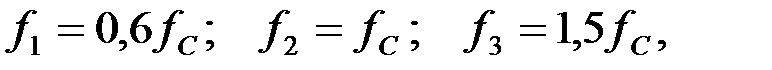 если его параметры звеньев известны и равны:
если его параметры звеньев известны и равны: 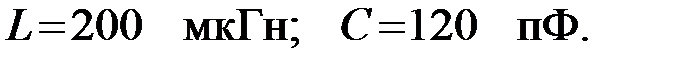 Построить графическую зависимость
Построить графическую зависимость 
| Решение Схема ФВЧ, собранного по П – схеме показана на рис.3.2.3,а. Определим частоту среза ФВЧ: |

Вычислим характеристические сопротивления на частотах: 
В общем случае характеристическое сопротивление ФВЧ, собранного по П – образной схеме определяется выражением:
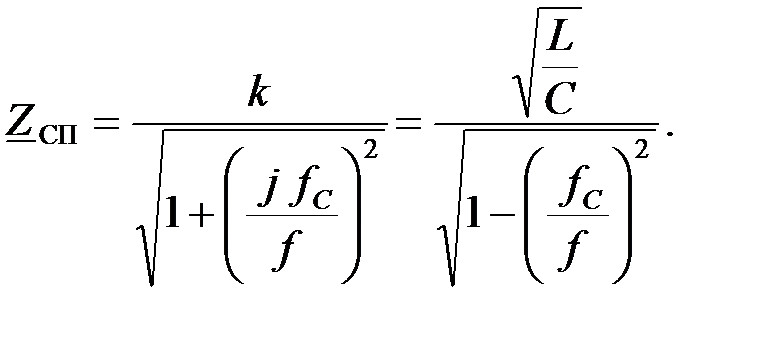

На частоте 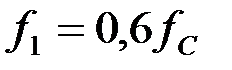 в полосе затухания характеристическое сопротивление носит индуктивный характер:
в полосе затухания характеристическое сопротивление носит индуктивный характер:
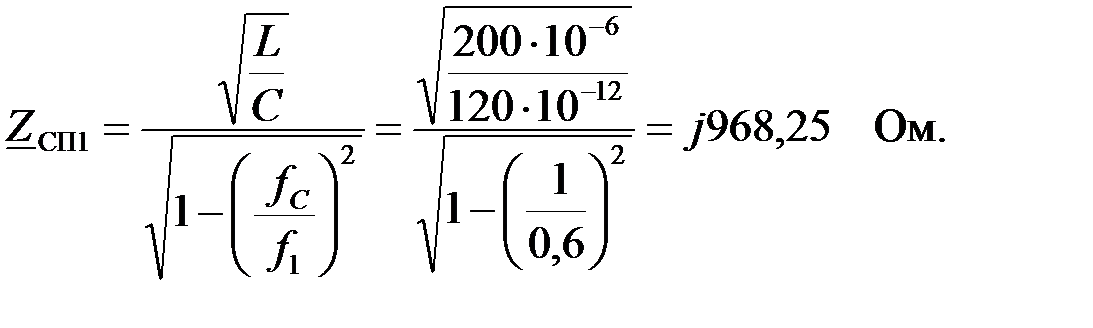
На частоте 
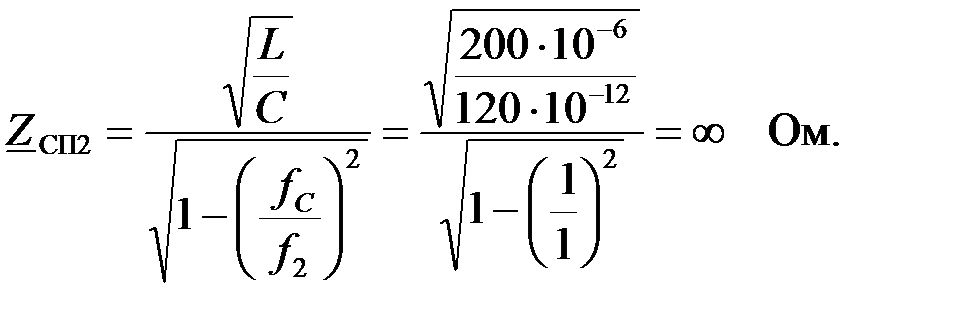
Дата добавления: 2015-10-21; просмотров: 381 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи смешанного типа | | | ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ 2 страница |