
Читайте также:
|
На частоте 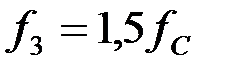
 в полосе прозрачности характеристическое сопротивление носит активный характер:
в полосе прозрачности характеристическое сопротивление носит активный характер:
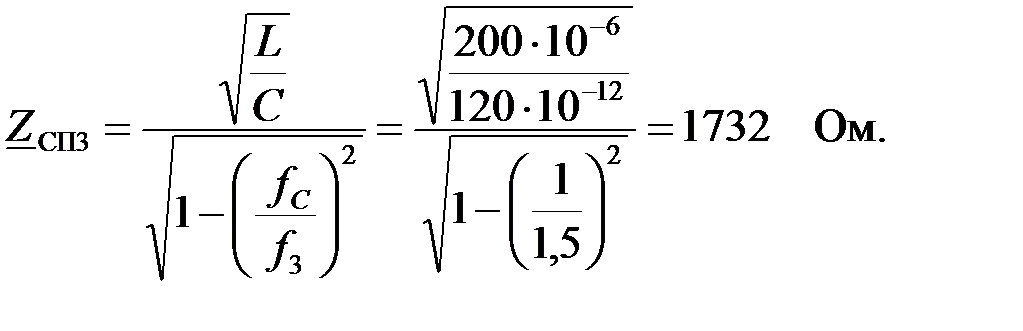
Для построения графической зависимости 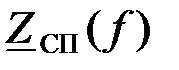 , вычислим несколько значений
, вычислим несколько значений 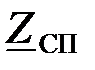 на разных частотах и сведем расчеты в таблицу:
на разных частотах и сведем расчеты в таблицу:
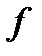
| 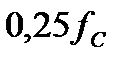
| 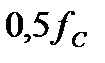
| 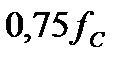
| 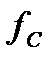
| 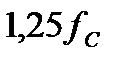
| 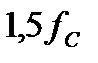
| 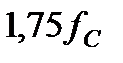
| 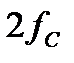
| 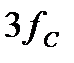
|
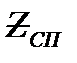 ,Ом ,Ом
| j 333,3 | j 745,36 | j 1464 | 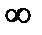
|
На рис. 3.2.3,б показан график изменения характеристического сопротивления П – образного фильтра ФВЧ от частоты, которое изменяется в соответствии с выражением:
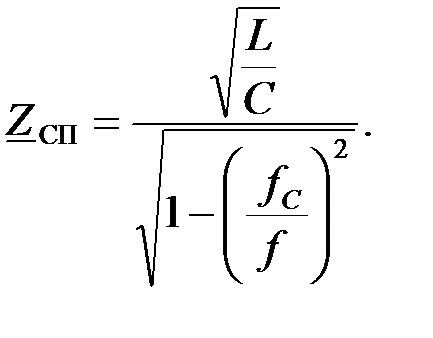
| ||
Рис.3.2.3,б
 Задача 3.2.4 У ФВЧ, собранного по Т – образной схеме, k = 200 Ом, а частота среза
Задача 3.2.4 У ФВЧ, собранного по Т – образной схеме, k = 200 Ом, а частота среза 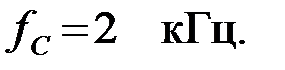 Определить
Определить  параметры фильтра. Рассчитать токи и напряжения в элементах схемы, если фильтр работает на частоте
параметры фильтра. Рассчитать токи и напряжения в элементах схемы, если фильтр работает на частоте 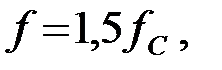 а действующее значение тока на входе –
а действующее значение тока на входе – 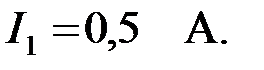 Построить векторную диаграмму токов и напряжений и зависимость характеристического сопротивления от частоты.
Построить векторную диаграмму токов и напряжений и зависимость характеристического сопротивления от частоты.
Решение
Схема фильтра ФВЧ приведена на рис,3.2.4,а.
Найдём рабочую частоту: 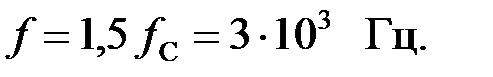 Определим параметры L – C элементов фильтра:
Определим параметры L – C элементов фильтра:
|
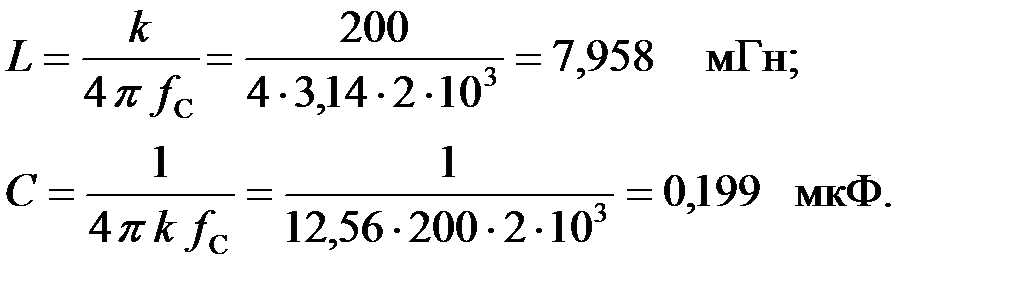
Вычислим комплексные сопротивления элементов фильтра при 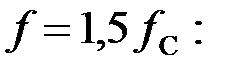 :
:

Найдем характеристическое сопротивление ФВЧ:
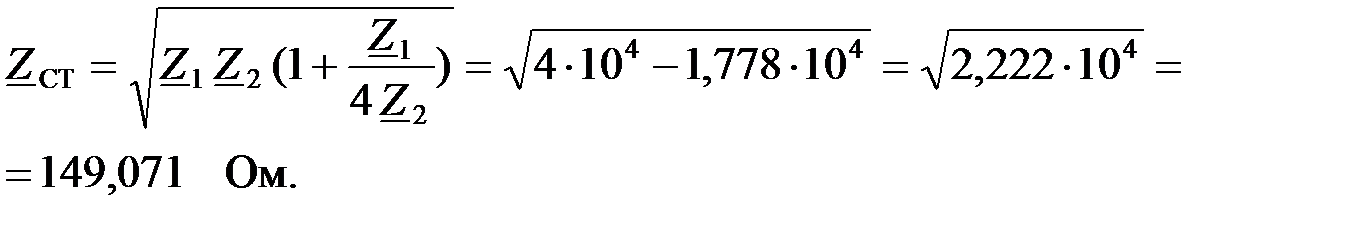
Проведем расчет токов и напряжений для заданной величины сигнала, используя характеристическое сопротивление  .
Схема замещения фильтра показана на рис.3.2.4,б. .
Схема замещения фильтра показана на рис.3.2.4,б.
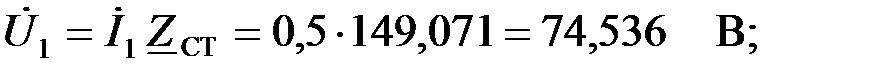
|
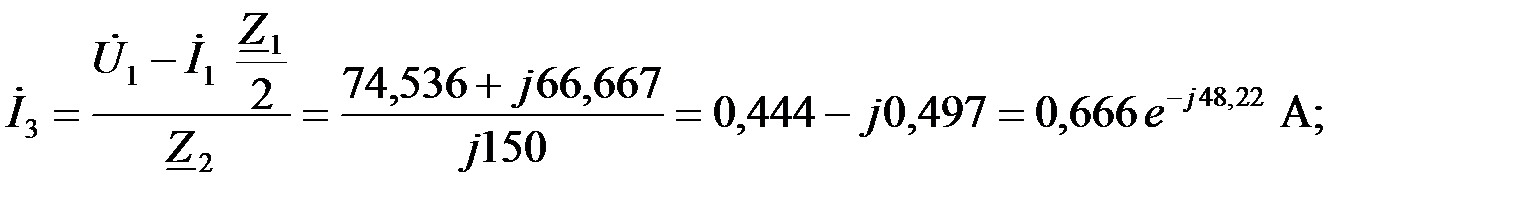
Найдем падения напряжений на последовательных звеньях ФВЧ:
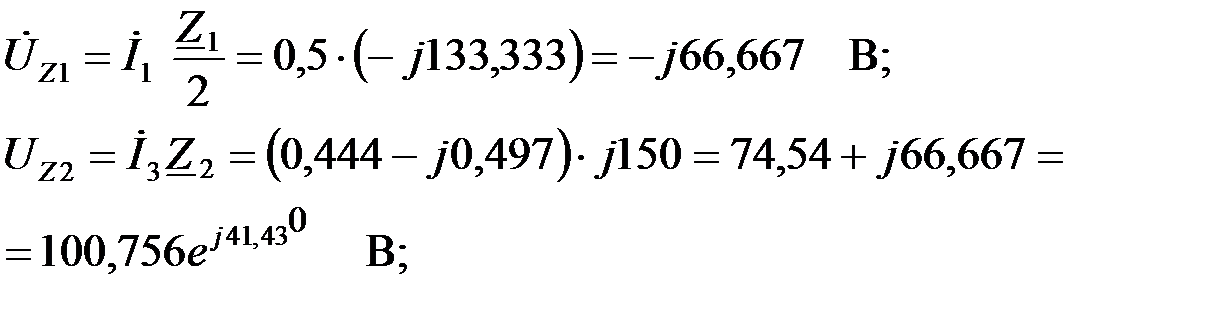
Определим ток на выходе ФВЧ:
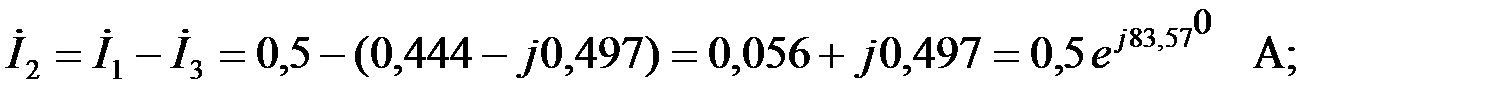
Тогда падение напряжения на последовательном выходном звене ФВЧ:
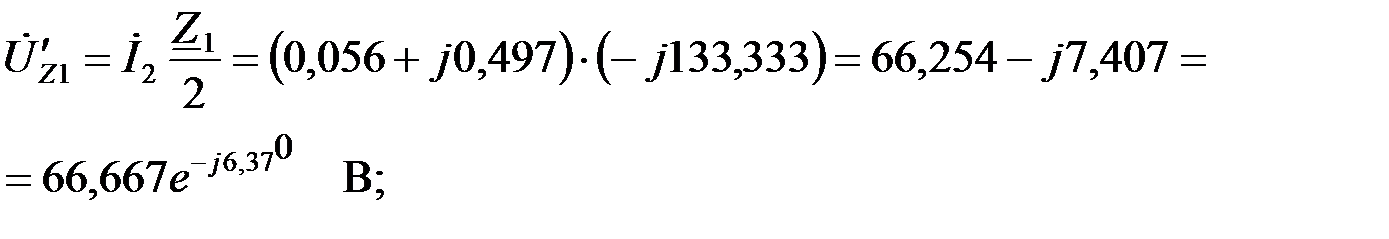
Найдем падение напряжения на параллельном звене ФВЧ:
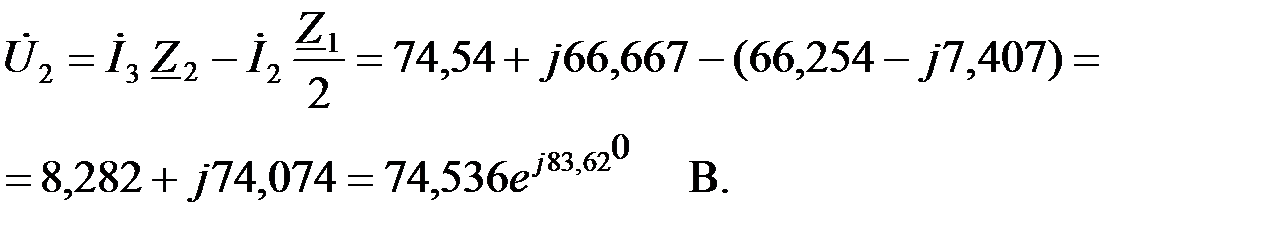
Векторная диаграмма токов и напряжений приведена на рис.3.2.4,в. На рис.3.2.4,г,д показаны графики изменения 
Задача 3.2.5 Определить токи и выходное напряжения фильтра, собранного по Т – образной схеме, если известно, что  Найти характеристическое сопротивление и меру передачи на заданной частоте. Рассчитать токи и напряжения в элементах фильтра. Построить зависимость коэффициента фазы от частоты.
Найти характеристическое сопротивление и меру передачи на заданной частоте. Рассчитать токи и напряжения в элементах фильтра. Построить зависимость коэффициента фазы от частоты.
Решение
Схема ФВЧ представлена на рис.3.2.5,а. Найдем номинальное волновое сопротивление фильтра:
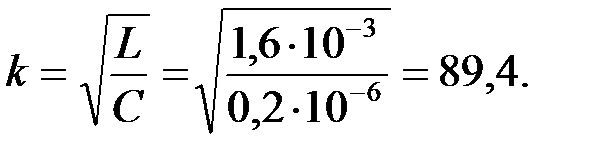
|
Определим частоту среза фильтра:
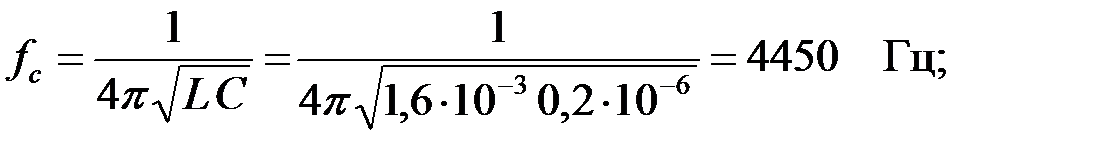
Характеристическое сопротивление фильтра на частоте 10 кГц найдем как:
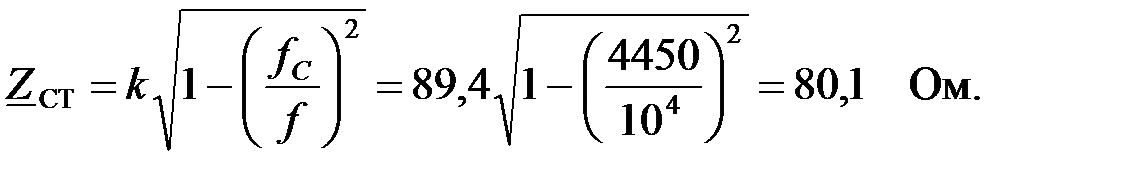
Расчитаем коэффициент фазы на заданной частоте:
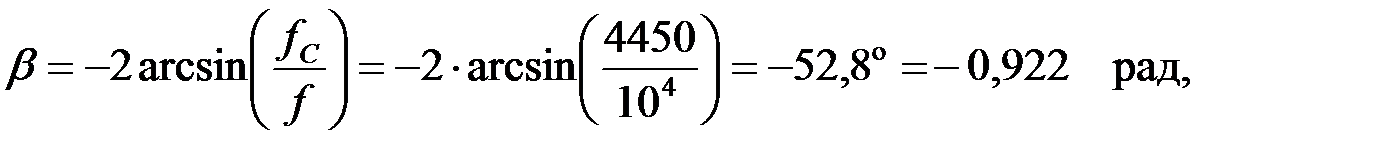
Так как рабочая частота принадлежит зоне прозрачности, то  , следовательно:
, следовательно:
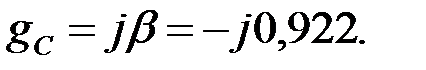
Для определения токов и напряжений в звеньях ФВЧ построим схему замещения фильтра (рис.3.2.5,б). Для этого рассчитаем сопротивления звеньев фильтра на заданной частоте  :
:
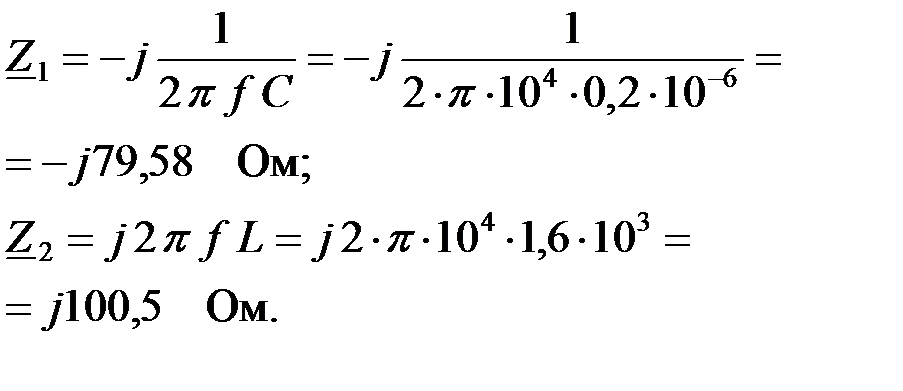 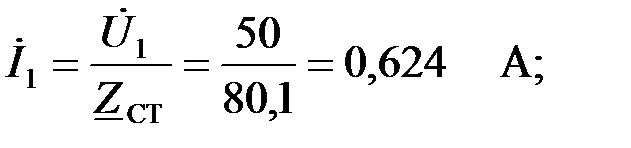
|
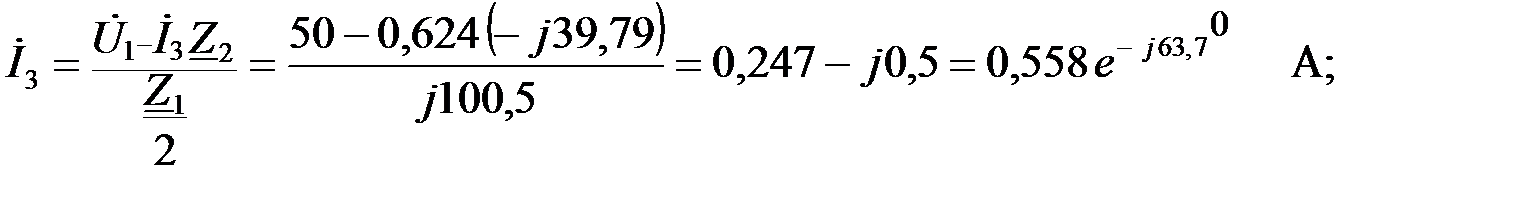
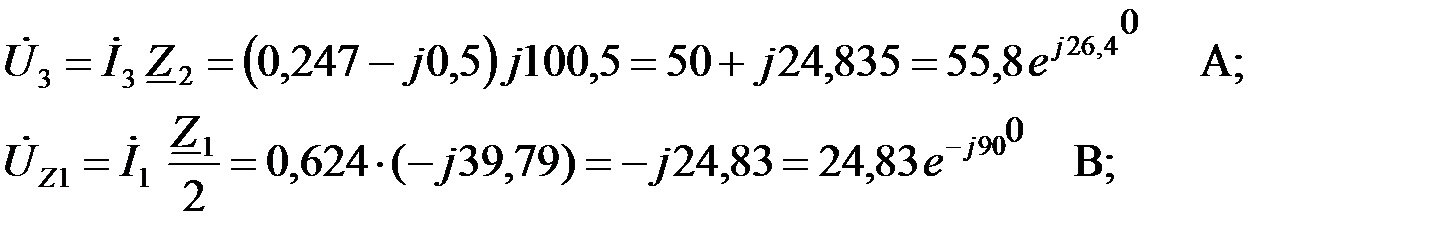
Ток в выходном звене ФВЧ находим в соответствии с первым законом Кирхгофа:
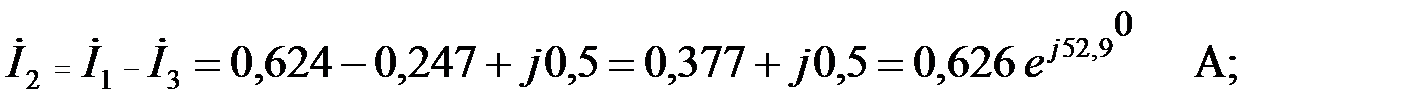
Тогда падение напряжений в выходном сопротивлении ФВЧ и на нагрузке:
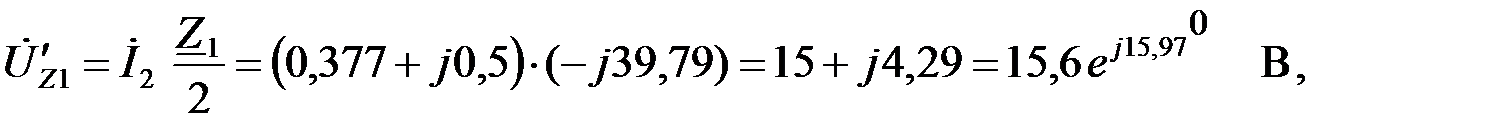
а напряжение на нагрузке:
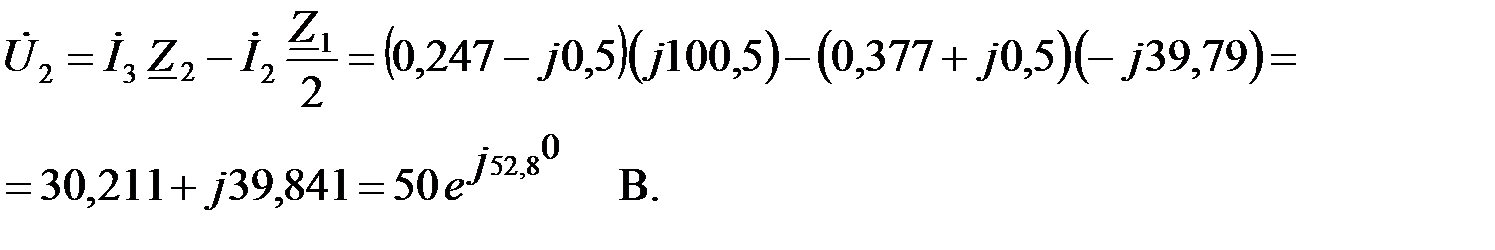
Зависимость коэффициента фазы 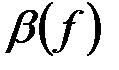 от частоты в полосе пропускания фильтра определяется соотношением:
от частоты в полосе пропускания фильтра определяется соотношением:
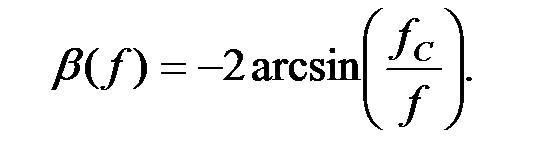
В полосе затухания коэффициент фазы равен:
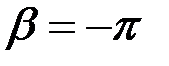 Зависимость
Зависимость 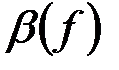 приведена на рис.3.2.5,в. приведена на рис.3.2.5,в.
|
Задача 3.2.6 Определить индуктивность ФВЧ, собранного по П – образной схеме, если известно, что 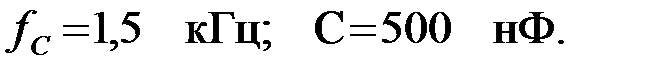 Рассчитать коэффициент затухания
Рассчитать коэффициент затухания 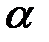 и характеристическое сопротивление
и характеристическое сопротивление 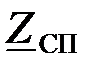 на частотах:
на частотах: 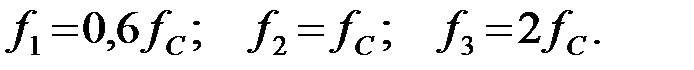 Построить векторную диаграмму токов и напряжений на частоте
Построить векторную диаграмму токов и напряжений на частоте 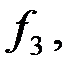 если действующее значение выходного напряжения
если действующее значение выходного напряжения 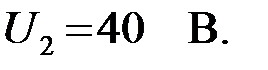
Решение
ФВЧ, собранный по П – образной схеме представлен на рис.3.2.6,а. Определим индуктивность ФВЧ используя частоту среза:

|
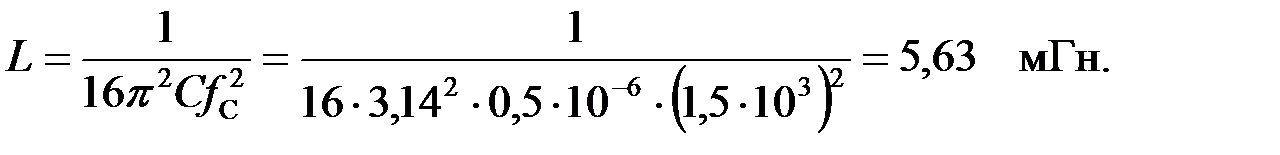
Находим коэффициент затухания на частоте: 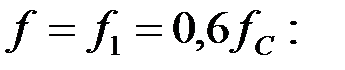
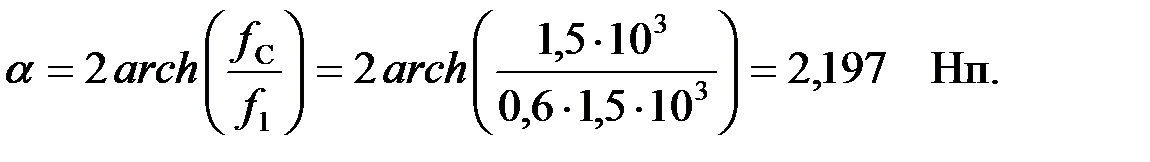
В полосе пропускания коэффициент затухания ФВЧ равен нулю.
Характеристическое сопротивление ФВЧ, собранного по П – образной схеме определяется как:
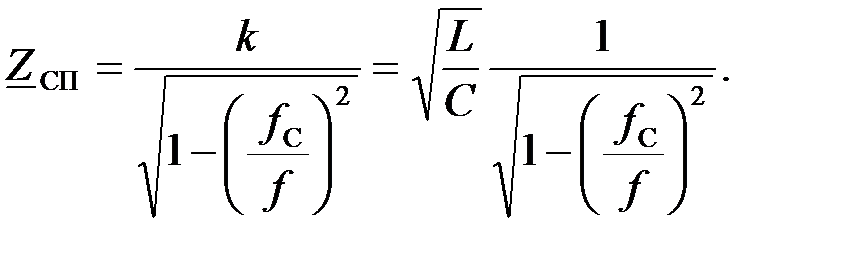
На частоте 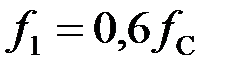 в полосе пропускания характеристическое сопротивление имеет индуктивный характер:
в полосе пропускания характеристическое сопротивление имеет индуктивный характер:
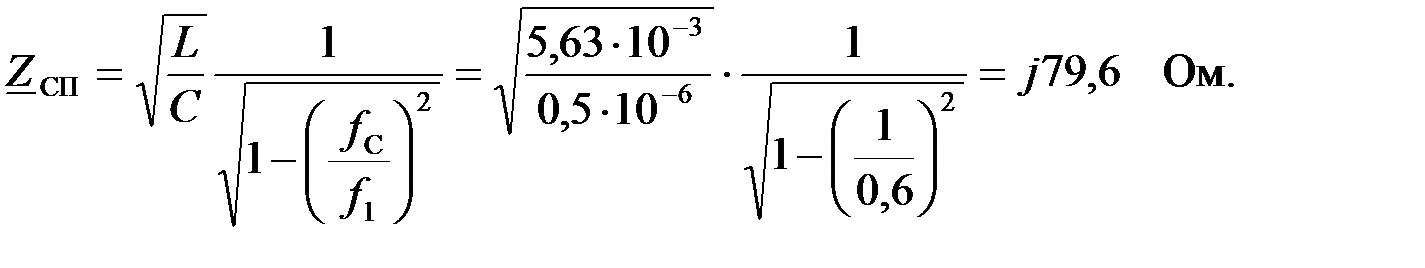
На частоте 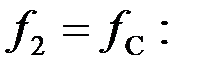
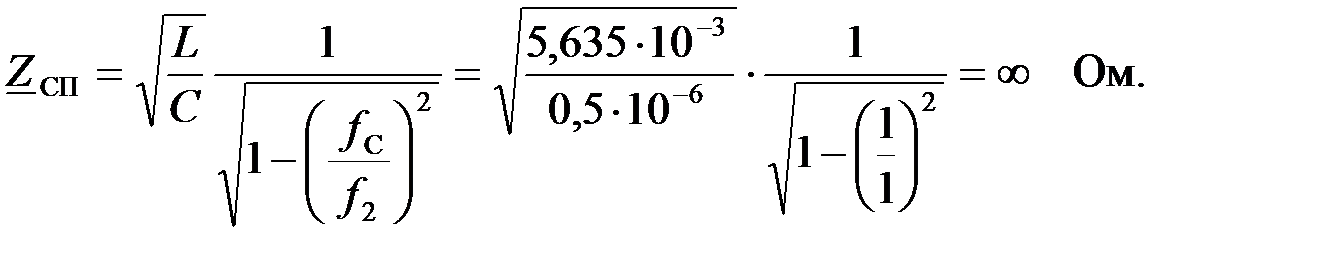
На частоте 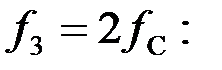
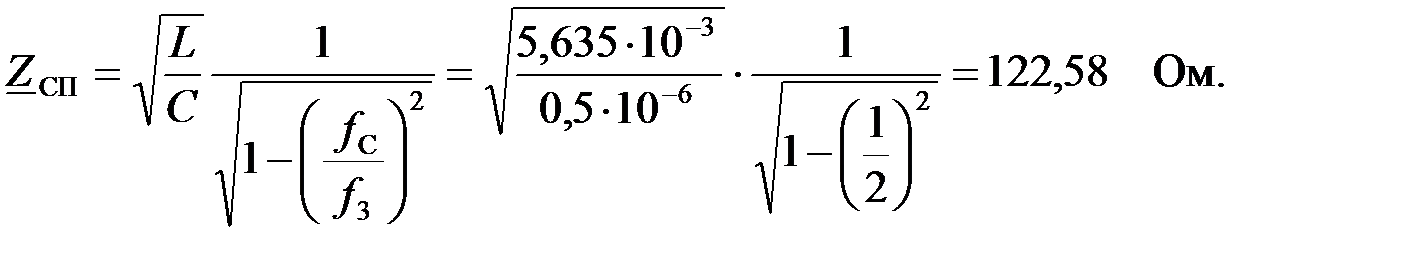
Рассчитаем сопротивления элементов фильтра на частоте 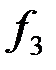 :
:
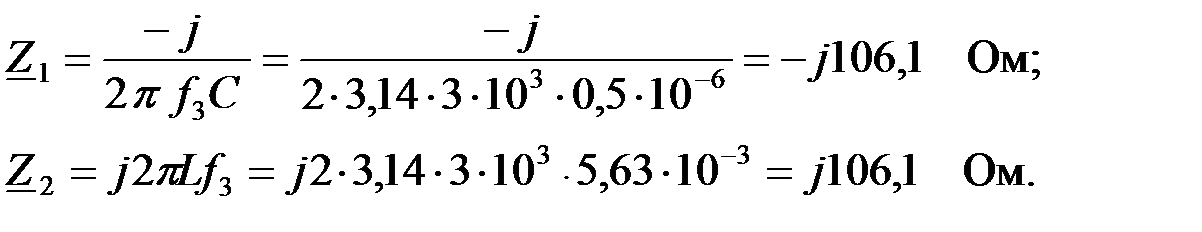
Определим токи и напряжения в элементах фильтра (рис.3.2.6,б) на частоте 
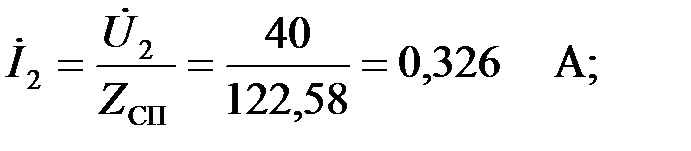
Зная сопротивление 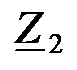 и напряжение и напряжение 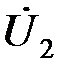 на основании закона Ома, найдем ток на основании закона Ома, найдем ток 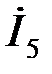 в сопротивлении в сопротивлении 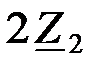
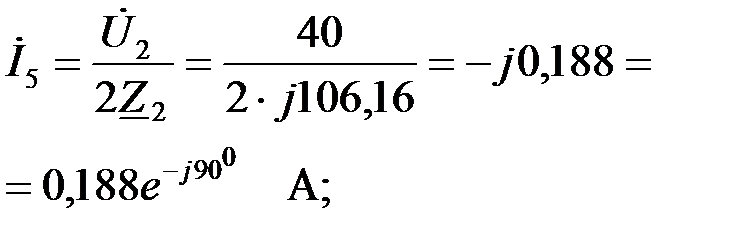
|
В соответствии с пепвым законом Кирхгофа находим ток 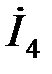
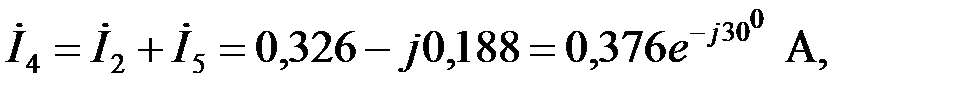
а затем определяем падение напряжения на сопротивлении 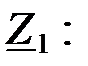
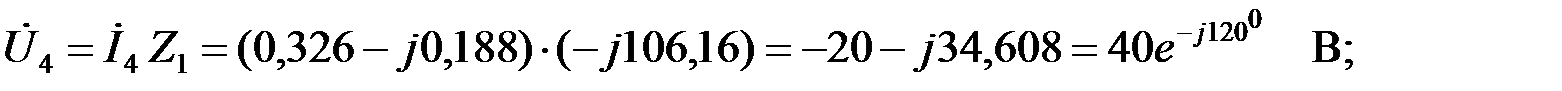
Входное напряжение ФВЧ найдем как сумму падений напряжений на сопротивлениях 
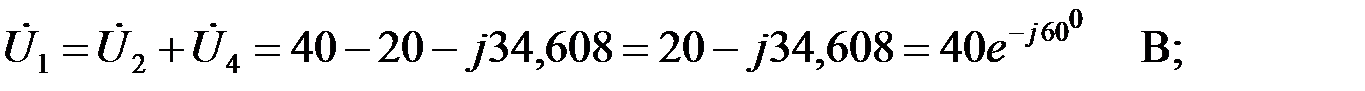
Тогда ток 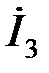 определим в соответствии с законом Ома:
определим в соответствии с законом Ома:
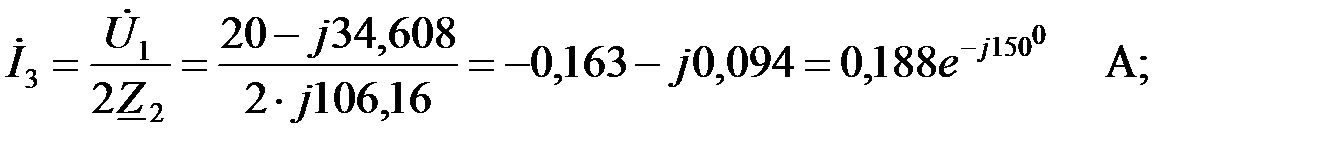
Входной ток ФВЧ вычислим по первому закону Кирхгофа:

Векторная диаграмма токов и напряжений ФВЧ приведена на рис.3.2.6,в.
Рис.3.2.6,в
3.3 Полосовые фильтры типа «k»
Задача 3.3.1. Определить параметры полузвена полосового фильтра типа «k», представленного на рис. 3.3.1, если граничные частоты соответственно равны 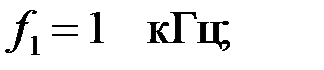
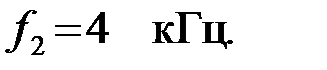 Номинальное волновое сопротивление равно 250 Ом. Определить характеристическое сопротивление и коэффициент фазы
Номинальное волновое сопротивление равно 250 Ом. Определить характеристическое сопротивление и коэффициент фазы 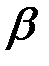 на частоте
на частоте 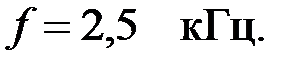
Решение:
Найдем параметры элементов ПФ [8]:
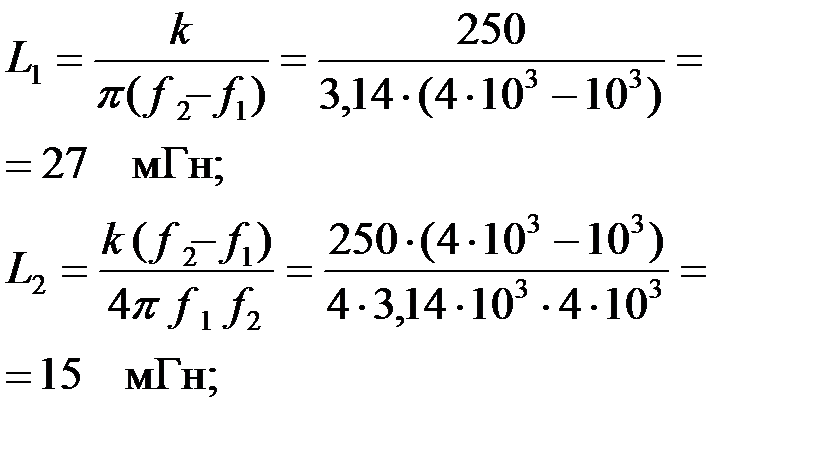
|
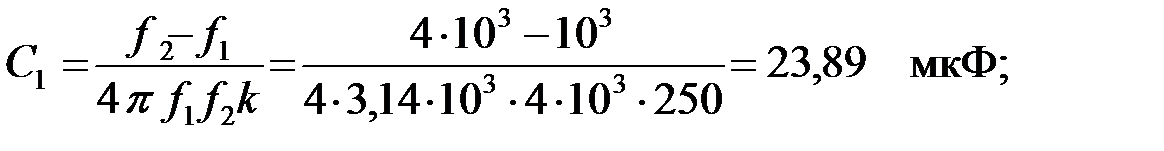
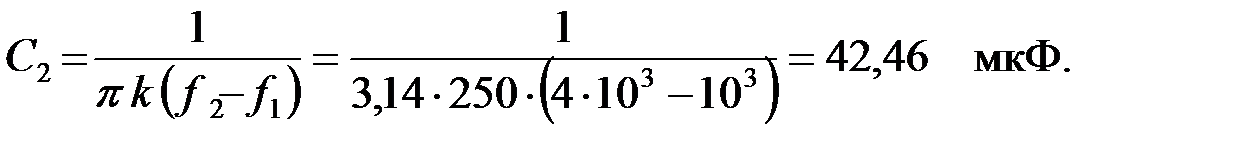
Найдем характеристическое сопротивление на частоте 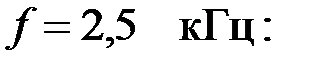
Для этого вначале определим резонасную частоту:
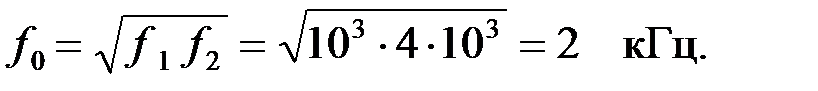
Вычислим нормированную частоту [8]:
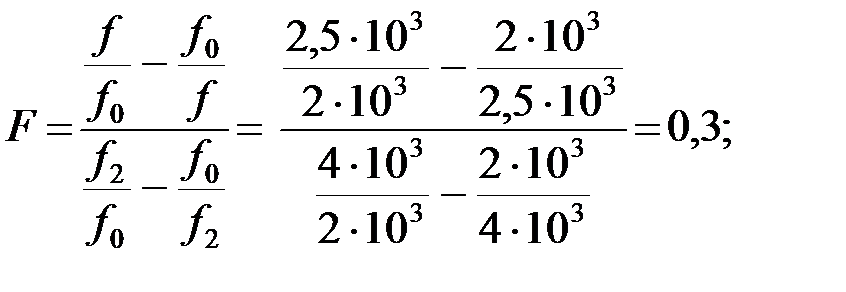
Тогда характеристическое сопротивление:
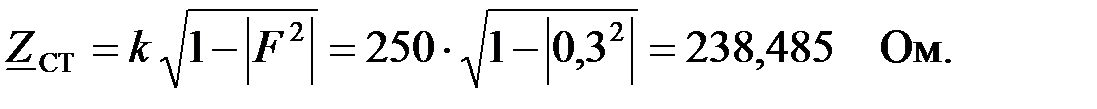
Определим коэффициент фазы 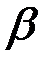 , как:
, как:
Задача 3.3.2 Определить граничные частоты, значение емкостей конденсаторов и коэффициент затухания полосового фильтра (ПФ), представленного на рис. 3.3.2, при частоте 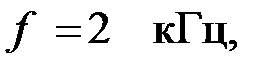 если
если 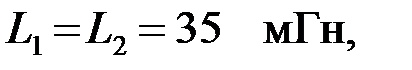 а резонансная частота
а резонансная частота 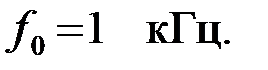
| Решение Так как индуктивности последовательного и параллельного звеньев равны, то это означает, что у симметричного ПФ должны быть равны и емкости конденсаторов. |
Тогда номинальное волновое сопротивление полосового фильтра найдем как:
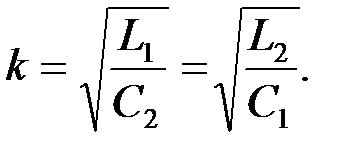
Индуктивности ПФ определяются выражениями [8]:
 а частота:
а частота: 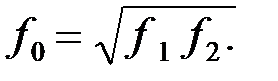
Используя указанные выше соотношения, найдем граничные частоты ПФ 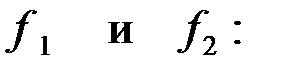
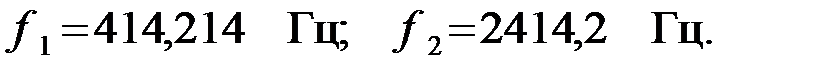
Зная граничные частоты, найдем номинальное волновое сопротивление 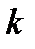 :
:
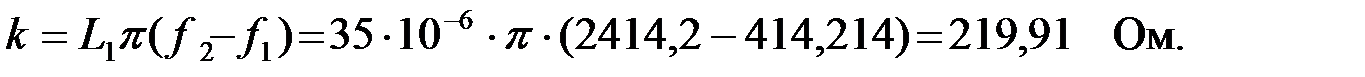
По значениям граничных частот и номинальному волновому сопротивлению найдем емкость конденсаторов:
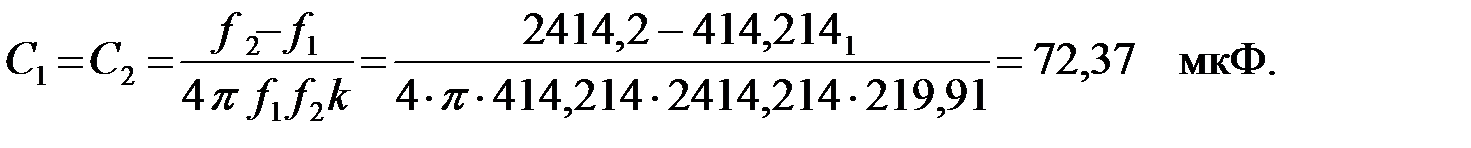
Для определения коэффициента фазы на заданной частоте вычислим нормированную частоту, которая определяется по формуле:
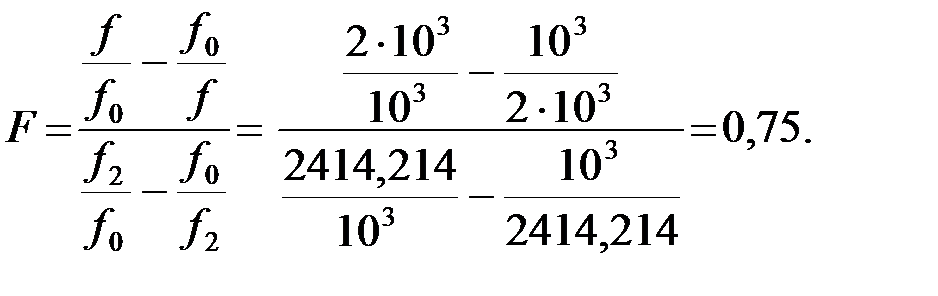
Сигнал заданной частоты находится в полосе пропускания, следовательно, коэффициент фазы ПФ будет равен [8]:
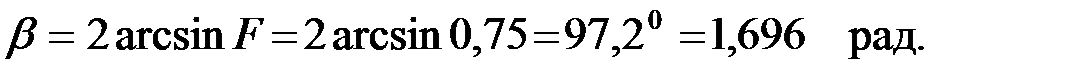
Задача 3.3.3 Определить полосу пропускания ПФ, представленного на рис. 3.3.3, если параметры элементов фильтра равны: 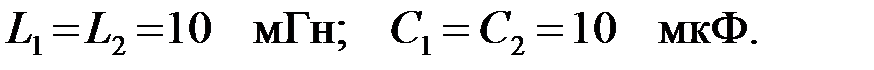
Построить графические зависимости коэффициента затухания a, коэффициента фазы b и характеристического сопротивления  в функции частоты.
в функции частоты.
Решение
Номинальное волновое сопротивление определяется соотношением:
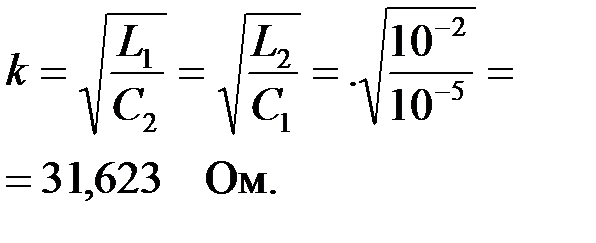
|
Зная параметры фильтра найдем граничные частоты[1]:
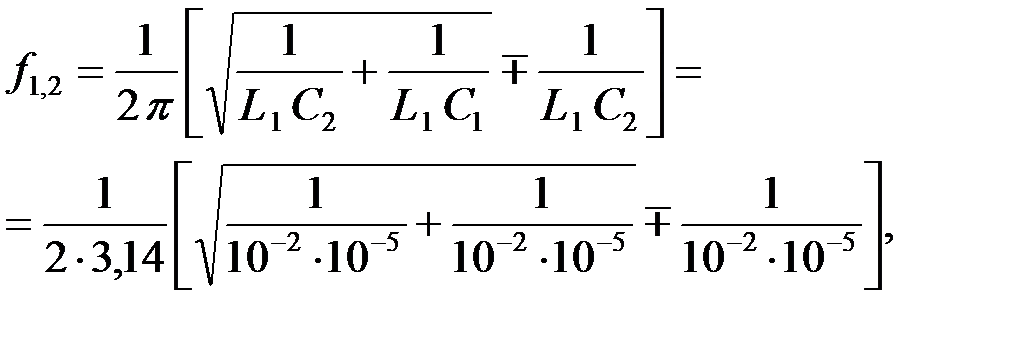
Откуда имеем: 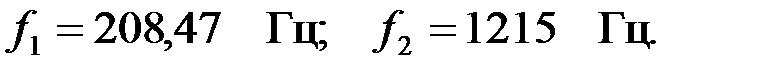
Графические зависимости для полосового фильтра, собранного по П – образной схеме строятся по следующим соотношениям:
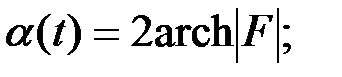 В полосе пропускания:
В полосе пропускания:
 ,
В ролосе затухания: ,
В ролосе затухания:
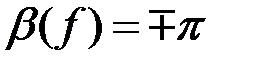
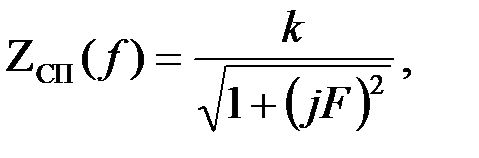 где
где
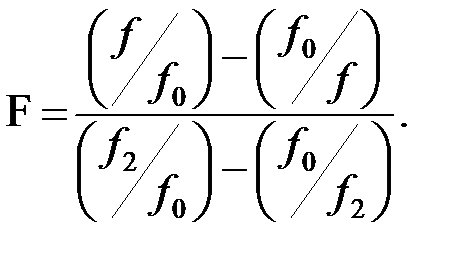
|
Графические зависимости 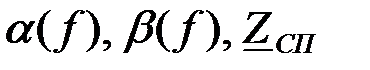 приведены на рис.3.3.3,б.в.г.
приведены на рис.3.3.3,б.в.г.
Задача 3.3.4 Определить характеристическое сопротивление и коэффициент передачи 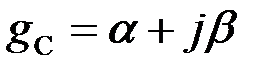 на частоте
на частоте 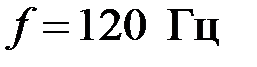 полосового фильтра, собранного по Т – схеме, если параметры его элементов известны:
полосового фильтра, собранного по Т – схеме, если параметры его элементов известны: 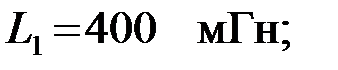
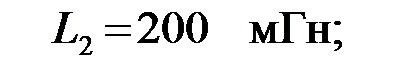
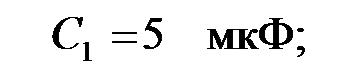
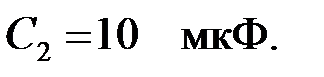 Рассчитать токи и напряжения на элементах фильтра, если входное напряжение
Рассчитать токи и напряжения на элементах фильтра, если входное напряжение 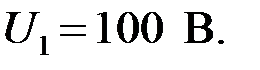 Построить векторную диаграмму токов и падений напряжений, а также графические зависимости коэффициента затухания «a», коэффициента фазы «b» и характеристического сопротивления в функции частоты.
Построить векторную диаграмму токов и падений напряжений, а также графические зависимости коэффициента затухания «a», коэффициента фазы «b» и характеристического сопротивления в функции частоты.
Решение
Схема полосового фильтра, собранного по Т – образной схеме приведена на рис.3.3.4,а.
Найдем граничные частоты полосового фильтра[8]:
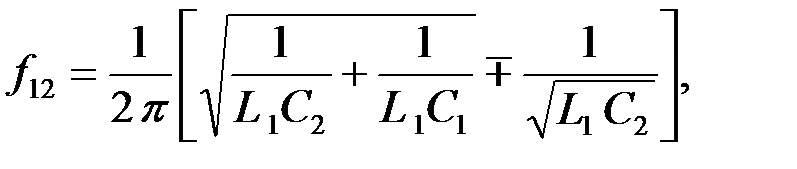 откуда откуда
|

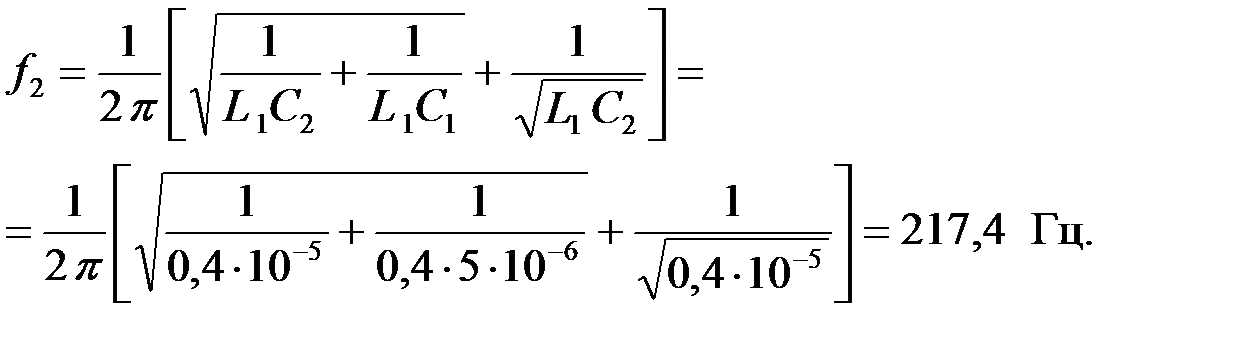
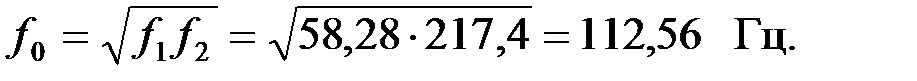
Для определения коэффициента фазы «β» и характеристического волнового сопротивления «k» на заданной частоте вычислим вначале нормированную частоту F, которая определяется по формуле:
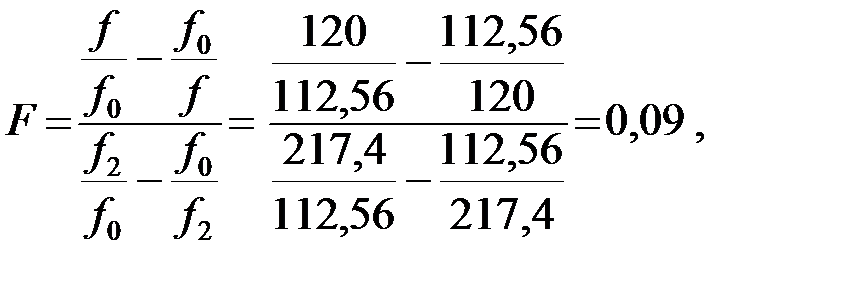 тогда
тогда
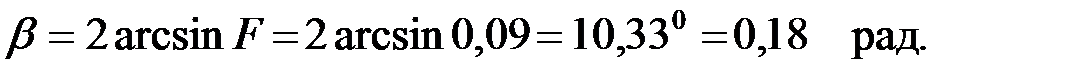
Для того чтобы определить характеристическое сопротивление 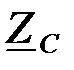 ПФ через параметры фильтра, вычислим номинальное характеристическое волновое сопротивление:
ПФ через параметры фильтра, вычислим номинальное характеристическое волновое сопротивление:
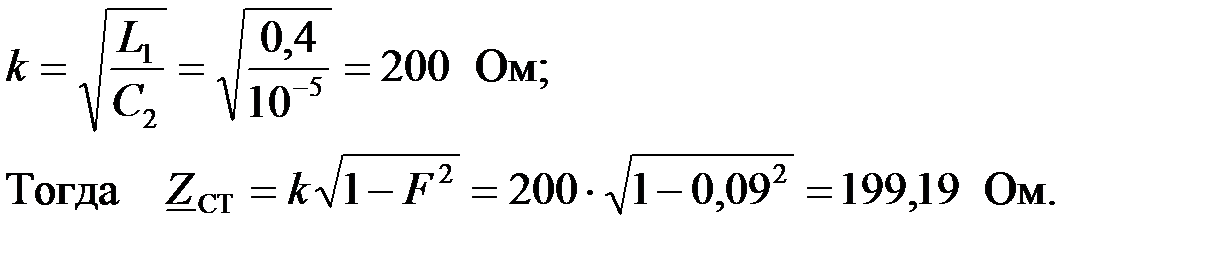
Для определения токов и напряжений, а также построения векторной диаграммы, рассчитаем сопротивления звеньев фильтра на заданной частоте 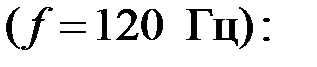
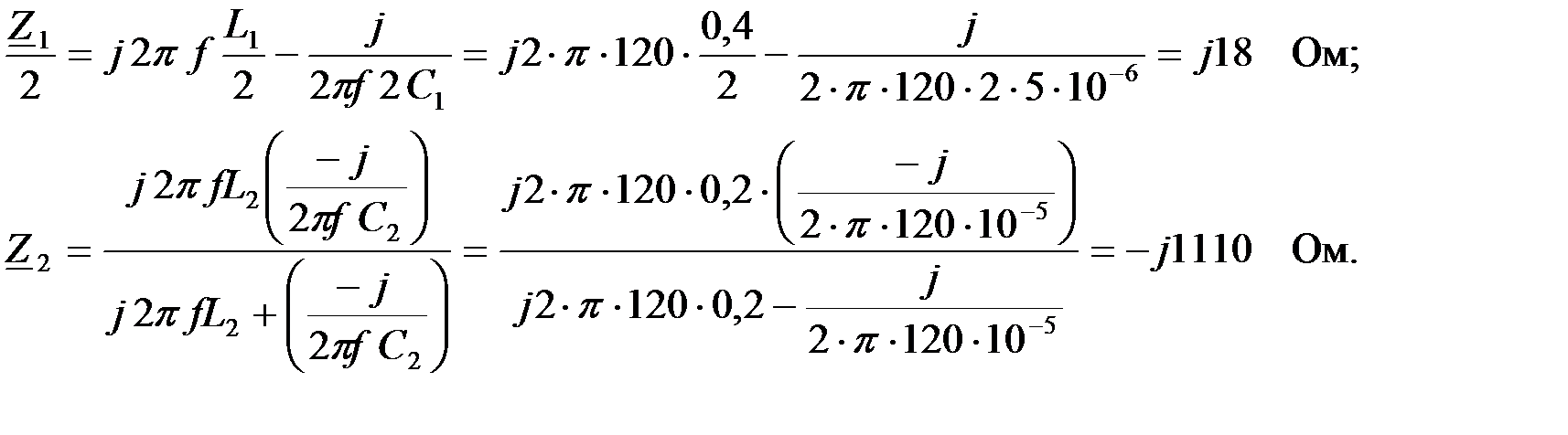 Схема замещения фильтра приведена на рис.3.3.4,б
Схема замещения фильтра приведена на рис.3.3.4,б
Используя схему замещения, найдем входной ток ПФ 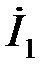 :
:
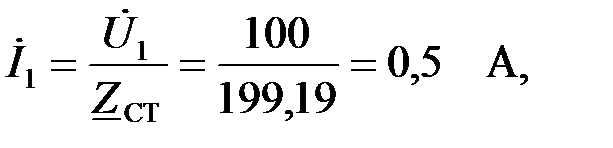
а затем вычислимпадения напряжений на входном последовательном и параллельном сопротивлениеях:
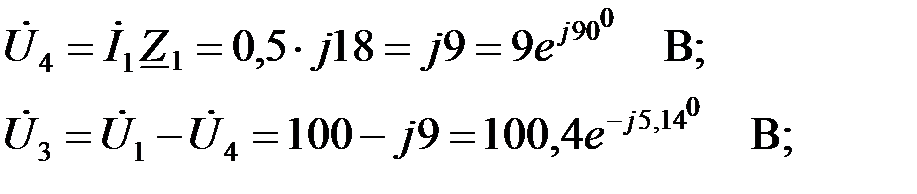 Определим ток в параллельном сопротивлении:
Определим ток в параллельном сопротивлении:
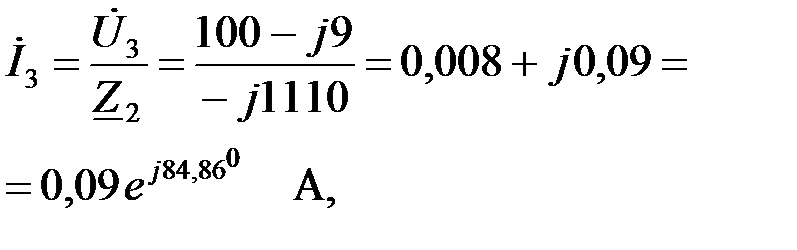
|
а затем, по первому закону Кирхгофа ток 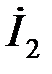 – на выходе ПФ:
– на выходе ПФ:

После чего рассчитаем напряжение на выходе ПФ:
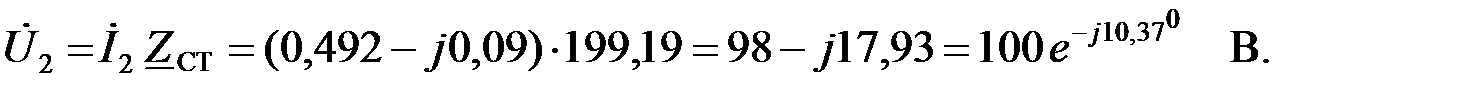
Векторная диаграмма токов и напряжений приведена на рис.3.3.4,в
Рис.3.3.4,в
На рис.3.3.4,г,д,е показаны графические зависимости коэффициента затухания « », коэффициента фазы «
», коэффициента фазы « », и характеристического сопротивления
», и характеристического сопротивления 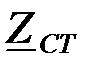 в функции угловой частоты.
в функции угловой частоты.
 Рис.3.3.4,ж
Рис.3.3.4,ж

Задача 3.3.5 Определить полосу пропускания ПФ, собранного по П – образной схеме и его характеристические параметры на частоте 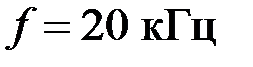 , если параметры его элементов известны:
, если параметры его элементов известны: 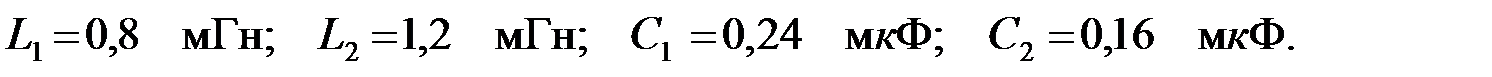 Рассчитать токи и напряжения в звеньях фильтра, если известно входное напряжение
Рассчитать токи и напряжения в звеньях фильтра, если известно входное напряжение  Построить векторную диаграмму токов и напряжений, а также графические зависимости коэффициента затухания
Построить векторную диаграмму токов и напряжений, а также графические зависимости коэффициента затухания 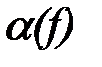 , коэффициента фазы
, коэффициента фазы 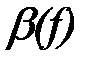 , и характеристического сопротивления
, и характеристического сопротивления 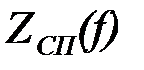 в функции частоты.
в функции частоты.
| Решение Полосовой фильтр, собранный по П – образной схеме представлен на рис.3.3.5,а. |
Определим номинальное волновое сопротивление полосового фильтра:
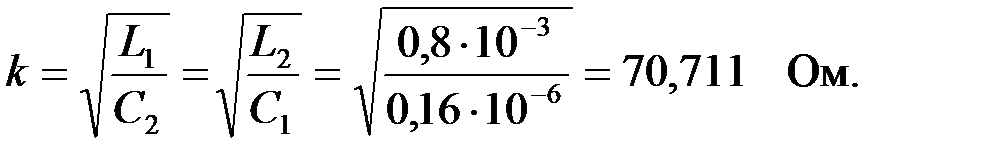
Рассчитаем граничные частоты полосового фильтра в соответствии с выражением:
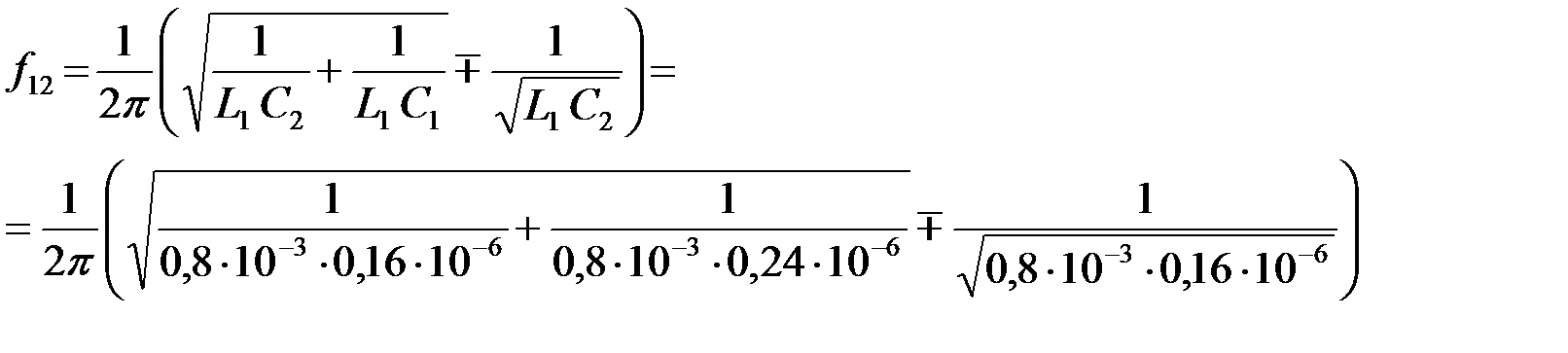
Откуда находим: 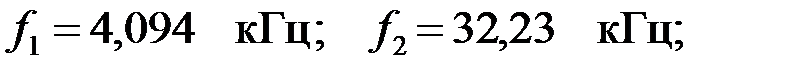
Собственная резонансная частота ПФ определяется как:
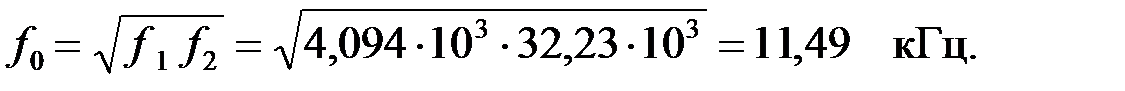
Вычислим нормированную частоту F на заданной частоте:
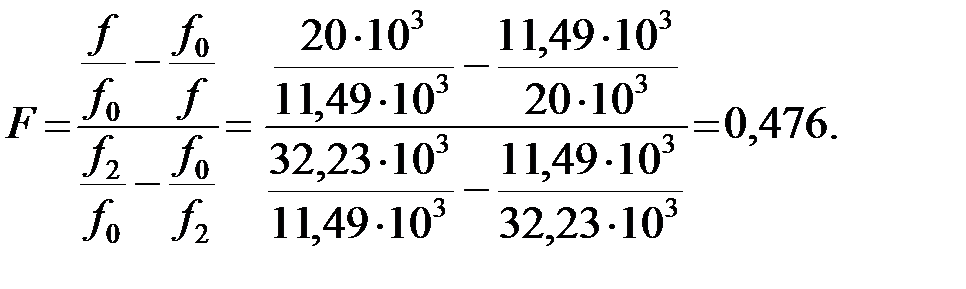
Тогда характеристическое сопротивление ПФ:

Определим коэффициент фазы:
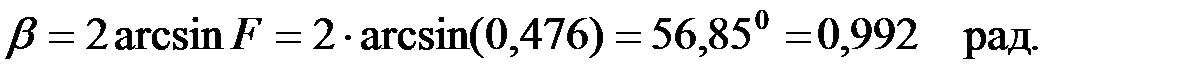
Схема замещения ПФ для определения токов и напряжений, а также построения векторной диаграммы показана на рис.3.3.5,б. Определим комплексные сопротивления звеньев фильтра на заданной частоте:
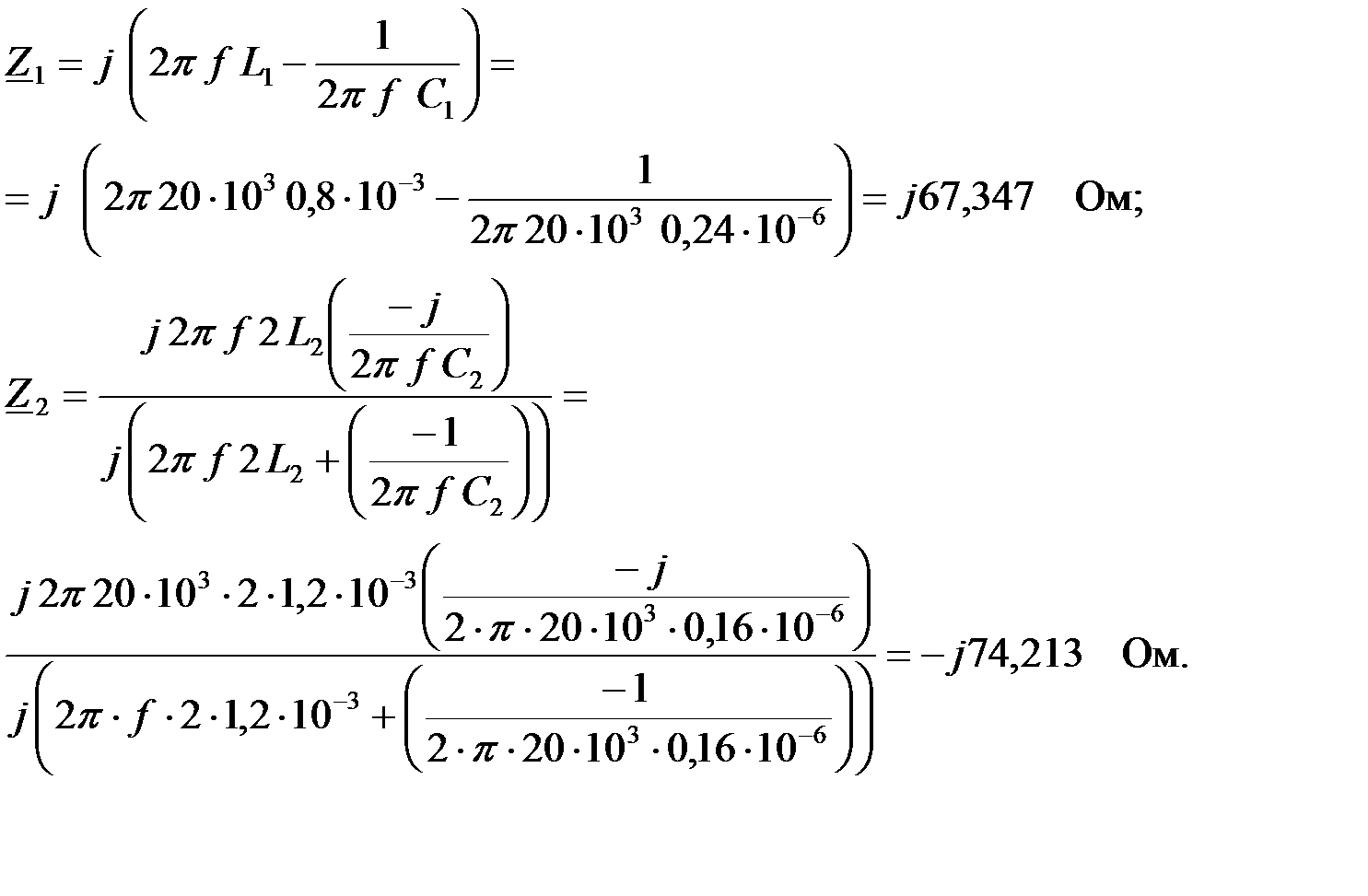
Дата добавления: 2015-10-21; просмотров: 105 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ 1 страница | | | ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ 3 страница |