Результат неверного истолкования эксперимента

Первые опыты, которые, казалось бы, определяли характер изменения массы - в зависимости от скорости - , были проведены Бухерером, Вольцем и Нейманом. Прибор Неймана схематически изображён на рис. 1.

1 2 3 4

А

В

Рис. 1

Вектор магнитной индукции направлен перпендикулярно плоскости рисунка. К двум параллельным электродам 3, расположенным на расстоянии , подведено напряжение . Радиевый источник 1 испускает электроны с зарядом высокой энергии. Фотопластинка 4 отображает места попадания электронов. В приборе создан вакуум. В отсутствие электрического и магнитного полей электроны пролетающие в отверстие экрана 2 попадают на фотопластинку в точке А (экспозиция равна нескольким часам). Затем накладываются электрическое и магнитное поля. Электрическая и магнитная силы направлены противоположно друг другу, и, следовательно, создаётся селектор скоростей. Любой электрон, проходящий через селектор, должен иметь относительно прибора скорость (3.6.1)

После того как электроны выходят из селектора скоростей, они оказываются под действием одной лишь постоянной магнитной силы, равной

(3.6.2)

и направленной перпендикулярно к скорости . Поэтому ускорение постоянно по величине и направлено перпендикулярно к . Где - масса электрона. Как раз при этом условии орбита электрона представляет собой дугу окружности. Движение по окружности радиуса требует наличия центростремительного ускорения , постоянного по величине и всюду перпендикулярного траектории. Следовательно,

(3.6.3)

Откуда (3.6.4)

Измеряя , и , находим из (3.6.1). Подставив значения, , и в (3.6.4) определим радиус . Однако эксперименты показали, чем больше подавалось напряжение и накладывалось магнитное поле, то есть, чем с большей скоростью селектировались электроны, тем больше становился радиус отклонения электронов в экспериментах от теоретически расчётного. Создавалось впечатление, что масса электрона начинает стремительно возрастать с увеличением скорости. Этим обстоятельством и воспользовались релятивисты, введя поправочный множитель 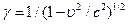в уравнение (4) для оправдания теории относительности. (Описание эксперимента взято из книги «Современная физика». Р. Спроул, М. 1974)

Рассмотрим тот же эксперимент с применением результатов исследования фарадеево-максвелловских механических моделей взаимодействия.

Перепишем уравнения (2.4.3) и (2.4.4), заменяя значение обильности на величину зарядов в соответствии с (3.1.1) и (3.1.2).

= + (3.6.5)

= (3.6.6)

Тогда на отрицательно заряженный электрон (сток), движущийся между заряженными пластинами будет действовать суммарные силы.Сверху силы притяжения от распределённых по поверхности пластины положительных зарядов. Снизу, от распределённых по поверхности пластины отрицательных зарядов. Приняв за положительное направление, направлениеот нижней пластины к верхней, получим суммарную силу, действующую на электрон.

+ (3.6.7)

Где 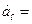- так как последние совпадают по величине и направлению.

Первое слагаемое, как было показано в (3.1) равно распределённой электростатической силе . Где . Второе слагаемое представляет собой динамическую составляющую сил, действующих на электрон, пропорциональную заряду электрона и его ускорению в направлении от нижней заряженной пластины к верхней. Тогда уравнение (3.6.7) примет вид

(3.6.8)

Величина этой силы, как и в предыдущих рассуждениях, должна быть уравновешена магнитной силой. То есть

= (3.6.9)

Откуда (3.6.10)

Подставляя значение (3.6.10) в (3.6.4), получим

(3.6.11)

Дата добавления: 2015-10-13