Шаровых изолированных источников и стоков

Рассмотрим общеизвестную классическую фарадеево-максвелловскую постановку

задачи взаимодействия двух шаровых объектов, излучающих и поглощающих материальные частицы. Объекты, излучающие материальные частицы назовём источниками, а поглощающие – стоками. На рисунках (рис. 1) и (рис. 2) изображены схемы механических моделей взаимодействия источников и стоков. Линии тока определяют траектории движения потоков частиц.

источник – сток

(рис. 1)

источник – источник

(рис. 2)

Конфигурация расположения линий тока частиц в случае взаимодействия сток –

сток будет аналогична конфигурации взаимодействия источник – источник (рис. 2). Отличие заключается в том, что линии тока в этом случае будут направлены к стокам.

Выделим изолированную материальную систему, состоящую из шарового

источника, ограниченного поверхностью радиуса , и пространства, равномерно заполненного частицами.

Предположим, что источник характеризуется постоянной обильностью - , то есть

постоянным массовым расходом частиц в единицу времени, проходящих через его поверхность. Тогда, принимая за положительное, направление от центра источника, получим:

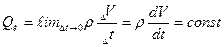(3.1.1)

Где:

- плотность частиц в единице объёма;

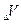- приращение объёма;

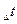- приращение времени.

Приращение объёма определим как разность объёмов сфер. Сферы, ограничивающей фронт частиц излученных источником за время 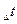, радиусом и сферы, ограничивающей источник, радиусом (рис. 3).

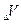
рис. 3

(3.1.2)

Определим производную функции V в зависимости отаргумента R:

= (3.1.3)

Подставляя полученное значение dV из (3.1.3) в уравнение (2.1.1), получим зависимость:

dt = (3.1.4)

Из (3.1.4) определим поле распределения скоростей частиц изолированного источника в зависимости от расстояния.

(3.1.5)

Аналогично определим поле распределения скоростей частиц изолированного стока:

(3.1.6)

Где: – обильность стока.

Продифференцировав скорости частиц в (3.1.5) и (3.1.6) по времени (3.1.4),

определим поля распределения ускорений частиц изолированного источника и стока, соответственно:

(3.1.7)

(3.1.8)

Где: и - ускорения частиц источника и стока соответственно.

Дата добавления: 2015-10-13