Взаимодействие двух неподвижных шаровых объектов

Рассмотрим два материальных объекта: I (источник) и II (сток), ограниченных поверхностями сфер радиусов и , соответственно (рис. 4). Выделим на сфере объекта I элемент поверхности (кольцо), заключённый между сечениями образованными двумя соосными конусами, образующими угол . Вершины конусов находятся в центре сферы радиуса , а направление осей совпадает с единичным вектором .

объект I (источник) объект II (сток)

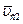
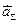
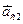
Рис. 4

Где: – расстояние между центрами объектов I и II;

- орт направления от центра объекта I к центру объекта II;
– орт внешней нормали к элементу поверхности ;

– угол между ортом и ортом ;

– приращение угла ;

- угол между отрезком, соединяющим поверхность с центром объекта II и

направлением орта ;

- скорость частиц, излучаемых объектом I c поверхности Δs;

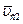– скорость частиц поглощаемых объектом II с поверхности Δs;

- ускорение частиц, излучаемых объектом I с поверхности ;

- ускорение частиц, поглощаемых объектом II с поверхности ;

-модуль суммарной скорости частиц в проекции на орт ;

- суммарное ускорение частиц;

;

Или, переходя к пределу:

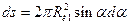. (3.3.1)

Вариант I

Применяя принцип суперпозиции для полей скоростей и ускорений частиц, определим выражение для проекции силы, действующей на источник I в направлении при взаимодействии со стоком II:

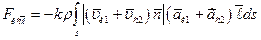(3.3.2)

Подставляя в (3.3.2) значения ds из (2.3.1) для случая , получим:

(3.3.3)

Для достаточно больших расстояний между взаимодействующими объектами, когда 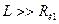, угол стремится к нулю, к единице, и расстояние от центра объекта II до элемента поверхности стремится к , получим:

=

= =

=

= 2 (3.3.4)

Подставляя в (3.3.4) ранее полученные значения из (3.1.5) - (3.1.8), определим выражение для проекции силы, действующей на источник I в направлении при взаимодействии со стоком II:

источник I – сток II

(3.3.5)

Аналогично получим выражения для сил, действующих на объект I в случаях:

источник I – источник II

(3.3.6)

сток I – источник II

(3.3.7)

сток I – сток II

(3.3.8)

Предположим, что обильности источников и стоков прямопропорциональны их массам:

(3.3.9)

(3.3.10)

Где: 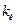и – коэффициенты пропорциональности масс источника - и стока - соответственно;

и - плотность объектов – источника и стока соответственно;

и - радиусы объектов – источника и стока соответственно.

Заменяя один из сомножителей в уравнениях (3.3.5) – (3.3.8) на его значение из (3.3.9) и (3.3.10) и, поменяв слагаемые местами, получим:

источник I – сток II

= (3.3.11)

источник I - источник II

= (3.3.12)

cток I – источник II

= (3.3.13)

cток I – сток II

= (3.3.14)

На рис. 5 и 6 представлены характеристики графиков зависимости сил, действующих на объект I, в зависимости от расстояний между объектами.

рис. 5 рис. 6

Вариант II

Решение задачи взаимодействия двух шаровых объектов можно получить и с применением уравнения Бернулли. Используем ранее введенные обозначения. Тогда, сила , действующая на объект I в направлении , будет равна:

(3.3.14)

Где: - const.

Знак (-) перед интегралом указывает на то, что направление распределённых сил давления на элемент поверхности противоположен выбранному направлению .

Для достаточно больших расстояний между взаимодействующими объектами, когда , угол стремится к нулю, к единице, и расстояние от центра объекта II до элемента поверхности стремится к L получим:

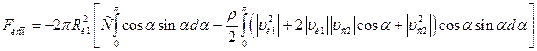(3.3.15)

Где:

= (3.3.16)

=

= (3.3.18)

Подставляя в (3.3.18) значения (3.1.5) и (3.1.6), получим окончательно:

источник I – сток II

(3.3.19)

Аналогично получим выражения для сил, действующих на объект I в случаях:

источник I – источник II

(3.3.20)

cток I – источник II

(3.3.21)

cток I – сток II

(3.3.22)

Резюме.

Уравнения (3.3.10) - (3.3.13) идентичны уравнениям (3.3.19) - (3.3.22). Результаты аналитического исследования взаимодействия двух неподвижных шаровых объектов устанавливают, что силы взаимодействия отличаются от законов обратной пропорциональности квадратам расстояний на небольших расстояниях между объектами.

Из этого следует, что законы обратной пропорциональности квадратам расстояния между взаимодействующими объектами являются частными случаями трёх основных законов Ньютона.

Однако следует отметить, что все наши собственные физические модели в силу принятых абстракций, допущений и ограничений являются лишь приближением к действительности. В связи с этим предпочтение следует отдавать тем моделям, которые наиболее полно подтверждаются опытом.

Дата добавления: 2015-10-13